In this article, we shall study to write vector and cartesian equation of a line in Space.
Theorem – 1 (Vector Equation of Line in Space):
The vector equation of a straight line passing through a fixed point with position vector a and parallel to a given vector b is r = a + λ b. Where λ is scalar and called the parameter.
Notes:
- In the above equation r is a position vector of any point P(x, y, z) on the line, then r = x
 + y
+ y  + z
+ z 
- The position vector of any point on the line is taken as a + λ b. This form of the equation is called the vector form.
- If the line passes through the origin its vector equation is r = λ b
- The vector equation of a line passing through a fixed point with position vector a and parallel to a given vector b is also given as
(r – a) × b
Theorem – 2 (Cartesian Equation of Line in Space):
The cartesian equation of a straight line passing through a fixed point P(x1, y1, z1) and having direction ratios (d.r.s) proportional to a, b, c respectively is given by
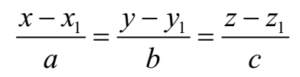
Notes:
- If
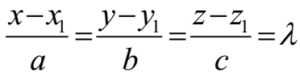 then x = aλ + x1, y = bλ + y1, and z = cλ + z1. These equations are called the parametric equations of the line.
then x = aλ + x1, y = bλ + y1, and z = cλ + z1. These equations are called the parametric equations of the line. - The coordinates of any point on the line are (aλ + x1, bλ + y1, cλ + z1).
- If the line passes through the origin its equation is
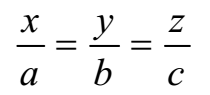
- Since the direction cosines (d.c.s) of a line are direction ratios (d.r.s) of the line, the equation of the line passing through a fixed point P(x1, y1, z1) and having direction cosines (d.c.s) l, m, n respectively is given by
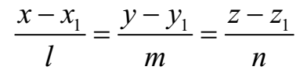
- The x-axis, y-axis, and z-axis pass through origin.
- d.r.s of x-axis are 1, 0, 0. Hence its equation is y = 0 and z = 0.
- d.r.s ofy-axiss are 0, 1, 0. Hence its equation is x = 0 and z = 0.
- d.r.s of z – axis are 0, 0, 1. Hence its equation is x = 0 and y = 0.
Theorem – 3:
The vector equation of a straight line passing through two fixed points with position vector a and b is
r = a + λ( b – a)
Where λ is scalar and called the parameter.
Theorem – 4:
The cartesian equation of a straight line passing through two fixed points P(x1, y1, z1) and Q(x2, y2, z2) is given by
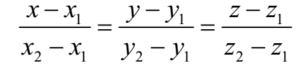
To find Direction Ratios and Direction Cosines of Line in Space:
Algorithm:
- Write the equation in standard form
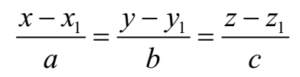
- Make sure there are no coefficients for the x, y, and z terms. If coefficients are present divide the numerator and denominator by the coefficient.
- Do simplification if any
- Then the denominators indicate the direction ratios.
- Using direction ratios, find direction cosines
Example 01:
- Find the direction cosines of the line
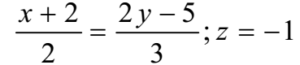
- Solution:
The equation of the line is
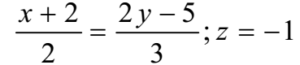
Writing in a standard form
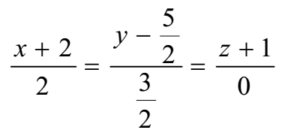
The d.r.s of lines are 2, 3/2, 0 i.e. 4, 3, 0 ≡ a, b, c
Now d.c. s of the line are
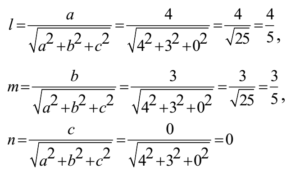
Ans: d.c.s of the line are 4/5, 3/5, 0
Example 02:
- Find the direction cosines of the line
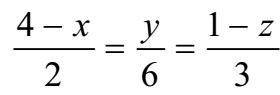
- Solution:
The equation of the line is
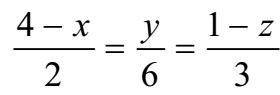
Writing in a standard form
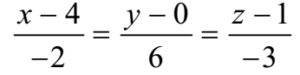
The d.r.s of lines are -2, 6, -3 ≡ a, b, c
Now d.c. s of the line are
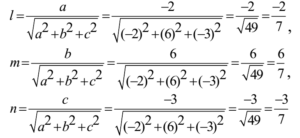
Ans: d.c.s of the line are -2/7, 6/7, -3/7
Example 03:
- Find the direction cosines of the line
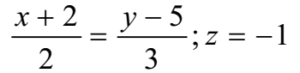
- Solution:
The equation of the line is
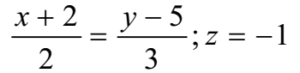
Writing in a standard form
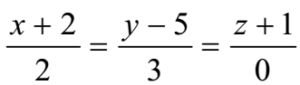
The d.r.s of lines are 2, 3, 0 ≡ a, b, c
Now d.c. s of the line are
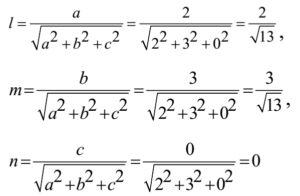
Ans: d.c.s of the line are 2/√13, 3/√13, 0.
Example 04:
- Find the direction cosines of the line
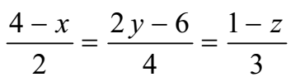
- Solution:
The equation of the line is
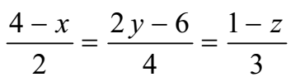
Writing in a standard form
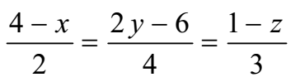
The d.r.s of lines are 2, 4, 3 ≡ a, b, c
Now d.c. s of the line are
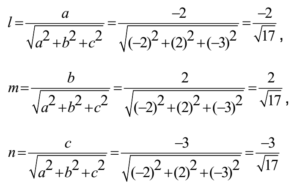
Ans: d.c.s of the line are -2/√17, 2/√17, -3/√17.
Conversion of Vector Equation into Cartesian Equation of Line in Space:
Algorithm:
- Equate the vector form r = a + λ b to r = x
 + y
+ y  + z
+ z 
- Open the brackets of R.H.S.
- Group the terms of
 ,
,  , and
, and 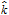
- Equate corresponding terms on both the sides
- Find three distinct equations for λ.
- Equate the three equations
Example 05:
- Find the cartesian equations of a line whose vector equation is r = (2
 –
–  + 4
+ 4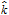 ) + λ(
) + λ(  +
+  – 2
– 2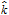 )
) - Solution:
The vector equation of the line is
r = (2 ![]() –
– ![]() + 4
+ 4![]() ) + λ(
) + λ( ![]() +
+ ![]() – 2
– 2![]() )
)
Where, r = x ![]() + y
+ y ![]() + z
+ z ![]()
∴ x ![]() + y
+ y ![]() + z
+ z ![]() = (2
= (2 ![]() –
– ![]() + 4
+ 4![]() ) + λ(
) + λ( ![]() +
+ ![]() – 2
– 2![]() )
)
∴ x ![]() + y
+ y ![]() + z
+ z ![]() = 2
= 2 ![]() –
– ![]() + 4
+ 4![]() + λ
+ λ![]() + λ
+ λ![]() – 2λ
– 2λ![]()
∴ x ![]() + y
+ y ![]() + z
+ z ![]() = (2 + λ)
= (2 + λ) ![]() + (-1 + λ)
+ (-1 + λ) ![]() + (4 – 2 λ)
+ (4 – 2 λ)![]()
∴ x = 2 + λ ⇒ λ = x – 2 …………. (1)
∴ y = -1 + λ ⇒ λ = y + 1 …………. (2)
∴ z = 4 – 2λ ⇒ λ = (z – 4)/(-2) …………. (3)
From equations (1), (2) and (3)
x – 2 = y + 1 = (z – 4)/(-2)
Thus the cartesian equations of lines are
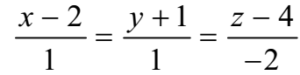
Conversion of Cartesian Equation into Vector Equation of Line in Space:
Algorithm (Method – I):
- Write given the cartesian equation in standard form.
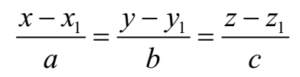
- Then write the position vector of the point through which the line is passing. a = x1
 + y1
+ y1 + z1
+ z1
- The direction ratios of the line are a, b, and c. Write the direction vector, b = a
 + b
+ b  + c
+ c 
- Write the vector form of the equation as r = a + λ b. Where λ ∈ R, and is a scalar/parameter
- Thus vector equation of line is r = (x1
 + y1
+ y1 + z1
+ z1 )+ λ (a
)+ λ (a  + b
+ b  + c
+ c  )
)
Algorithm (Method – II):
- Let
- Find x = aλ + x1, y = bλ + y1, and z = cλ + z1,
- Substitute values of a, y, and z in the equation r = x
 + y
+ y  + z
+ z 
- Group terms on R.H.S without λ and with λ.
- Get the vector equation in the format r = (x1
 + y1
+ y1 + z1
+ z1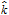 )+ λ (a
)+ λ (a  + b
+ b  + c
+ c 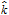 )
)
Example 06:
- Find the vector equation of a line whose cartesian equation is 6x – 2 = 3y + 1 = 2z – 2
- Solution (Method – I):
The cartesian equation of the line is
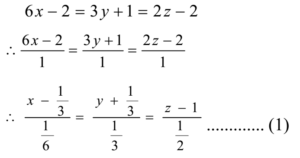
Thus the line passes through the point (1/3, -1/3, 2)
The position vector of this point is a =(1/3)![]() – (1/3)
– (1/3)![]() + 2
+ 2![]()
The d.r. s of the line are i.e. 1, 2, 3 ≡ a, b, c
Hence, the direction vector of the line is b = ![]() + 2
+ 2![]() + 3
+ 3![]()
Now, the vector form of the equation of the line is given by
r = a + λ b
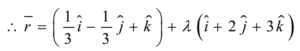
Where λ ∈ R, and is a scalar/parameter
Example 07:
- Find the vector equation of a line whose cartesian equation is
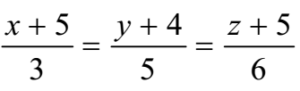
- Solution (Method – II):
The equation of the line is
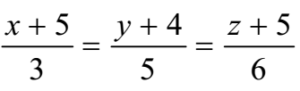
Let, ![]() = λ
= λ
Thus x = 3λ – 5, y = 5λ – 4 and z = 6λ – 5
Now, r = x ![]() + y
+ y ![]() + z
+ z ![]()
r = (3λ – 5) ![]() + (5λ – 4)
+ (5λ – 4) ![]() + (6λ – 5)
+ (6λ – 5) ![]()
r = 3λ ![]() – 5
– 5 ![]() + 5λ
+ 5λ ![]() – 4
– 4 ![]() + 6λ
+ 6λ ![]() – 5
– 5 ![]()
r = – 5 ![]() – 4
– 4 ![]() – 5
– 5 ![]() + 3λ
+ 3λ ![]() + 5λ
+ 5λ ![]() + 6λ
+ 6λ ![]()
r = (- 5 ![]() – 4
– 4 ![]() – 5
– 5 ![]() ) + λ(3
) + λ(3![]() + 5
+ 5![]() + 6
+ 6 ![]() )
)
Where λ ∈ R, and is a scalar/parameter
Example 08:
- Find the vector equation of a line whose cartesian equation is
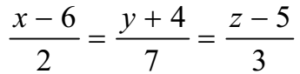
- Solution:
The equation of the line is
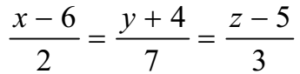
Thus the line passes through the point (6, -4, 5)
The position vector of this point is a = 6![]() – 4
– 4![]() + 5
+ 5![]()
The d.r. s of the line are 2, 7, 3≡ a, b, c
Hence, the direction vector of the line is b = 2![]() + 7
+ 7![]() + 3
+ 3![]()
Now, the vector form of the equation of the line is given by
r = a + λ b
r = (6![]() – 4
– 4![]() + 5
+ 5![]() ) + λ (2
) + λ (2![]() + 7
+ 7![]() + 3
+ 3![]() )
)
Where λ ∈ R, and is a scalar/parameter
Example 09:
- Find the vector equation of a line whose cartesian equation is
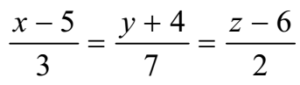
- Solution:
The cartesian equation of the line is
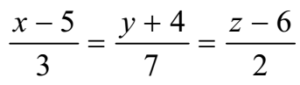
Thus the line passes through the point (5, -4, 6)
The position vector of this point is a = 5![]() – 4
– 4![]() + 6
+ 6![]()
The d.r. s of the line are 3, 7, 2 ≡ a, b, c
Hence, the direction vector of the line is b = 3![]() + 7
+ 7![]() + 2
+ 2![]()
Now, the vector form of the equation of the line is given by
r = a + λ b
r = (5![]() – 4
– 4![]() + 6
+ 6![]() ) + λ (3
) + λ (3![]() + 7
+ 7![]() + 2
+ 2![]() )
)
Where λ ∈ R, and is a scalar/parameter
Example 10:
- Find the vector equation of a line whose cartesian equation is x = ay + b and z = cy + d . Find its direction ratios.
- Solution:
The cartesian equation of the line is
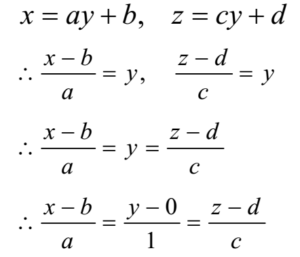
Thus the line passes through the point(b, 0, d)
The position vector of this point is a = b![]() + 0
+ 0![]() + d
+ d![]() = b
= b![]() + d
+ d![]()
The d.r. s of the line are a, 1, c ≡ a, b, c
Hence, the direction vector of the line is b = a![]() +
+ ![]() + c
+ c![]()
Now, the vector form of the equation of the line is given by
r = a + λ b
r = (b![]() + d
+ d![]() ) + λ (a
) + λ (a![]() +
+ ![]() + c
+ c![]() )
)
Where λ ∈ R, and is a scalar/parameter
Example 11:
- Find the vector equation of a line whose cartesian equation is 3x + 1 = 6y – 2 = 1- z . Find the fixed point through which it passes and its. d.r.s
- Solution:
The equation of the line is 3x + 1 = 6y – 2 = 1- z
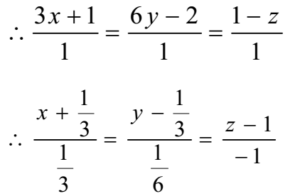
Thus the line passes through the point ( -1/3, 1/3, 1)
The position vector of this point is a = (-1/3)![]() + (1/3)
+ (1/3)![]() +
+ ![]()
The d.r. s of the line are i.e. 1/3, 1/6, -1 ≡ a, b, c
Hence, the direction vector of the line is B = (1/3)![]() + (1/6)
+ (1/6)![]() –
– ![]()
Now, the vector form of the equation of the line is given by
r = a + λ b
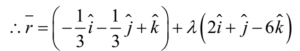
Where λ ∈ R, and is a scalar/parameter
Example 12:
- Find the vector equation of a line whose cartesian equation is 2x – 2 = 3y + 1 = 6z – 2. Find the fixed point through which it passes and its. d.r.s.
- Solution:
The equation of the line is 2x – 2 = 3y + 1 = 6z – 2
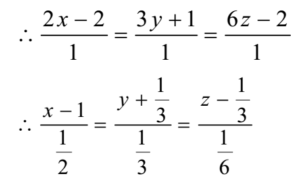
Thus the line passes through the point (1, – 1/3, 1/3)
The position vector of this point is a = ![]() – (1/3)
– (1/3)![]() + (1/3)
+ (1/3)![]()
The d.r. s of the line are i.e. 3, 2, 1≡ a, b, c
Hence, the direction vector of the line is b = 3 ![]() + 2
+ 2![]() +
+ ![]()
Now, the vector form of the equation of the line is given by
r = a + λ b
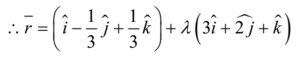
Where λ ∈ R, and is a scalar/parameter
Example 13:
- Find the vector equation of a line whose cartesian equation is 3x – 1 = 6y + 2 = 1 – z
- Solution:
The cartesian equation of the line is 3x – 1 = 6y + 2 = 1 – z
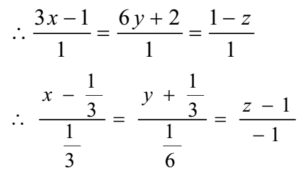
Thus the line passes through the point (1, – 1/3, 1)
The position vector of this point is a = ![]() – (1/3)
– (1/3)![]() +
+ ![]()
The d.r. s of the line are i.e. 1/3, 1/6, – 1 i.e. 2, 1, -6 ≡ a, b, c
Hence, the direction vector of the line is b = 2 ![]() +
+ ![]() – 6
– 6![]()
Now, the vector form of the equation of the line is given by
r = a + λ b
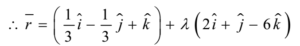
Where λ ∈ R, and is a scalar/parameter