Science > Chemistry > States of Matter > Boyle’s Law
Mathematical relationships between volume, pressure, and temperature of a given mass of gas are referred to as Gas laws. In this article. we shall study Boyle’s Law.
Boyle’s Law:
In 1662, Robert Boyle, on the basis of his experiments put forward the law. It is the relation between the volume and the pressure of enclosed gas at constant temperature.
Statement:
At constant temperature, the volume of a certain mass of enclosed gas varies inversely with its pressure.
Explanation:
Let P be the pressure and V be the volume of a certain mass of enclosed gas, then at the constant temperature
P ∝ 1/V
Thus PV = Constant.
Thus, for a given amount of the gas, the product of pressure and volume is constant at constant temperature.
If V1 and V2 are the volumes of a gas at pressures P1 and P2 respectively at a constant temperature.
P1V1 = P2V2
This relation is called the mathematical statement of Boyle’s Law.
Graphical Representation:
Graph of Pressure (P) Versus Volume (V):
A graph is drawn by taking volume on the x-axis and pressure on the y-axis. The graph is as follows. This graph is also known as PV diagram.
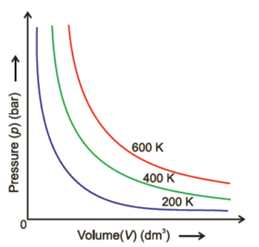
Each curve is rectangular hyperbola and corresponds to a different constant temperature and is known as an isotherm (constant temperature plot). Higher curves correspond to higher temperatures. It should be noted that volume of the gas doubles if pressure is halved.
Graph of Pressure (P) Versus Reciprocal of Volume (1 / V):
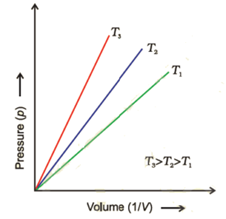
The straight lines obtained in the graph confirms that P ∝ 1/V.
Graph of Product of Pressure and Volume (PV) Versus Pressure (P):
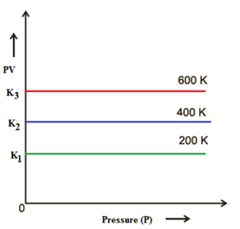
The graph parallel to x-axis confirms that at a particular temperature of the gas, the product of its volume and corresponding pressure is always constant.
Graphs in terms of Logarithmic Variations:
By Boyle’s law, we have PV = k = constant
Taking log of both sides
Log P + Log V = log K
∴ LogP = – LogV + log K
∴ LogP = log (1/V) + log k

Relation Between Density and Pressure:

Thus the density of the certain mass of an enclosed gas is directly proportional to its pressure.
Boyle’s Law and Kinetic Theory of Gases:
According to the kinetic theory of gases, gas consists of a large number of minute particles which are always in constant random motion. During this process, they collide with each other and with the walls of the container containing it. When molecules collide with the walls of the container, there is a change in the momentum of the colliding molecules. This is the cause of the pressure of the gas. According to the kinetic theory of gases, the kinetic energy of molecules is directly proportional to the absolute temperature of the gas. In Boyle’s law temperature is constant. Hence the kinetic energy of the molecules is a constant.
For enclosed gas, the number of molecules of a gas is constant. When the volume of a gas is reduced, the molecules are forced more closer together. Thus the density of gas increased and they collide more frequently. Hence at less volume, there are more collisions and hence more pressure. When the volume of a gas is increased, the molecules are away from each other and they collide less frequently. Hence at larger volumes, there are fewer collisions and hence less pressure. So at a constant temperature, the volume and pressure of a gas are inversely proportional.
Significance of Boyle’s Law:
- Boyle’s law is significant because it explains how gases behaviour at constant temperature and the relation between the pressure and the volume of the gas. According to Boyle’s law, at a constant temperature, the pressure and volume of a gas are inversely proportional to each other.
- At constant temperature, the density of a gas is directly proportional to its pressure.
- Atmospheric pressure is low at high altitudes, so air is less dense. Hence, a lesser quantity of oxygen is available for breathing. This is the reason why mountaineers have to carry oxygen cylinders with them.
Numerical Problems:
Example – 01:
5 dm3 volume of a gas exerts a pressure of 2.02 × 105 kPa. This gas is completely pumped into another tank where it exerts a pressure of 1.01 × 105 kPa at the same temperature, calculate the volume of the tank
Given: Initial volume = V1 = 5 dm3, Initial pressure = P1 = 2.02 × 105 kPa, Final pressure P2 = 1.01 1 kPa, Temperature constant
To Find: Final volume = V2 =?
Solution:
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ V2 = P1V1 /P2
∴ V2 = 2.02 × 105 kPa × 5 dm3 / 1.01 × 105 kPa
∴ V2 = 10 dm3
Hence the volume of the tank is 10 dm3.
Example – 02:
Given the mass of a gas occupies a volume of 2.5 dm3 at NTP. Calculate the change in volume of gas at same temperature if the pressure of the gas is changed to 1.04 × 105 Nm-2.
Given: Initial volume = V1 = 2.5 dm3, Initial pressure = P1 = 1.013 × 105 Nm-2 (Normal pressure), Final pressure P2 = 1.04 × 105 Nm-2, Temperature constant
To Find: Final volume = V2 =?
Solution:
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ V2 = P1V1 /P2
∴ V2 = 1.013 × 105 Nm-2 × 2.5 dm3 / 1.04 × 105 Nm-2
∴ V2 = 2.435 dm3
∴ Change in volume = V1 – V2 = 2.5 dm3 – 2.435 dm3 = 0.065 dm3
Hence the change in volume of the gas is 0.065 dm3.
Example – 03:
A balloon is inflated with helium gas at room temperature of 25 oC and at 1 bar pressure when its initial volume is 2.27 L and allowed to rise in the air. As it rises the external pressure decreases and volume of the gas increases till finally, it bursts when external pressure is 0.3 bar. What is the limit to which volume of the balloon can be inflated?
Given: Initial volume = V1 = 2.27 L, Initial pressure = P1 = 1 bar, Final pressure P2 = 0.3 bar, Temperature constant
To Find: Final volume = V2 =?
Solution:
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ V2 = P1V1 /P2
∴ V2 = 1 bar × 2.27 L/ 0.3 bar
∴ V2 = 7.567 L
Thus balloon can be inflated to the maximum volume of 7.567 L.
Example – 04:
The volume of given mass of a gas is 0.6 dm3 at a pressure of 101.325 kPa. Calculate the volume of the gas if its pressure is ballooned to 142.860 kPa at the same temperature.
Given: Initial volume = V1 = 0.6 dm3, Initial pressure = P1 = 101.325 kPa, Final pressure P2 = 142.860 kPa, Temperature constant
To Find: Final volume = V2 =?
Solution:
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ V2 = P1V1 /P2
∴ V2 = 101.325 kPa × 0.6 dm3 / 142.860 kPa
∴ V2 = 0.426 dm3
Thus final volume of the gas is 0.426 dm3.
Example – 05:
In a J tube partially filled with mercury, the volume of the air column is 4.2 mL and the mercury level in the two limbs is the same. Some mercury is now added to the tube so that the volume of air enclosed in the shorter limb is now 2.8 mL. What is the difference in the level of mercury in this case? Atmospheric pressure is 1 bar.
Given: Initial volume = V1 = 4.2 mL, Initial pressure = P1 = 1 bar, Final volume V2 = 2.8 mL Temperature constant
To Find: Difference in mercury levels =?
Solution:
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ P2 = P1V1 /V2
∴ P2 = 1 bar × 4.2 mL / 2.8 mL
∴ P2 = 1.5 bar
Difference in pressure = P2 – P1 = 1.5 bar – 1 bar = 0.5 bar
Now 1 bar corresponds to 750.12 mm of mercury
Hence 0.5 bar corresponds to 750.12 x 0.5 =375.06 mm of mercury
Hence the difference in mercury levels is 375.06 mm or 37.51 cm
Example – 06:
A thin glass bulb of 100 mL capacity is evacuated and kept in 2.0 L container at 27 °C and 800 mm pressure. If the bulb implodes isothermally, calculate the new pressure in the container in kPa.
Given: Initial Volume = 2000 mL – 100 mL = 1900 mL
To Find: Final pressure =?
Solution:
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ P2 = P1V1 /V2
∴ P2 = 800 mm × 1900 L / 2000 mL
∴ P2 = 76o mm = 760 mm/760 mm = 1 atm = 101.325 kPa
Hence the new pressure is 101.325 kPa
Example – 07:
Certain bulb A containing gas at 1.5 bar pressure was put into communication with an evacuated vessel of 1.0 dm3 capacity through the stop cock. The final pressure of the system dropped to 920 mbar, at the same temperature. What is the volume of container A.
Given: Initial pressure P1 = 1.5 bar, Final Pressure = 920 mbar = 0.920 bar. Let V dm3 be the volume of the container A. Initial Volume = V1 = V dm3, Final Volume = (1.0 + V) dm3
To Find: Volume of container A = V =?
Solution:
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ 1.5 bar × V dm3 = 0.920 bar × (100 – V) dm3
∴ 1.5 V = 92 – 0.920V
∴ 1.5 V + 0.920V = 92
∴ 2.42 V = 92
∴ V = 92 / 2.42 = 39.02
Hence the volume of container A is 38.02 dm³.
Example – 08:
What will be the minimum pressure required to compress 500 dm³ of air at 1 bar to 200 dm³ at 30 °C
Given: Initial volume = V1 = 500 dm³, Initial pressure = P1 = 1 bar, Final volume V2 = 200 dm³ Temperature constant
To Find: Final Pressure = P2 =?
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ P2 = P1V1 /V2
∴ P2 = 1 bar × 500 dm³ / 200 dm³
∴ P2 = 2.5 bar
Hence minimum pressure required = 2.5 bar
Example – 09:
A vessel of 120 mL capacity contains a certain amount of gas at 35 °C and 1.2 bar pressure. The gas is transferred to another vessel of volume 180 mL at 35 °C. What would be the pressure?
Given: Initial volume = V1 = 120 mL, Initial pressure = P1 = 1.2 bar, Final volume V2 = 180 mL, Temperature constant
To Find: Final Pressure = P2 =?
At constant temperature by Boyle’s law
P1V1 = P2V2
∴ P2 = P1V1 /V2
∴ P2 = 1.2 bar × 120 dm³ / 180 dm³
∴ P2 = 0.8 bar
Hence minimum pressure required = 0.8 bar