Science > Mathematics > Coordinate Geometry > Straight Lines > The Inclination of a Line
In this article, we shall study the concept of inclination of a line and the slope of the line
The inclination of a Line:
A line in a coordinate plane forms two angles with the x-axis, which are supplementary. The angle (say) θ made by the line l with the positive direction of the x-axis and measured anti-clockwise is called the inclination of the line. Thus 0° ≤ θ ≤ 180°.
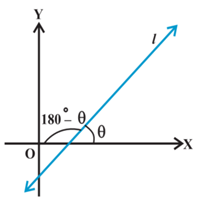
- The lines parallel to the x-axis, or the coinciding with the x-axis, have the inclination of 0°.
- The inclination of a vertical line (parallel to or coinciding with y-axis) is 90°.
The slope of a Line:
If θ is the inclination of a line l, then tan θ, (θ ≠ 90°) is called the slope or gradient of the line l. Note that the slope of a line whose inclination is 90° is not defined. The slope of a line is denoted by the letter, ‘m’. Thus by definition m = tan θ, θ ≠ 90°
- The slope of the x-axis is zero and the slope of the y-axis is not defined
Equation for Slope of a Line:
Let P(x1, y1) and Q(x2, y2) be two points on non-vertical line l whose inclination is θ. As the line is vertical, x1 ≠ x2, The inclination of the line l may be acute or obtuse. Let us consider both of these cases.
Case – 1: When the inclination is acute
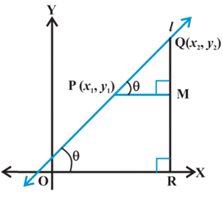
Draw perpendicular QR to the x-axis and PM perpendicular to RQ as shown
MQ = y2 – y1 and MP = x2 – x1∠MPQ = θ ………… (1)
Therefore, the slope of line l = m = tan θ.
But in ∆MPQ, we have
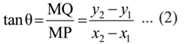
∴ Slope of line l = (y2 – y1)/(x2 – x1)
Case – 2: When the inclination is obtuse

Draw perpendicular QR to the x-axis and PM perpendicular to RQ as shown
MQ = y2 – y1 and MP = x1 – x2∠MPQ = π – θ
Therefore, the slope of line l = m = tan θ = – tan (π – θ).
But in ∆MPQ, we have

∴ Slope of line l = (y2 – y1)/(x2 – x1)
Thus, in either case, the slope of the line is m = (y2 – y1)/(x2 – x1)
Sign of Slope:
The slope can be positive, zero or negative
- Positive slope: This means the angle of inclination θ is such that 0° < θ < 90°. i.e. the angle of inclination is acute.
- Zero slope: This means the line is parallel to the x-axis.
- Negative slope: This means the angle of inclination θ is such that 90° < θ < 180°. i.e. the angle of inclination is obtuse.
- If the line is perpendicular to the x-axis its slope is not defined.
Conditions for parallelism of lines in terms of their slopes
In a coordinate plane, suppose that non-vertical lines l1 and l2 have slopes m1 and m2, respectively. Let their inclinations be α and β, respectively.

If the line l1 is parallel to l2 (Fig 10.4), then their inclinations are equal,
i.e., α = β, and hence, tan α = tan β
Therefore m1 = m2, i.e., their slopes are equal.
Conversely, if the slope of the two lines l1 and l2 are the same, i.e., m1 = m2.
By the property of tangent function (between 0° and 180°), α = β. Therefore, the lines are parallel. Hence, two non-vertical lines l1 and l2 are parallel if and only if their slopes are equal
Conditions for perpendicularity of lines in terms of their slopes:

If the lines l1 and l2 are perpendicular, then by exterior angle property,
β = α + 90°.
∴ tan β = tan (α + 90°)
∴ tan β = – cotα
∴ tan β = – 1/ tan α
∴ tanα . tan β = – 1
∴ m1 . m2 = – 1
Conversely, if m1 m2 = – 1, i.e., tan α tan β = – 1.
Then tanα = – cot β = tan (β + 90°) or tan (β – 90°)
Therefore,α and β differ by 90°.
Thus, lines l1 and l2 are perpendicular to each other.
Hence, two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other, or the product of their slopes is – 1.
Slope of Line from Inclination of a Line:
Tangent Functions of Some Angles:
| Angle | 15° | 30° | 45° | 60° | 75° | 105° | 120° | 135° | 150° |
| tanθ | 2 – 2√3 | 1/√3 | 1 | √3 | 2 + √3 | -(2 + √3) | – √3 | – 1 | – 1/√3 |
Example – 01:
Find the slope of lines whose inclinations are
- 45°
Given θ = 45°
∴ The slope of a line = m = tan θ = tan 45° = 1
- 60°
Given θ = 60°
∴ The slope of a line = m = tan θ = tan 60° = √3
- 30°
Given θ = 30°
∴ The slope of a line = m = tan θ = tan 30° = 1/√3
- 120°
Given θ = 120°
∴ The slope of a line = m = tan θ = tan 120°
∴ m = tan (90° + 30°) = – cot 30° = – √3
- (3π/4)c
Given θ = (3π/4)c
∴ The slope of a line = m = tan θ = tan (3π/4)c
∴ m = tan (π/2 + π/4)c = – tan (π/4)c = – 1/√2
- (5π/6)c
Given θ = (5π/6)c
∴ The slope of a line = m = tan θ = tan (5π/6)c
∴ m = tan (π – π/6)c = – tan (π/6)c = – 1/√3
- 105°
Given θ = 105°
∴ The slope of a line = m = tan θ
= tan 105° = tan (60° + 45°)

- The line makes an angle of 30° with the positive direction of the y-axis measured anticlockwise.
The angle made by line with the positive direction of the y-axis = – 30° (anticlockwise)
The angle made by line with positive direction of the x-axis = 90° – 30° = 60°
Now θ = 60°
∴ The slope of a line = m = tan θ = tan 60° = √3
Example – 02:
Find the inclinations of lines whose slopes are
- 1
The slope of line = m = tan θ =1
∴ θ = tan-1(1) = 45° or (π/4)c
- – 1
The slope of line = m = tan θ = -1
∴ θ = tan-1(-1) = 135° or (3π/4)c
- √3
The slope of line = m = tan θ =√3
∴ θ = tan-1(√3) = 60° or (π/3)c
- – √3
The slope of line = m = tan θ = -√3
∴ θ = tan-1(- √3) = 120° or (2π/3)c
- 1/√3
The slope of line = m = tan θ =1/√3
∴ θ = tan-1(1/√3) = 30° or (π/6)c
- – 1/√3
The slope of line = m = tan θ = – 1/√3
∴ θ = tan-1(- 1/√3) = 150° or (5π/6)c
One reply on “The Inclination of a Line”
excellent for understanding