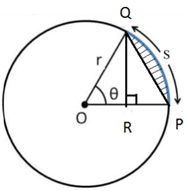
Science > Mathematics > Trigonometry > Angle Measurement > Area of Sector
In this article, we shall study to solve problems based on the area of the sector.
Example – 01:
Find the area of a sector of the circle which subtends an angle of 120° at the centre, if the radius of the circle is 6 cm.
Given: Angle subtended at centre = θ = 120° = 120 x (π/180) = (2π/3)c , Radius of circle = r = 6 cm.
To find: Area of sector = A =?
Solution:
Area of sector = ½ r2θ= ½ x 62 x (2π/3) =12π sq. cm
Ans: The area of the sector is 12π sq. cm
Example – 02:
The area of the circle is 81π sq. cm. Find the length of its arc subtending an angle of 150° at the centre. Also, find the area of the corresponding sector.
Given: Area of circle = 81π sq. cm, Angle subtended at centre = θ = 150° = 150 x (π/180) = (5π/6)c ,
To find: Length of arc = S = ?, Area of sector = A = ?
Solution:
Area of circle = πr2 = 81π
∴ r2 = 81
∴ r = 9 cm
Length of arc = S = r θ = 9 x (5π/6) = 7.5 π cm
Area of sector = ½ r2θ= ½ x 92 x (5π/6) = 33.75 π sq. cm
Ans: length of the arc is 7.5 π cm and the area of the sector is 33.75 π sq. cm
Example – 03:
The area of a circle is 25π sq. cm. Find the length of its arc subtending an angle of 144° at the centre. Also, find the area of the corresponding sector.
Given: Area of circle = 25π sq. cm, Angle subtended at centre = θ = 144° = 144 x (π/180) = (4π/5)c ,
To find: Length of arc = S = ?, Area of sector = A = ?
Area of circle = πr2 = 25π
∴ r2 = 25
∴ r = 5 cm
Length of arc = S = r θ = 5 x (4π/5) = 4π cm
Area of sector = ½ r2θ= ½ x 52 x (4π/5) = 10π sq. cm
Ans: length of the arc is 4π cm and the area of the sector is 10π sq. cm
Example – 04:
The area of a circle is 81π sq. cm. Find the length of its arc subtending an angle of 300° at the centre. Also, find the area of the corresponding sector.
Given: Area of circle = 81π sq. cm, Angle subtended at centre = θ = 300° = 300 x (π/180) = (5π/3)c ,
To find: Length of arc = S = ?, Area of sector = A = ?
Area of circle = πr2 = 81π
∴ r2 = 81
∴ r = 9 cm
Length of arc = S = r θ = 9 x (5π/3) = 15π cm
Area of sector = ½ r2θ= ½ x 92 x (5π/3) = 67.5 π sq. cm
Ans: length of the arc is 15π cm and the area of the sector is 67.5π sq. cm
Example – 05:
The perimeter of a sector of a circle of area 25π sq. cm is 20 cm. Find the area of the sector.
Given: Area of circle = 25π sq. cm, Perimeter = 20 cm
To find: Area of sector = A = ?
Area of circle = πr2 = 25π
∴ r2 = 25
∴ r = 5 cm
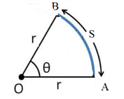
Perimeter of sector = r + r + s = 20
∴ 2r + r θ = 20
∴ r (2 + θ) = 20
∴ 5 (2 + θ) = 20
∴ 2 + θ = 4
∴ θ = 2c
Area of sector = ½ r2θ= ½ x 52 x 2 = 25 sq. cm
Ans: The area of the sector is 25 sq. cm
Example – 06:
The perimeter of a sector of a circle of area 64π sq. cm is 56 cm. Find the area of the sector.
Given: Area of circle = 64π sq. cm, Perimeter = 56 cm
To find: Area of sector = A = ?
Area of circle = πr2 = 64π
∴ r2 = 64
∴ r = 8 cm
Perimeter of sector = r + r + s = 56
∴ 2r + r θ = 56
∴ r (2 + θ) = 56
∴ 8 (2 + θ) = 56
∴ 2 + θ = 7
∴ θ = 5c
Area of sector = ½ r2θ= ½ x 82 x 5 = 160 sq. cm
Ans: The area of the sector is 160 sq. cm
Example – 07:
Find the area of sector whose arc length is 30π cm and the angle of the sector is 40°.
Given: Length of arc = 30π cm, angle of sector = θ = 40° = 40 x π/180 = (2π/9)c ,
To find: Area of sector = A = ?
Length of arc = S = r θ
∴ 30π = r x (2π/9)
∴ r = 135 cm
Area of sector = ½ r2θ= ½ x 1352 x (2π/9) = 2025π sq. cm
Ans: The area of the sector is 2025 sq. cm
Example – 08:
In a circle of radius 12 cm, an arc PQ subtends the angle of 30° at the centre. Find the area between arc PQ and chord PQ.
Given: radius of circle = r = 12 cm, angle subtended at the centre = θ = 30° = 30 x (π/180) = (π/6)c ,
To find: the area between arc PQ and chord PQ.
Solution:

Area of sector = ½ r2θ= ½ x 122 x (π/6) = 12π sq. cm
In Δ OOR, sin 30° = QR/OQ
∴ OR = OQ sin 30° = 12 x 1/2 = 6 cm
Area of Δ POQ = ½ x base x height = ½ x OP x QR = ½ x 12 x 6 = 36 sq.cm.
Area of shaded region = Area of sector – Area of Δ POQ
∴ Area of shaded region = 12π – 36 = 12(π – 3) sq. cm
Ans: The area between arc PQ and chord PQ is 12(π – 3) sq. cm
Example – 09:
OPQ is the sector of a circle with centre O and radius 12 cm. if m ∠ POQ= 60°, find the difference between the areas of sector POQ and Δ POQ.
Given: radius of circle = r = 12 cm, angle subtended at the centre = θ = 60° = 60 x (π/180) = (π/3)c ,
To find: the difference between the areas of sector POQ and Δ POQ.
Solution:

Area of sector = ½ r2θ= ½ x 122 x (π/3) = 24π sq. cm
In Δ OQR, sin 60° = QR/OQ
∴ OR = OQ sin 60° = 12 x √3 /2 = 6√3 cm
Area of Δ POQ = ½ x base x height = ½ x OP x QR = ½ x 12 x 6√3 = 36√3 sq.cm.
Area of shaded region = Area of sector – Area of Δ POQ
∴ Area of shaded region = 24π – 36√3 = 12(2π – 3√3) sq. cm
Ans: The difference between the areas of sector POQ and Δ POQ. is 12(2π – 3√3) sq. cm
Example – 10:
OPQ is a sector of a circle with centre O and radius 12 cm. if m∠OPQ = 30°, Find the area between arc PQ and chord PQ.
Given: radius of circle = r = 12 cm,
To find: the area between arc PQ and chord PQ.
Solution:

Δ OPQ is isosceles triangle
m∠ OPQ = m∠ OQP = 30°
m∠ POQ = θ = 120° = 120 x π/180 = (2π/3)c
Area of sector = ½ r2θ= ½ x 122 x (2π/3) = 48π sq. cm
Δ OQR is 30°-60°-90° triangle
OR = ½OQ = ½ x 12 = 6 cm
QR = √3 /2 OQ = √3 /2 x 12 = 6√3
PQ = 2 QR = 2 x 6√3 = 12√3
Area of Δ POQ = ½ x base x height = ½ x PQ x OR = ½ x 12√3 x 6 = 36√3 sq.cm.
Area of shaded region = Area of sector – Area of Δ POQ
∴ Area of shaded region = 48π – 36√3 = 12(4π – 3√3) sq. cm
Ans: The area between arc PQ and chord PQ. is 12(4π – 3√3) sq. cm
Example – 11:
Two circles each of radius 7 cm intersect each other such that the distance between their centres is 7√2 cm. Find area common to both the circles.
Given: radius of circle = r = 7 cm, Distance between centres = 7√2 cm
To find: the area of common portion = ?
Solution:

In quadrilateral ADBC
AD = DB = BC = CA = 7cm
diagonal AB = 7√2 cm
Hence quadrilateral ADBC is a square with each angle 90°
This is central angle subtended for sectors of both the circles = θ = 90° = 90 x π/180 = (π/2)c
Area of common region = area of sector (A-CED) + Area of sector (B-CFD) – area of square ADBC
∴ Area of common region = ½ r2θ + ½ r2θ – r2
∴ Area of common region = r2 θ – r2
∴ Area of common region = r2 ( θ – 1)
∴ Area of common region = 72 ( π/2 – 1)
∴ Area of common region = 49(π/2 – 1) sq. cm
Ans: The area common to both the circle is 49(π/2 – 1) sq. cm