Science > Mathematics > Pair of Straight Lines > To Find Value of Constant When Relation Between Slopes is Given
In this article, we shall study to solve problems to find the value of constant or to prove the given relation when the relation between slopes of the line represented by the joint equation is given.
Remember:
- If m1 and m2 are the slopes of the two lines represented by joint equation ax2 + 2hxy + by2 = 0. Then m1. m2 = a/b ; m1 + m2 = -2h/b and remember (m1 – m2) 2 = (m1+ m2)2 – 4m1.m2.
Algorithm:
- Write given of joint equation.
- Compare with the standard equation.
- Find values of a, h and b.
- Use above relations between slopes
- Solve equations and get the value of constant
Example – 01:
- Show that the equation 3x2 – 4xy + y2 = 0 represents the pair of lines whose slopes differ by 2.
- Solution:
The given joint equation is 3x2 – 4xy + y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 3, 2h = – 4, and b = 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = -(-4)/1 = 4 and m1 . m2 = a/b = 3/1 = 3
Using (m1 – m2)2 = (m1 + m2)2 – 4 m1 . m2
∴ (m1 – m2)2 = (4)2 – 4 (3)
∴ (m1 – m2)2 = 16 – 12
∴ (m1 – m2)2 = 4
Taking square roots of both sides we get,
| m1 – m2| = 2
Hence the slopes differ by 2.
Example – 02:
- Show that the equation 77x2 – 36xy + 4y2 = 0 represents the pair of lines whose slopes differ by 2.
- Solution:
The given joint equation is 77x2 – 36xy + 4y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 77, 2h = – 36, and b = 4
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = -(-36)/4 = 9 and m1 . m2 = a/b = 77/4
Using (m1 – m2)2 = (m1 + m2)2 – 4 m1 . m2
∴ (m1 – m2)2 = (9)2 – 4 (77/4)
∴ (m1 – m2)2 = 81 – 77
∴ (m1 – m2)2 = 4
Taking square roots of both sides we get,
| m1 – m2| = 2
Hence the slopes differ by 2.
Example – 03:
- Show that the difference of the slopes of the two lines represented by equation x2(tan2θ + cos2θ) – 2xy tanθ + y2sin2θ = 0 is 2.
- Solution:
The given joint equation is x2(tan2θ + cos2θ) – 2xy tanθ + y2sin2θ = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = (tan2θ + cos2θ), 2h = – 2tanθ, and b = sin2θ
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = -(- 2tanθ)/sin2θ = 2tanθ)/sin2θ
and m1 . m2 = (tan2θ + cos2θ)/sin2θ
Using (m1 – m2)2 = (m1 + m2)2 – 4 m1 . m2
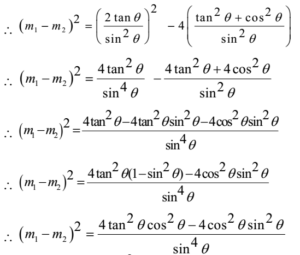
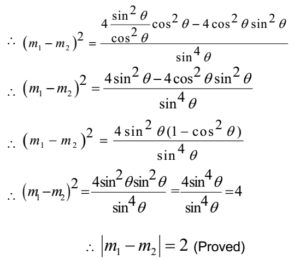
Hence the slopes differ by 2.
Example – 04:
- Show that the difference of the slopes of the two lines represented by equation (tan2θ + 3)(tan2θ – 1)x2 – 2xy sec2θ + y2 = 0 is 4.
- Solution:
The given joint equation is (tan2θ + 3)(tan2θ – 1)x2 – 2xy sec2θ + y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = (tan2θ + 3)(tan2θ – 1), 2h = – 2sec2θ, and b = 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = -(- 2sec2θ)/1 = 2sec2θ
and m1 . m2 = (tan2θ + 3)(tan2θ – 1)/1 = (tan2θ + 3)(tan2θ – 1)
Using (m1 – m2)2 = (m1 + m2)2 – 4 m1 . m2
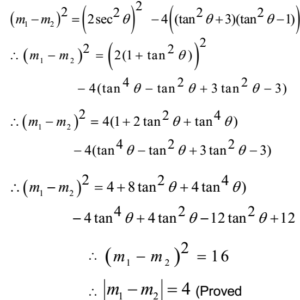
Hence the slopes differ by 4.
Example – 05:
- Find λ, if the difference of the slopes of the lines λx2 + 6xy – 4y2 = 0 is equal to their product.
- Solution:
The given joint equation is λx2 + 6xy – 4y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = λ, 2h = 6, and b = – 4
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = -6/-4 = 3/2 and m1 . m2 = a/b = λ/-4 = – λ/4
Given the relation between slopes
| m1 – m2| = m1 . m2
squaring both sides
(m1 – m2)2 = (m1 . m2)2
∴ (m1 + m2)2 – 4 m1 . m2= (m1 . m2)2
∴ (3/2)2 – 4 (- λ/4)= (- λ/4)2
∴ 9/4 + λ = λ2/16
Multiplying both sides of equation by 16
∴ 36 + 16λ = λ2
∴ λ2 – 16λ – 36 = 0
∴ (λ – 18)(λ + 2) = 0
∴ λ = 18 or λ = – 2
Example – 06:
- Find k, if the difference of the slopes of the lines 3x2 + kxy – y2 = 0 is 4.
- Solution:
The given joint equation is 3x2 + kxy – y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 3, 2h = k, and b = – 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = -k/-1 = k and m1 . m2 = a/b = 3/-1 = – 3
Given the relation between slopes
| m1 – m2| = 4
squaring both sides
(m1 – m2)2 = 16
∴ (m1 + m2)2 – 4 m1 . m2= 16
∴ (k)2 – 4 (- 3)= 16
∴ k2 + 12 = 16
∴ k2 = 4
∴ k = ± 2
Example – 07:
- Find k if the slopes of lines given by kx2 + 5xy + y2 = 0 differ by 1.
- Solution:
The given joint equation is kx2 + 5xy + y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = k, 2h = 5, and b = 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – 5/1 = – 5 and m1 . m2 = a/b = k/1 = k
Given the relation between slopes
| m1 – m2| = 1
squaring both sides
(m1 – m2)2 = 1
∴ (m1 + m2)2 – 4 m1 . m2= 1
∴ (-5)2 – 4 k= 1
∴ 25 – 4 k= 1
∴ – 4 k= – 24
∴ k = 6
Example – 08:
- Find k, if the slope of one of the lines given by kx2 + 4xy – y2 = 0 exceeds the slope of other by 8.
- Solution:
The given joint equation is kx2 + 4xy – y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = k, 2h = 4, and b = – 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – 4/-1 = 4 and m1 . m2 = a/b = k/-1 = – k
Given the relation between slopes
| m1 – m2| = 8
squaring both sides
(m1 – m2)2 = 64
∴ (m1 + m2)2 – 4 m1 . m2= 64
∴ (4)2 – 4(- k)= 64
∴ 16 + 4 k= 64
∴ – 4 k= 48
∴ k = 12
Example – 09:
- Find k, if the difference between the slopes of the lines 12x2 + k xy – y2 = 0 is 7.
- Solution:
The given joint equation is 12x2 + k xy – y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 12, 2h = k, and b = – 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – k/-1 = k and m1 . m2 = a/b = 12/-1 = – 12
Given the relation between slopes
| m1 – m2| = 7
squaring both sides
(m1 – m2)2 = 49
∴ (m1 + m2)2 – 4 m1 . m2= 49
∴ (k)2 – 4(- 12)= 49
∴ k2 + 48 = 49
∴ k2 = 1
∴ k = ± 1
Example – 10:
- Find k, if the slope of one of the lines given by 3x2 + 4xy + ky2 = 0 is three times the slope of the other.
- Solution:
The given joint equation is 3x2 + 4xy + ky2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 3, 2h = 4, and b = k
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – 4/k and m1 . m2 = a/b = 3/k
Given the relation between slopes
m1 = 3m2


∴ k2 = k
∴ k2 – k = 0
∴ k (k – 1) = 0
∴ k = 0 and k = 1
But k cannot be zero.
∴ k = 1
Example – 11:
- Find k, if the slope of one of the lines given by kx2 + 4xy – y2 = 0 is three times the slope of the other.
- Solution:
The given joint equation is kx2 + 4xy – y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = k, 2h = 4, and b = – 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – 4/-1 = 4, and m1 . m2 = a/b = k/-1 = – k
Given the relation between slopes
m1 = 3m2
Now, m1 + m2 = 4
∴ 3m2 + m2 = 4
∴ 4m2 = 4
∴ m2 = 1
∴ m1 = 3m2 = 3 x 1 = 3
Now, m1 . m2 = – k
∴ (3)(1) = – k
∴ k = – 3
Example – 12:
- Find k, if the slope of one of the lines given by 4x2 + kxy + y2 = 0 is four times the slope of the other.
- Solution:
The given joint equation is 4x2 + kxy + y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 4, 2h = k, and b = 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – k/1 = – k, and m1 . m2 = a/b = 4/1 = 4
Given the relation between slopes
m1 = 4m2
Now, m1 + m2 = – k
∴ 4m2 + m2 = – k
∴ 5m2 = – k
∴ m2 = – k/5
Now, m1 . m2 = 4
∴ 4m2 . m2 = 4
∴ (m2)2 = 1
∴ (- k/5)2 = 1
∴ (- k/5) = ± 1
∴ k = ± 5
Example – 13:
- Find k, if the slope of one of the lines given by 5x2 + kxy + y2 = 0 is five times the slope of the other.
- Solution:
The given joint equation is 5x2 + kxy + y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 5, 2h = k, and b = 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – k/1 = – k, and m1 . m2 = a/b = 5/1 = 5
Given the relation between slopes
m1 = 5m2
Now, m1 + m2 = – k
∴ 5m2 + m2 = – k
∴ 6m2 = – k
∴ m2 = – k/6
Now, m1 . m2 = 5
∴ 5m2 . m2 = 5
∴ (m2)2 = 1
∴ (- k/6)2 = 1
∴ (- k/6) = ± 1
∴ k = ± 6
Example – 14:
- Find k if the sum of the slopes of lines given by kx2 + 8xy + 5 y2 = 0 is twice the product of the slopes.
- Solution:
The given joint equation is kx2 + 8xy + 5 y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = k, 2h = 8, and b = 5
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – 8/5, and m1 . m2 = a/b = k/5
Given the relation between slopes
m1 + m2 = 2 m1 . m2
-8/5 = 2 x k/5
∴ k = – 4
Example – 15:
- Find k if the sum of the slopes of lines given by 2x2 + kxy -3y2 = 0 is equal to the product of the slopes.
- Solution:
The given joint equation is 2x2 + kxy -3y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 2, 2h = k, and b = -3
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – k/-3 = k/3, and m1 . m2 = a/b = 2/-3 = – 2/3
Given the relation between slopes
m1 + m2 = m1 . m2
k/3 = (-2/3)
∴ k = – 2
Example – 16:
- Find k, if the sum of the slopes of lines given by 3x2 + kxy + y2 = 0 is zero.
- Solution:
The given joint equation is 2x2 + kxy -3y2 = 0
Comparing with ax2 + 2hxy + by2 = 0
Here a = 3, 2h = k, and b = 1
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b = – k/1 = – k, and m1 . m2 = a/b = 3/1 = 3
Given the relation between slopes
m1 + m2 = 0
∴ – k = 0
∴ k = 0
Example – 17:
- Find k, if the slope of one of the lines given by 3x2 – 4xy + ky2 = 0 is 1.
- Solution:
Given joint equation of lines is 3x2 – 4xy + ky2 = 0
It is in the form ax2 + 2hxy + by2 = 0.
a = 3, 2h = – 4 and b= k
The auxiliary equation of given line is of the form
bm2 + 2hm + a = 0
∴ km2 – 4m + 3 = 0 ……… (1)
Slope of one of the line is 1
Substituting m = 1 in equation (1) we get
k(1)2 – 4(1) + 3 = 0
∴ k – 1 = 0
∴ k = 1