In this article, we shall study to find the distance between two points using the distance formula when the coordinates of the two points are given.
Example 01:
- Find the distance between the following pairs of points :
- (2, 3), (4, 1)
Let A(2, 3) ≡ (x1, y1) and B(4, 1) ≡ (x2, y2) be the points
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ AB2 = (4 – 2)2 + (1 – 3)2 = (2)2 + (-2)2 = 4 + 4 = 8
∴ AB =√8 = 2√2 unit
Ans: The distance between given points is 2√2 unit
- (– 5, 7), (– 1, 3)
Let A(-5, 7) ≡ (x1, y1) and B(-1, 3) ≡ (x2, y2) be the points
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ AB2 = (-1 + 5)2 + (3 – 7)2 = (4)2 + (-4)2 = 16 + 16 = 32
∴ AB =√32 = 4√2 unit
Ans: The distance between given points is 4√2 unit
- (6, 8), (– 9, – 12)
Let A(6, 8) ≡ (x1, y1) and B(-9, -12) ≡ (x2, y2) be the points
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ AB2 = (- 9 – 6)2 + (-12 – 8)2 = (-15)2 + (-20)2 = 225 + 400 = 625
∴ AB =√625 = 25 unit
Ans: The distance between given points is 25 unit
- (-6, -1), (– 6, 11)
Let A(-6, -1) ≡ (x1, y1) and B(-6, 11) ≡ (x2, y2) be the points
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ AB2 = (- 6 + 6)2 + (11 + 1)2 = (0)2 + (12)2 = 0 + 144 = 144
∴ AB =√144 = 12 unit
Ans: The distance between given points is 12 unit
- (a, b), (– a, – b)
Let A(a, b) ≡ (x1, y1) and B(-a, -b) ≡ (x2, y2) be the points
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ AB2 = (- a – a)2 + (-b – b)2 = (- 2a)2 + (- 2b)2 = 4a2 + 4b2 = 4(a2 + 4b2)
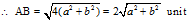
- (0, 0), (36, 15)
Let A(0, 0) ≡ (x1, y1) and B(36, 15) ≡ (x2, y2) be the points
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ AB2 = (36 – 0)2 + (15 – 0)2 = (36)2 + (15)2 = 1296 + 225 = 1521
∴ AB =√1521 = 39 unit
Alternate Direct Method
One of the given point is origin O. Let A(36, 15) ≡ (x, y)
∴ OA2 = x2 + y2 = (36)2 + (15)2 = 1296 + 225 = 1521
∴ OA =√1521 = 39 unit
Ans: The distance between given points is 39 unit
Example 02:
- Using distance formula show that following sets of points are collinear
- A(0,4), B(2,10) and C(3,13)
Given points are A(0,4), B(2,10) and C(3,13)
Using distance formula
AB2 = (2 – 0)2 + (10 – 4)2 = (2)2 + (6)2 = 4 + 36 = 40
∴ AB = √40 = 2√10 unit …………….. (1)
BC2 = (3 – 2)2 + (13 – 10)2 = (1)2 + (3)2 = 1 + 9 = 10
∴ BC = √10 unit …………….. (2)
AC2 = (3 – 0)2 + (13 – 4)2 = (3)2 + (9)2 = 9 + 81 = 90
∴ AC = √90 = 3√10 unit …………….. (3)
From equations (1), (2) and (3) we have
AC = AB + BC
∴ A – B – C
Hence points A, B and C are collinear
- P(5, 0), Q(10, -3) and R(-5, 6)
Given points are P(5, 0), Q(10, -3) and R(-5, 6)
Using distance formula
PQ2 = (10 – 5)2 + (-3 – 0)2 = (5)2 + (-3)2 = 25 + 9 = 34
∴ PQ = √34 unit …………….. (1)
QR2 = (-5 – 10)2 + (6 + 3)2 = (-15)2 + (9)2 = 225 + 81 = 306
∴ QR = √306 = 3√34 unit …………….. (2)
PR2 = (-5 – 5)2 + (6 – 0)2 = (-10)2 + (6)2 = 100+ 36 = 136
∴ PR = √136 = 2√34 unit …………….. (3)
From equations (1), (2) and (3) we have
QR = PQ + PR
∴ Q – P – R
Hence points P, Q and R are collinear
- L(2, 5), M(5, 7) and N(8, 9)
Given points are L(2, 5), M(5, 7) and N(8, 9)
Using distance formula
LM2 = (5 – 2)2 + (7 – 5)2 = (3)2 + (2)2 = 9 + 4 = 13
∴ LM = √13 unit …………….. (1)
MN2 = (8 – 5)2 + (9 – 7)2 = (3)2 + (2)2 = 9 + 4 = 13
∴ MN = √13 unit …………….. (2)
LN2 = (8 – 2)2 + (9 – 5)2 = (6)2 + (4)2 = 36+ 16 = 52
∴ LN = √52 = 2√13 unit …………….. (3)
From equations (1), (2) and (3) we have
LN = LM + MN
∴ L – M – N
Hence points L, M and N are collinear
- D(5, 1), E(1, -1) and F(11, 4)
Given points are D(5, 1), E(1, -1) and F(11, 4)
Using distance formula
DE2 = (1 – 5)2 + (-1 – 1)2 = (-4)2 + (-2)2 = 16 + 4 = 20
∴ DE = √20 = 2√5 unit …………….. (1)
EF2 = (11 – 1)2 + (4 + 1)2 = (10)2 + (5)2 = 100 + 25 = 125
∴ EF = √125 = 5√5 unit …………….. (2)
DF2 = (11 – 5)2 + (4 – 1)2 = (6)2 + (3)2 = 36+ 9 = 45
∴ DF = √45 = 3√5 unit …………….. (3)
From equations (1), (2) and (3) we have
EF = DE + DF
∴ E – D – F
Hence points D, E and F are collinear
- A(1, 5), B(2, 3) and C(– 2, – 11)
Given points are A(1, 5), B(2, 3) and C(-2, -11)
Using distance formula
AB2 = (2 – 1)2 + (3 – 5)2 = (1)2 + (-2)2 = 1 + 4 = 5
∴ AB = √5 unit …………….. (1)
BC2 = (-2 – 2)2 + (-11 – 3)2 = (-4)2 + (-14)2 = 16 + 196 = 212
∴ BC = √212 unit …………….. (2)
AC2 = (-2 – 1)2 + (-11 – 5)2 = (-3)2 + (-16)2 = 9 + 256 = 265
∴ AC = √265 unit …………….. (3)
From equations (1), (2) and (3) we have
AC ≠ AB + BC
Hence points A, B and C are not collinear
Example 03:
- Ashima, Bharti, and Camella are seated at A(3, 1), B(6, 4), and C(8, 6) respectively. Do you think they are seated in a line?
Given points are A(3, 1), B(6, 4) and C(8, 6)
Using distance formula
AB2 = (6 – 3)2 + (4 – 1)2 = (3)2 + (3)2 = 9 + 9 = 18
∴ AB = √18 = 3√2 unit …………….. (1)
BC2 = (8 – 6)2 + (6 – 4)2 = (2)2 + (2)2 = 4 + 4 = 8
∴ BC = √8 = 2√2 unit …………….. (2)
AC2 = (8 – 3)2 + (6 – 1)2 = (5)2 + (5)2 = 25 + 25 = 50
∴ AC = √50 = 5√2 unit …………….. (3)
From equations (1), (2) and (3) we have
AC = AB + BC
∴ A – B – C
Hence points A, B and C are collinear.
Thus Ashima, Bharti and Camella are seated in a line
Example 04:
- The distance between the points (0, 0) and (x, 3) is 5. Find x.
Let A(0, 0) ≡ (x1, y1) and B(x, 3) ≡ (x2, y2) be the points.
Thus AB = 5
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ 52 = (x – 0)2 + (3 – 0)2 = x2 + 9
∴ 25 = x2 + 9
∴ x2 = 16
∴ x = ± 4
Example 05:
- The distance between the points (a, 5) and (0, -3) is 4√5 unit. Find a.
Let A(a, 5) ≡ (x1, y1) and B(0, -3) ≡ (x2, y2) be the points.
Thus AB = 4√5
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ (4√5)2 = (0 – a)2 + (-3 – 5)2 = (-a)2 + (-8)2 = a2 + 64
∴ 80 = a2 + 64
∴ a2 = 16
∴ a = ± 4
Example 06:
- The distance between the points (8, -7) and (-4, a) is 13. Find a.
Let A(8, -7) ≡ (x1, y1) and B(-4, a) ≡ (x2, y2) be the points.
Thus AB = 5
By distance formula
AB2 = (x2 – x1)2 + (y2 – y1)2
∴ 132 = (- 4 – 8)2 + (a + 7)2 = (-12)2 + a2 + 14a + 49
∴ 169 = 144 + a2 + 14a + 49
∴ a2 + 14a + 197 – 169 = 0
∴ a2 + 14a + 24 = 0
∴ (a + 12)(a + 2) = 0
∴ a + 12 = 0 or a + 2 = 0
∴ a = -12 and a = -2
Example 07:
- Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.
Given P(2, -3) ≡ (x1, y1) and Q(10, y) ≡ (x2, y2) be the points.
Thus PQ = 10 units
By distance formula
PQ2 = (x2 – x1)2 + (y2 – y1)2
∴ 102 = (10 – 2)2 + (y + 3)2 = (8)2 + y2 + 6y + 9
∴ 100 = 64 + y2 + 6y + 9
∴ 36 = y2 + 6y + 9
∴ y2 + 6y + 9 – 36 = 0
∴ y2 + 6y + – 27 = 0
∴ (y + 9)(y – 3) = 0
∴ y + 9 = 0 or y – 3 = 0
∴ y = -9 and y = 3
Example 08:
- Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).
Let P(2, –5) and Q(–2, 9) be the given points.
Let the point on the x-axis be A(a, 0)
Given PA = QA
PA2 = QA2
Using distance formula
(a – 2)2 + (0 + 5)2 = (a + 2)2 + (0 – 9)2
∴ a2 – 4a + 4 + 25 = a2 + 4a + 4 + 81
∴ – 4a + 25 = + 4a + 81
∴ – 8a = 56
∴ a = – 7
Hence the required point is (-7, 0)
Example 09:
- Find a point on the y-axis which is equidistant from points A(6, 5) and B(– 4, 3).
A(6, 5) and B(– 4, 3) are given points.
Let the point on the y-axis be P(0, b)
Given PA = PB
PA2 = PB2
Using distance formula
(0 – 6)2 + (b – 5)2 = (0 + 4)2 + (b – 3)2
∴ 36 + b2 – 10 b + 25 = 16 + b2 – 6b + 9
∴ 36 – 10 b + 25 = 16 – 6b + 9
∴ – 4b = 25 – 61 = -36
∴ b = 9
Hence the required point is (0, 9)
Example 10:
- Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4)
Let P(3, 6) and Q(–3, 4) be the given points.
Given point A(x, y)
Given PA = QA
PA2 = QA2
Using distance formula
(x – 3)2 + (y – 6)2 = (x + 3)2 + (y – 4)2
∴ x2 – 6x + 9 + y2 – 12y + 36 = x2 + 6x + 9 + y2 – 8y + 16
∴ x2 – 6x + 9 + y2 – 12y + 36 – x2 – 6x – 9 – y2 + 8y – 16 = 0
∴ – 12x – 4y + 20 = 0
∴ 3x + y – 5 = 0
Hence the requiredrelation is 3x + y – 5 = 0
Example 11:
- Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Let P(7, 1) and Q(3, 5) be the given points.
Given point A(x, y)
Given PA = QA
PA2 = QA2
Using distance formula
(x – 7)2 + (y – 1)2 = (x – 3)2 + (y – 5)2
∴ x2 – 14x + 49 + y2 – 2y + 1 = x2 – 6x + 9 + y2 – 10y + 25
∴ x2 – 14x + 49 + y2 – 2y + 1 – x2 + 6x – 9 – y2 + 10y – 25 = 0
∴ – 8x + 8y + 16 = 0
∴ x – y + 2 = 0
Hence the requiredrelation is x – y + 2 = 0
Example 12:
- If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also, find the distances QR and PR.
Given P(5, -3) and R(x, 6) be the given points.
Given point Q(0, 1)
Given PQ = RQ
PQ2 = RQ2
Using distance formula
(5 – 0)2 + (-3 – 1)2 = (x – 0)2 + (6 – 1)2
∴ (5)2 + (-4)2 = (x)2 + (5)2
∴ 25 + 16 = x2 + 25
∴ x2 = 16
∴ x = ± 4
When R(4, -3)
QR2 = (4 – 0)2 + (-3 – 1)2 = (4)2 + (-4)2 = 16 + 16 = 32
∴ QR = √32 = 4√2 unit …………….. (1)
PR2 = (4 – 5)2 + (-3 + 3)2 = (-1)2 + (0)2 = 1 + 0 = 1
∴ PR = √1 = 1 unit …………….. (1)
When R(-4, -3)
QR2 = (-4 – 0)2 + (-3 – 1)2 = (-4)2 + (-4)2 = 16 + 16 = 32
∴ QR = √32 = 4√2 unit …………….. (1)
PR2 = (-4 – 5)2 + (-3 + 3)2 = (-9)2 + (0)2 = 81 + 0 = 81
∴ PR = √81 = 9 unit …………….. (1)
Example 13:
- If P (6, -1), Q(1, 3), and R(x, 8) are the points and PQ = QR, find the values of x.
Given P(6, -1) and R(x, 8) be the given points.
Given point Q(1, 3)
Given PQ = RQ
PQ2 = RQ2
Using distance formula
(1 – 6)2 + (3 + 1)2 = (1 – x)2 + (3 – 8)2
∴ (-5)2 + (-4)2 = x2 – 2x + 1 + (-5)2
∴ 25 + 16 = x2 – 2x + 1 +25
∴ x2 – 2x + 1 – 16 = 0
∴ x2 – 2x + – 15 = 0
∴ (x + 3)(x – 5) = 0
∴ x + 3 = 0 and x – 5 = 0
∴ x = – 3 and x = 5