Science > Physics > Stationary Waves > Numerical Problems Vibration of String Set-03
In this article, we shall study to solve problems to calculate fundamental frequency of vibration of string and its higher frequencies.
Example 01:
A stretched wire of length one metre gives 3 beats per second with a tuning fork. If the length is made 0.99 m, no beats are heard between the two. What is the frequency of fork?
Given: Initial length = l1 = 1m, Final length l2 = 0.99 m, in case 1 |n1 – N| = 3 beats per second, in case 2, n2 = N
To Find: Frequency of Tuning fork = N =?
Solution:
By law length n α 1/l
l1 > l2, hence n1 < n2
n2 – n1 = 3
n1 = n2 – 3
By law of length
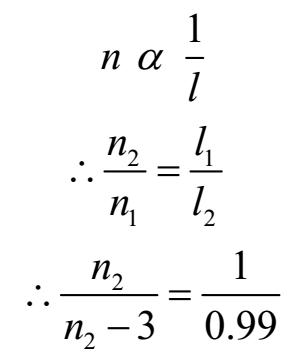
0.99 n2 = n2 – 3
3 = 0.01 n2
n2 = 3/0.01 = 300 Hz
Ans: Frequency of tuning fork is 300 Hz.
Example 02:
A sonometer wire one metre long is stretched by a certain tension and is divided into two segments by a movable knife edge so that the two segments of the vibrating wire differ in length by 2 mm. when set into vibration, the two segments produce 2 beats per second. Find their frequencies of vibration.
Given: l1 – l2 = 2 mm (assuming l1 > l2), |n1 – n2| = 2 beats per second.
To Find: Frequencies n1 =? and n2 =?
Solution:
l1 + l2 = 1m = 1000 mm
Thus l1 = 501 mm and l2 = 499 mm
By law length n α 1/l
l1 > l2, hence n1 < n2
n2 – n1 = 2
n1 = n2 – 2
By law of length
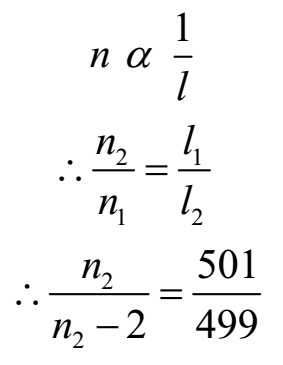
499 n2 = 501 n2 – 1002
1002 = 2 n2
n2 = 1002/2 = 501 Hz
n1 = n2 – 2 = 501 – 2 = 499 Hz
Ans: The frequencies of vibrations of two segments are 499 Hz and 501 Hz
Example 03:
A tuning fork of frequency 325 Hz is in unison with a sonometer wire of length 67 cm under certain tension. Find the number of beats heard per second when the length of the vibrating wire is decreased by 2 cm keeping the tension constant.
Given: l1 = 67 cm, l2 = 67 – 2 = 65 cm, Initial frequency = n1 = N = 325 Hz
To Find: |n1 – n2| =?
Solution:
By law length n α 1/l
l1 > l2, hence n1 < n2
By law of length
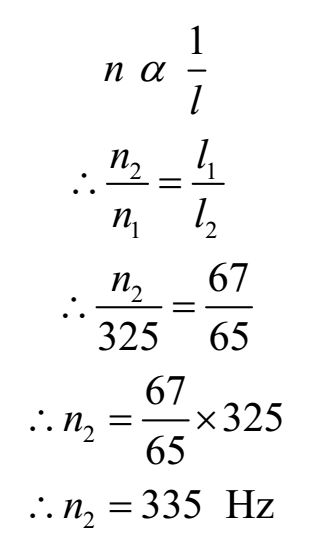
Number of beats = n2 – n1 = 335 – 325 = 10 per second
Number of beats = 10 per second
Ans: Number of beats heard 10 per second i.e. 10 Hz
Example 04:
A sonometer wire 0.60 m long resonates to a tuning fork. When its length is decreased by 5 cm, 10 beats per second are heard. Find the frequency of fork. If the mass per unit length of wire is 0.014 g cm-1, what is the tension?
Given: l1 = 0.60 m = 60 cm, l2 = 60 – 5 = 55 cm, |n1 – n2| = 10 per second, Mass per unit length = 0.014 g cm-1 = 0.014 x 10-1 kg m-1 = 1.4 x 10-3 kg m-1,
To Find: Frequency of fork = n1 = N =? Tension = T =?
Solution:
By law length n α 1/l
l1 > l2, hence n1 < n2
n2 – n1 = 10
n2 = n1 + 10
By law of length

55n1 + 550 = 60 n1
5n1 = 550
n1 = 110 Hz = N
Fundamental frequency of vibration of string is given by

Ans: Frequency of tuning fork 110 Hz, Tension in string is 24.39 N.
Example 05:
A sonometer wire under constant tension resonates with a tuning fork when the length of the wire is 65 cm. When the length of the wire is increased by one cm, 8 beats per second are heard with the same fork. Find the frequency of fork.
Given: l1 = 65 cm, l2 = 65 + 1 = 66 cm, |n1 – n2| = 8 per second.
To Find: Frequency of fork = n1 = N =?
Solution:
By law length n α 1/l
l1 < l2, hence n1 > n2
n1 – n2 = 8
n2 = n1 – 8
By law of length

66n1 – 528 = 65n1
n1 = 528 Hz
Ans: Frequency of tuning fork 528 Hz.
Example 06:
A stretched sonometer wire is in unison with a tuning fork. When the length of the wire is increased by two per cent, the number of beats heard per second is 5. Calculate the frequency of fork.
Given: Initial length = l1 cm, Final length = l2 = l1 + 2% l1 = 1.02 l1, |n1 – n2| = 5 per second.
To Find: Frequency of fork = n1 = N =?
Solution:
By law length n α 1/l
l1 < l2, hence n1 > n2
n1 – n2 = 5
n2 = n1 – 5
By law of length

1.02n1 – 5.1 = n1
0.02 n1 = 5.1
N1 = 5.1/0.02 = 255 Hz
Ans: Frequency of tuning fork 255 Hz.
Example 07:
A length of sonometer wire under constant tension when sounded with a tuning fork of higher frequency 271 Hz produced 5 beats per second. If the length of the wire is reduced by 5%, find the new frequency of the wire.
Given: Initial length = l1 cm, Final length = l2 = l1 – 5% l1 = 0.95 l1, n1 = N – 5 = 271 – 5 = 266 Hz.
To Find: New frequency of wire = n2 =?
Solution:
By law of length

Ans: New frequency of wire is 280 Hz.
Example 08:
When two tuning forks are sounded together, 5 beats per second are heard. One of the forks vibrates in unison with a sonometer wire of length 90 cm subjected to a given tension while the other fork vibrates with same wire of 91 cm length subjected to the same tension. Calculate the frequencies of tuning forks.
Given: Initial length = l1 = 90 cm, Final length = l2 = 91 cm, n1 = N1, n2 = N2, |N1 – N2| = 5 beats per second.
To Find: Frequencies of tuning forks, N1 =? = N2 =?
Solution:
By law length n α 1/l
l1 < l2, hence n1 > n2
N1 > N2
N1 – N2 = 5
N1 = N2 + 5
By law of length

91 N2 = 90 N2 + 450
N2 = 450 Hz
N1 = N2 + 5 = 450 + 5 = 455 Hz
Ans: Frequencies of tuning forks are 455 Hz and 450 Hz.
Example 09:
Two tuning forks when sounded together give 5 beats per second. One is in unison with a sonometer wire of length 1.20 m under constant tension. The other tuning fork is in unison with the same wire of length 1.25 m under identical conditions. Find the frequencies of the two forks.
Given: Initial length = l1 = 1.20 m, Final length = l2 = 1.25 m, n1 = N1, n2 = N2, |N1 – N2| = 5 beats per second.
To Find: Frequencies of tuning forks, N1 =? = N2 =?
Solution:
By law length n α 1/l
l1 < l2, hence n1 > n2
N1 > N2
N1 – N2 = 5
N1 = N2 + 5
By law of length

1.25 N2 = 1.20 N2 + 6
0.05 N2 = 6
N2 = 6/0.05 = 120 Hz
N1 = N2 + 5 = 120 + 5 = 125 Hz
Ans: Frequencies of tuning forks are 125 Hz and 120 Hz.
Example 10:
Two tuning forks when sounded together produce 5 beats per second. A sonometer wire of length 0.24 m is in unison with one of the forks. When the length of wire is increased by 1 cm, it is in unison with other fork. What are the frequencies of the tuning forks?
Given: Initial length = l1 = 0.24 m = 24 cm, Final length = l2 = 24 + 1 = 25 cm, n1 = N1, n2 = N2, |N1 – N2| = 5 beats per second.
To Find: Frequencies of tuning forks, N1 =? = N2 =?
Solution:
By law length n α 1/l
l1 < l2, hence n1 > n2
N1 > N2
N1 – N2 = 5
N1 = N2 + 5
By law of length

25 N2 = 24 N2 + 120
N2 = 120 Hz
N1 = N2 + 5 = 120 + 5 = 125 Hz
Ans: Frequencies of tuning forks are 125 Hz and 120 Hz.
Example 11:
A length of 34 cm of a sonometer wire gives 5 beats per second with a tuning fork. It again gives 5 beats per second when the length of the wire is increased to 35 cm. What is the frequency of fork?
Given: Initial length = l1 = 34 cm, Final length = l2 = 35 cm,
To Find: Frequency of tuning fork, N =?
Solution:
By law length n α 1/l
l1 < l2, hence n1 > n2
Now fork gives 5 beats per second in both cases
Hence, n1 > N > n2
n1 – N = 5 i.e., n1 = N + 5
N – n2 = 5 i.e., n2 = N – 5
By law of length

35N – 175 = 34N + 170
N = 345 Hz
Ans: Frequency of tuning fork is 345 Hz.
Example 12:
A tuning fork when sounded with a stretched sonometer wire produces 6 beats per second with the vibrating wire when its length is 95 cm or 100 cm. Find the frequency of the tuning fork.
Given: Initial length = l1 = 95 cm, Final length = l2 = 100 cm,
To Find: Frequency of tuning fork, N =?
Solution:
By law length n α 1/l
l1 < l2, hence n1 > n2
Now fork gives 5 beats per second in both cases
Hence, n1 > N > n2
n1 – N = 6 i.e., n1 = N + 6
N – n2 = 6 i.e., n2 = N – 6
By law of length

100N – 600 = 95N + 570
5N = 1170
N = 234 Hz
Ans: Frequency of tuning fork is 234 Hz.