Einstein’s Photoelectric Equation

Science > Physics > Photoelectric Effect >Einstein’s Photoelectric Equation

In this article, we shall, derive Einstein’s photoelectric equation and study its use to verify the characteristics of the photoelectric effect of light.

Wave Nature of Light:

Christian Huygen’s proposed that the light is propagated in the form of a wave. But this theory has a serious drawback. It was not able to explain the propagation of light in a vacuum. This drawback was removed by Maxwell he proposed that light is an electromagnetic wave and for the propagation of electromagnetic waves no material medium is required. Thus the wave nature of light was established.

Wave theory was able to explain all the phenomena associated with the propagation of light. But it failed to explain the energy distribution and modern phenomenon like photoelectric effect, Crompton effect, etc.

Particle Nature of Light:

Max Planck proved that the propagation of light or energy takes place in the form of packets of energy called quanta. Quantum of light is called a photon and thus he established the particle nature of light. Using particle or quantum nature of radiation we can explain the phenomenon of photoelectric effect and Crompton effect.

Planck’s Quantum Theory:

The quantum theory was proposed by Max Planck. According to this theory, radiation from a source is not emitted continuously, but it is emitted in packets or bundles of energy.  These packets are called quanta or photons. If the radiation is of frequency ν, each quantum has energy where h is Planck’s constant.

Thus energy of photon = E = hν

The energy is emitted in a discontinuous manner.  This is contrary to the classical theory which assumes that emission of energy is a continuous process.

Particle Nature of Electromagnetic Radiations:

In the interaction of radiation with matter, the radiation behaves as if it is made up of particles. These particles are called photons. Each photon has energy which is given by

E = hν = hc/λ

All photons of light of particular frequency (Wavelength) has the same amount of energy associated with them. The increase in the intensity of light increases the number of photons per second through a given area, but the energy of each photon will be the same. Photons are electrically neutral and are unaffected by electric or magnetic fields. Photons travel in a straight line with the speed of light ‘c’ but show diffraction in certain conditions.

The momentum of each photon is given by

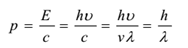
The wavelength of photon changes with the media, hence they have different velocities in different media. The rest mass of a photon is zero. Its kinetic mass is given by

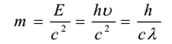
In photon particle collision (such as a photon-electron collision) the total energy and momentum are conserved. However, the number of photons may not be conserved in a collision. The photon may be absorbed or a new photon may be created.

Einstein’s Photoelectric Equation:

On the basis of Planck’s quantum theory, Einstein derived an equation for the photoelectric effect known as Einstein photoelectric equation. Einstein assumed that

• Light consists of photons or quanta of energy, energy in each photon is hν. Where h is the Planck’s constant and ν is the frequency of light
• Each incident photon collides with an electron inside an atom and gives all its energy to the electron.
• Part of this energy is used by the electron to come out of the surface of the metal and the remaining part is the kinetic energy with which the electron is emitted.
• The minimum energy required by an electron to come out of the surface of the metal is called the photoelectric work function (∅_o) of the metal.
• The remaining energy (hν – ∅_o) is the maximum kinetic energy of the electron with which a photoelectron will be ejected.

Thus, Maximum kinetic energy of electron = energy of photon – work function

Let ‘m’ be the mass of electron and v_max be the maximum velocity of photo-electron by which it will be ejected.

This equation is known as Einstein’s photoelectric equation

Photoelectric Work Function:

In the photoelectric effect, the most loosely attached electron of an atom of photosensitive material is removed. The minimum energy required to free an electron from the given surface is called the photoelectric work function (∅_o) of the material of the surface. The work function is a characteristic property of the metal surface.

Mathematically work function is given by

∅_o = h ν_o

Where ν_o = Threshold frequency and h = Planck’s constant.

Explanation of the Existence of Threshold Frequency on the Basis of Einstein’s Photoelectric Equation:

For a given metallic surface, photo-electrons are emitted only when the frequency of incident light is greater than or equal to a certain minimum frequency (no) known as the threshold frequency. The threshold frequency is different for different Substances,

By Einstein’s photoelectric equation

Where ν_o  = Threshold frequency and h = Planck’s constant and 

ν =  frequency of incident radiation

The kinetic energy is always non-negative quantity i.e. it may either be positive or zero thus

Which indicates that for the photoelectric effect, the frequency of incident radiation or incident photon should be equal to or greater than the threshold frequency. The attractive force acting on probable photoelectrons in different atoms is different. Therefore the threshold frequency is different for the different substances.

Explanation of the Effect of Intensity on the Basis of Einstein’s Photoelectric Equation:

If the frequency of incident light is less than the threshold frequency, photoelectrons are not emitted, however large the intensity of incident light may be.

The number of photo-electrons emitted per second is directly proportional to the intensity of incident light.  Thus the photoelectric current is directly proportional to the intensity of incident light. If the intensity of light is more, the number of incident photons on the surface are more. Due to the increased number of photoelectron the rate of photoemission increases, hence the strength of photoelectric current increases. Thus we can conclude that the photoelectric effect (current) is directly proportional to the intensity of incident radiation.

Explanation of the Possible Maximum Kinetic Energy on the Basis of Einstein’s Photoelectric Equation:

By Einstein’s photoelectric equation

Where ν_o  = Threshold frequency and h = Planck’s constant and 

ν =  frequency of incident radiation

This equation does not contain the term of intensity, thus we can say that the maximum kinetic energy of photoelectron is independent of the intensity of incident radiation but depends upon the frequency of incident radiation. This equation indicates that the maximum kinetic energy of the electron depends upon the frequency of incident radiation. And if the frequency of incident radiation is increased kinetic energy of photoelectron also gets increased.

Explanation of Instantaneity of Photoelectric Effect on the Basis of Einstein’s Photoelectric Equation:

The photoelectric effect is an instantaneous process. There is no time lag between the incidence of light and the emission of the photo-electrons in other words, the surface begins to emit photo-electrons as soon as light falls on it.  Also the emission of photo-electrons stops the moment incident light is cut off.

When radiation is incident on the photo-emitting surface at that instant, the whole energy of the photon is transferred to a single electron in one go. Thus the electron gets emitted without any time lag and the photoelectric effect is the instantaneous process.

Previous Topic: Numerical Problems on Photoelectric Effect

Next Topic: Numerical Problems on Photoelectric Equation

Science > Physics > Photoelectric Effect >Einstein’s Photoelectric Equation