Numerical Problems on Beats – 02

Science > Physics > Wave Motion > Numerical Problems on Beats

In the last article, we have studied numerical problems on beats involving the sounding of two tuning forks. In this article, we shall study numerical problems on beats involving the sounding of two sound notes.

Example – 01:

Two sound waves having wavelengths of 87 cm and 88.5 cm when superimposed produce 10 beats per second. Find the velocity of sound.

Given: Wavelength of first wave = λ₁ = 87 cm = 87 × 10^-2 m, Wavelength of second wave = λ₂ = 88.5 cm = 88.5 × 10^-2 m, No. of beats = 10 per second.

To Find: Velocity of sound = v =?

Solution:

We have v= n λ, Hence n = v/ λ

Now n ∝ 1/ λ   given λ₂ >   λ₁ Hence n₁ >   n₂

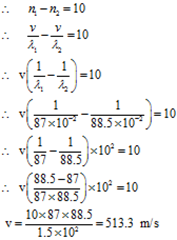
Ans:  Velocity of sound 513.3 m/s

Example – 02:

Wavelengths of two sound waves in a gas are 2.0 m and 2.1m respectively. They produce 8 beats per second when sounded together. Calculate the velocity of sound in the gas and the frequencies of the two waves.

Given: Wavelength of first wave = λ₁ = 2.0 m, Wavelength of second wave = λ₂ = 2.1m, No. of beats = 8 per second.

To Find: Velocity of sound = v =? Frequencies of notes =?

Solution:

We have v= n λ, Hence n = v/ λ

Now n ∝ 1/ λ   given λ₂ >   λ₁ Hence n₁ >   n₂

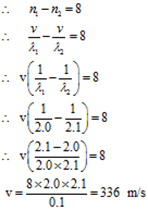
Now n₁ = v/λ₁ = 336 /2.0 = 168 Hz and

n₂ = v/λ₂ = 336 /2.1 = 160 Hz

Ans:  Velocity of sound 336 m/s, the frequencies of notes are 168 Hz and 160 Hz.

Example – 03:

Two sound waves of lengths 1m and 1.01m produce 6 beats in two seconds when sounded together in the air. Find the velocity of sound in air.

Given: Wavelength of first wave = λ₁ = 1 m, Wavelength of second wave = λ₂ = 1.01m, No. of beats = 6 per two second = 3 per second.

To Find: Velocity of sound = v =?

Solution:

We have v= n λ, Hence n = v/ λ

Now n ∝ 1/ λ   given λ₂ >   λ₁ Hence n₁ >   n₂

Ans:  Velocity of sound 303 m/s

Example – 04:

Two tuning forks of frequencies 320 Hz and 340 Hz produce sound waves of lengths differing by 6cm in a medium. Find the velocity of sound in the medium.

Given: Frequency of first wave = n₁ = 320 Hz, Frequency of second wave = n₂ = 340 Hz, Difference in wavelengths = 6 cm = 6 × 10^-2 m

To Find: Velocity of sound = v =?

Solution:

We have v= n λ, Hence λ = v/ n

Now λ ∝ 1/ n   given n₂ >   n₁ Hence λ₁ > λ₂

Ans:  Velocity of sound 326.4 m/s

Example – 05:

Wavelengths of two sound waves in air are 81/174m and 81/175 m. When these waves meet at a point simultaneously, they produce 4 beats per second. Calculate the velocity of sound in air.

Given: Wavelength of first wave = λ₁ = 81/174 m, Wavelength of second wave = λ₂ = 81/175 m, No. of beats = 4 per second.

To Find: Velocity of sound = v =?

Solution:

We have v= n λ, Hence n = v/ λ

Now n ∝ 1/ λ   given λ₁ >   λ₂ Hence n₂ >   n₁

Ans:  Velocity of sound 324 m/s

Example – 06:

Wavelengths of two sound waves in air are 81/173m and 81/170 m. When these waves meet at a point simultaneously, they produce 10 beats per second. Calculate the velocity of sound in air.

Given: Wavelength of first wave = λ₁ = 81/173 m, Wavelength of second wave = λ₂ = 81/170m, No. of beats = 10 per second.

To Find: Velocity of sound = v =?

Solution:

We have v= n λ, Hence n = v/ λ

Now n ∝ 1/ λ   given λ₂ >   λ₁ Hence n₁ >   n₂

Ans:  Velocity of sound 270 m/s

Example – 07:

Wavelengths of two notes in the air are 70/153 m and 70 /157 m. Each of these notes produces 8 beats per second with the third note of fixed frequency. What are the velocity of sound in air and the frequency of the third note?

Given: Wavelength of first wave = λ₁ = 70/153 m, Wavelength of the second wave = λ₂ = 70/157 m, No. of beats with the third note = 8 per second.

To Find: Velocity of sound = v =? The frequency of the third note =?

Solution:

We have v= n λ, Hence n = v/ λ

Now n ∝ 1/ λ   given λ₁ >   λ₂ Hence n₂ >   n₁

Let n be the frequency of the third note, such that n₂ > n >   n₁

Given n₂ – n   = 8 ………. (1)

and n  –  n₁= 8  ………. (2)

Adding equations (1) and (2) we get

Now n₁ = v/λ₁ = 280 /(70/153) = 4 × 153 = 612 Hz

and n  = n₁ + 8 = 512 + 8 = 520 Hz

Ans:  Velocity of sound 280 m/s and frequency of the third note is 620 Hz.

Example – 08:

Wavelengths of two notes in the air are 80/179 m and 80/177 m. Each note produces 4 beats per second with the third note of fixed frequency. Calculate the velocity of sound in air.

Given: Wavelength of the first wave = λ₁ =80/179 m, Wavelength of the second wave = λ₂ = 80/177 m, No. of beats with the third note = 4 per second.

To Find: Velocity of sound = v =?

Solution:

We have v= n λ, Hence n = v/ λ

Now n ∝ 1/ λ   given λ₁ <   λ₂ Hence n₁ >   n₂

Let n be the frequency of the third note, such that n₁ > n >   n₂

Given n₁ – n   = 4 ………. (1)

and n  –  n₂= 4  ………. (2)

Adding equations (1) and (2) we get

Ans:  Velocity of sound 320 m/s

Previous Topic: More Numerical Problems on Beats

Next Topic: Doppler Effect in Sound

Science > Physics > Wave Motion > Numerical Problems on Beats