Total Internal Reflection of Light

Science > Physics > Refraction of Light > Total Internal Reflection of Light

In this article, we shall study the phenomenon of total internal reflection and its applications.

Total Internal Reflection of Light and its Explanation:

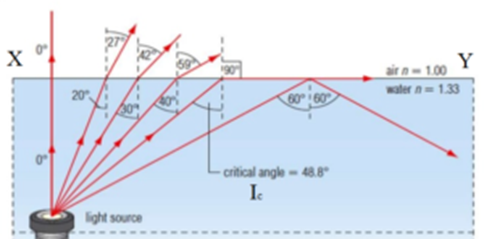
Let us consider a point source O in a denser medium (Water). Let XY be the boundary separating the denser medium (Water) and the rarer medium (Air). As the angle of incidence increases, the angle of refraction also increases. At a particular angle of incidence i_C, the angle of refraction is 90° and hence the refracted ray moves along the surface of water i.e. along XY. If the angle of incidence is more than i_C, there is no refracted ray, the incident ray is completely reflected back in the water. This phenomenon is known as total internal reflection.

In such cases the intensity of incident ray and the intensity of reflected ray are the same, hence the image obtained in total internal reflection are brighter. In the case of a mirror, some energy from incident ray is absorbed by the mirror, surface hence the intensity of reflected ray is less than the incident ray. Hence the images obtained from the mirror are somewhat dull

Critical angle:

When the angle of refraction in rarer medium (air) is 90°, the angle of incidence in the denser medium (water) is called the critical angle for the material. It is denoted by i_C. It is the minimum angle of incidence when the total internal reflection of light takes place

The critical angle for the glass-air interface is maximum for red colour and minimum for violet colour.

Conditions for Total Internal Reflection of Light:

• The ray of light should travel through an optically denser medium into an optically rarer medium.
• The angle of incidence should be equal or greater than the critical angle (i_C) for the two mediums.

To Show  sin i_C = 1/ ₂μ₁

By Snell’s law

₁μ₂ = sin i /sin r

By the principle of reversibility of light, we can write

₂μ₁ = sin r /sin i

At total internal reflection, i = i_C and the angle of refraction r = 90°

₂μ₁ = sin 90° /sin i_C

∴ ₂μ₁ = 1 /sin i_C

∴ sin i_C   = 1 / ₂μ₁    (Proved as required)

Numerical Problems on Critical Angle:

Example – 01:

The critical angle for the air-glass interface is 45°. Find the refractive index of the glass.

Given: Critical angle = i_C = 45°.

Fo find: Refractive index of glass = μ =?

Solution:

∴ μ = 1 /sin i_C =  1/sin45° = 1 / 0.707 =  1.414

Ans:  The refractive index of glass is 1.414

Example – 02:

The critical angle for a medium is 40°. Find the refractive index of the medium.

Given: Critical angle = i_C = 40°.

Fo find: Refractive index of medium = μ =?

Solution:

∴ μ = 1 /sin i_C =  1/sin40° = 1 / 0.6428 =  1.56

Ans:  The refractive index of medium is 1.56

Example – 03:

Find critical angle of water air interface. Given _an_w = 4/3 = n.

Given: refractive index of water w.r.t. air = _an_w = 4/3

Fo find: Critical angle = i_C =?

Solution:

∴ 4/3 = 1 /sin i_C 

∴ sin i_C = 3/4 = 0.75

∴   i_C = sin^-1(0.7500) = 48°36′

Ans:  The critical angle for water air interface is   48°36′.

Applications of Total Internal Reflection of Light:

• The phenomenon of total internal reflection of light is used in many optical instruments like telescopes, microscopes, binoculars, spectroscopes, periscopes etc.
• The brilliance of a diamond is due to total internal reflection.
• Optical fibre works on the principle of total internal reflection.
• This phenomenon is used in many optical instruments like telescopes, microscopes, binoculars, spectroscopes, periscopes etc.
• The phenomenon of mirage can be explained on the basis of total internal reflection.

Sparkling Brilliance of Diamond:

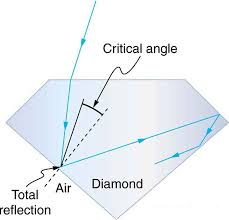
Total internal reflection of the light phenomenon is also used in polishing of diamonds, to create a sparkling brilliance effect. Sparkling brilliance of diamond can be explained as follows

For diamond and air interface the difference between the refractive index of a diamond (μ = 2.8) and the refractive index of air (μ = 1)  is very large. The critical angle for a diamond in diamond and air interface is very small (24.4°).

By polishing the diamond with specific cuts it is adjusted that most of the light rays approaching surface are incident with the angle of incidence more than the critical angle. Hence they suffer multiple total internal reflections and ultimately come out of diamond from the top. This gives the diamond a sparkling brilliance.

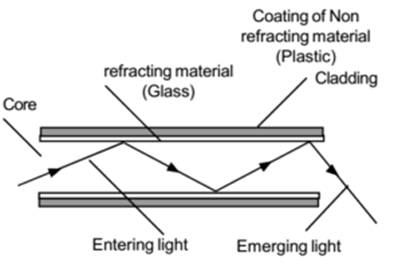
Optical Fibre:

When light enters the core of glass fibre from one end with such that the angle of incidence is greater than critical angle then, it suffers total internal reflection of light many times and emerges out as the divergent beam from another end. This is known as the principle of the optical fibre.

Each fibre is made up of a material of high refractive index. Its outer side is covered by a layer of material of low refractive index, which provides a suitable boundary. Due to this, the transmission of light from one fibre to others is avoided.

The glass is not flexible and hence breaks easily. Hence the optical fibres are grouped together in a single cable, which is flexible and unbreakable.

Applications of optical fibre:

• It is used in optical communication.
• It is used in endoscopy.

Use of optical fibre  for communication:

Electrical or radio signals are converted into optical signals by modulating laser light. These signals enter one end of the optical fibre and are transmitted through it by total internal reflection to the desired place. At this end, these optical signals are again converted into electrical or radio signals.

Compared to copper cable,  loss of intensity of the signal is almost negligible. Besides many signals can be transmitted simultaneously.

Mirage:

A mirage is an optical phenomenon that creates the illusion of water and results from the refraction of light through a non-uniform medium.  Mirages are most commonly observed on sunny days when driving down a roadway. As you drive down the roadway, there appears to be a puddle of water on the road several metres (maybe one-hundred metres) in front of the vehicle. Of course, when you arrive at the perceived location of the puddle, you recognize that the puddle is not there.  The appearance of the water is simply an illusion.

Explanation of mirage can be given on the basis of total internal reflection of the light phenomenon. Mirages occur on sunny days. The role of the sun is to heat the roadway to high temperatures. This heated roadway, in turn, heats the surrounding air, keeping the air just above the roadway at higher temperatures than that day’s average air temperature. Hot air tends to be less optically dense than cooler air. As such, a non-uniform medium has been created by the heating of the roadway and the air just above it.

While light will travel in a straight line through a uniform medium, it will refract when travelling through a non-uniform medium. If a driver looks down at the roadway at a very low angle (that is, at a position nearly one hundred yards away), light from objects above the roadway will follow a curved path to the driver’s eye as shown in the diagram. Now, the observer receives two rays from the object, one direct and other curved. Thus the illusion of water takes place.

Reflecting Prisms in Periscope and Binoculars:

It works on the principle of total internal reflection of the light phenomenon. In periscope, we use the totally reflecting prisms which turn the ray through 90°.  A totally reflecting prism is that which has one of its angle equal to 9° and each of the remaining two angles equal to 45°.

If a ray of light from an object strikes one of its faces at a right angle, it enters the prism without any change of direction and meets the hypotenuse at an angle of 45°, so the angle of incidence is also 45°. As the angle of incidence is greater than the critical angle of the glass which is 42°, the ray will be totally reflected, the angle of reflection is 45°. Now this reflected light strikes the faces of the second prism at a right angle, it enters the prism without any change of direction and meets its hypotenuse at an angle of 45°, so the angle of incidence is also 45°. Again due to total internal reflection of light is reflected by the angle of reflection 45° towards the eye of the observer.

The image obtained using the total internal reflection of light is clear and bright due to almost no loss of intensity.

Prismatic binoculars:

Science > Physics > Refraction of Light > Total Internal Reflection of Light