Science > Chemistry > Solid State > Bravais Lattices
In this article, we shall study the structures of Bravais Lattices.
A crystal is a homogenous portion of a solid substance made of a regular pattern of structural units bonded by plane surfaces making a definite angle with each other.
Unit Cell:
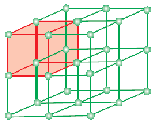
A unit cell is the smallest structural repeating unit of crystalline solid (space lattice). When unit cells of the same crystalline substance are repeated in space in all directions, a crystalline solid is formed. The unit cell is represented on paper by drawing lines connecting centres of constituent particles.
The geometrical form consisting only of a regular array of points in space is called lattice or space lattice. It may be defined as an array of points showing how molecules, atoms or ions are arranged in different sites, in a three-dimensional space. Each point at the intersection of lines in the unit cell represents constituent particle viz. molecule or atom or ion. This point of intersection of lines in the unit cell is called lattice point or lattice site.
Note: Each lattice point in the crystal lattice has the same surroundings or environment. Two or more crystalline substance may have the same lattice space. Each and every particle in the array is always represented by a lattice point in the three-dimensional array.
Characteristics of Crystal Lattice:
- The crystal lattice is a regular arrangement of constituent particles of a crystalline solid in three-dimensional space.
- It consists of a large number of unit cells.
- The crystal lattice is defined in terms of properties of the unit cell.
- On break up, it forms numerous unit cells.
- A crystal lattice can be obtained, handled and studied in a laboratory during experiments.
- It is a macroscopic property.
Characteristics of Unit Cell:
- A unit cell is the smallest structural repeating unit of crystalline solid.
- It is the fundamental unit of crystal lattice which possesses all the properties of the crystal.
- Unit cell defines fundamental properties crystal lattice.
- Unit cells are a fundamental unit, hence can not be divided further.
- A unit cell is hypothetical concept Hence it can not be obtained during experiments.
- It is a microscopic property.
Types of Space Lattice:
One Dimensional Lattice:
In this lattice, there exists a set of points arranged at equal distances along.

Two Dimensional Lattice:
In this type, two sides and the angle between them is specified. There are five types of two-dimensional lattice.
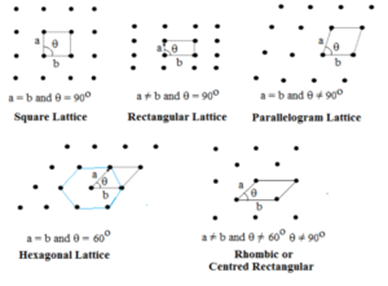
Hexagonal lattice is a rhombus with θ = 60°
Bravais Lattices:

Let lengths of three edges of the unit cell be a, b, and c. Let α be the angle between side b and c. Let β be the angle between sides a and c. Let γ be the angle between sides a and b.
French mathematician Bravais said that for different values of a, b, c, and α, β, γ, maximum fourteen (14) structures are possible. These arrangements are called Bravais Lattices.
14 Bravais Lattices:
|
Sr. No. |
Crystal
System |
Space Lattice
Type |
Diagram |
Edge Lengths |
Angles |
Examples |
|
1 |
Cubic |
Simple
primitive |
 |
a = b = c |
α = β = γ = 90° |
Polonium (Po) |
|
2 |
Cubic |
Body centred |
 |
a = b = c |
α = β = γ = 90° |
Iron (Fe), Rubidium (Rb), Sodium (Na), Titanium (Ti), Tungsten (W), Uranium (U), Zirconium (Zr) |
|
3 |
Cubic |
Face centred |
 |
a = b = c |
α = β = γ = 90° |
Copper (Cu), Aluminium (Al), Nickel (Ni), Gold (Au), Silver (Ag), Platinum (Pt) |
|
4 |
Tetragonal |
Simple
primitive |
 |
a = b ≠ c |
α = β = γ = 90° |
SnO2 |
|
5 |
Tetragonal |
Body centred |
 |
a = b ≠ c |
α = β = γ = 90° |
Ti, O2, CaSO4 |
|
6 |
Orthorhombic |
Simple
primitive |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
Rhombic sulphur |
|
7 |
Orthorhombic |
Body centred |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
KNO3 |
|
8 |
Orthorhombic |
Face centred |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
BaSO4 |
|
9 |
Orthorhombic |
End centred |
 |
a ≠ b ≠ c |
α = β = γ = 90° |
MgSO4, 7H2O |
|
10 |
Monoclinic |
simple
primitive |
 |
a ≠ b ≠ c |
α =γ = 90° and β ≠ 90° |
Monoclinic sulphur |
|
11 |
Monoclinic |
End centred |
 |
a ≠ b ≠ c |
α =γ = 90° and β ≠ 90 |
Na2SO4. 10H2O |
|
12 |
Triclinic |
simple
primitive |
 |
a ≠ b ≠ c |
α =γ = 90° and β ≠ 90° |
K2Cr2O7, H3BO3 |
|
13 |
Hexagonal |
Simple
primitive |
 |
a = b ≠ c |
α = β = 90°
and γ = 120° |
ZnO,
BeO, CoS, SnS |
|
14 |
Rhombohedral |
Simple
primitive |
 |
a ≠ b ≠ c |
α = β = γ ≠ 90° |
Calcite, NaNO3, FeCO3 |
Particle at Corner:

The particle at the corner of the unit cell is shared by 8 unit cells (4 layers below and 4 layers above). Hence each unit cell 1/8 particle.
Particle at Face:

The particle at the face of the unit cell is shared by 2 adjacent unit cells. Hence each unit cell 1/2 particle.
Particle at Edge:

The particle at the edge of the unit cell is shared by 4 unit cells (2 layers below and 2 layers above). Hence each unit cell 1/4 particle.
Coordination Number:
The coordination number of the constituent particle of the crystal lattice is the number of particles surrounding a single particle in a crystal lattice.
More the coordination number more tightly the particles are packed in the crystal lattice. Coordination number is the measure of the hardness of the crystal.
Number of Particles in Unit Cell and coordination Number
Simple Cubic Structure (scc):

From the
structure, we can see that there are 8 particles at 8 corners of the unit cell.
Each corner particle is shared by 8 neighbouring unit cells. Hence each unit
cell contains 1/8 th of the particle at its corner.
Number of corners = 8, Hence number of particles in unit cell = 1/8
x 8 = 1
Each particle in this structure is directly in contact with four other particles in its plane and one particle each in the layer above and the layer below. Hence the coordination number for simple cubic structure is 4+ 1+ 1 = 6

Body-Centred Cubic Structure (bcc):

From the structure, we can see that there are 8 particles at 8 corners of the unit cell. Each corner particle is shared by 8 neighbouring unit cells. Hence each unit cell contains 1/8 th of the particle at its corner. Number of corners = 8, hence number of particles in unit cell at corners = 1/8 x 8 = 1
At the same time, there is an atom at the centre of the cell, Hence the number of particles in unit cell 1 + 1 = 2
Each particle in this structure is directly in contact with four other particles in the layer above and four particles in the layer below. Hence the coordination number for body centred cubic structure is 4 + 4 = 8

Face Centered Cubic Structure (fcc):

From the structure, we can see that there are 8 particles at 8 corners of the unit cell. Each corner particle is shared by 8 other neighbouring unit cells. Hence each unit cell contains 1/8 th of the particle at its corner. The number of corners = 8. Hence the number of particles in a unit cell at corners = 1/8 x 8 = 1
There are 6
particles at 6 faces of the unit cell. Each face particle is shared by 2
neighbouring unit cells. Hence each unit cell contains 1/2 of the particle at
its face.
The number of faces = 6. Hence the number of particles on face = 1/2 x 6 = 3
Hence number of particles in unit cell 1 + 3 = 4
Each particle in this structure is directly in contact with 4 other particles in its layer and with 4 particles in the layer above and 4 particles in the layer below. Hence the coordination number for face centred cubic structure is 4 + 4 + 4 = 12

Notes:
For edge centred particle it is shared by 4 unit cells. Hence each unit cell consists of 1/4 particle The number of atoms per unit cell is in the same ratio as the stoichiometry of the compound. Hence it helps to predict the formula of the compound.
Science > Chemistry > Solid State > Bravais Lattices
2 replies on “Bravais Lattices”
This really explain this topic in it’s simplest way.
Very nice explanation