Science > Physics > Wave Theory of Light > Polarization of Light
In this article, we shall study the concept of polarization of light, Brewster’s law associated with it.
Ordinary Light:
Light waves are transverse in nature. The direction of its vibration is in the plane which is perpendicular to the direction of propagation of the wave. Thus wave can vibrate in any plane (infinite possibilities) which is perpendicular to the direction of propagation of the wave. Such a light wave is called unpolarized light.
Transverse Nature of Light Waves:
The following phenomena prove the transverse nature of light.
- The intensity of light at a place changes continuously.
- Light can be polarized.
When light waves are passed through two crystalline slits say A and B (These slits are the tourmaline plates cut parallel to the axis of crystal). Ordinary light (say from the sun) is incident on the crystal A.
When crystal A and crystal B are parallel to each other, the intensity of the light emerging from crystal A is constant at any orientation of A and passes through crystal B without any change.
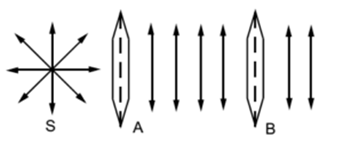
Now crystal B is rotated w.r.t. crystal A, the intensity of emerging light from crystal B decreases and becomes zero when crystal B is at right angle w.r.t crystal A.
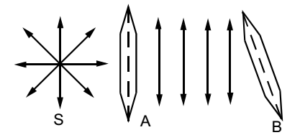
This experiment proves the transverse nature of the light waves. Crystal A is called polarizer and crystal B is called analyzer.
Plane Polarized Light:
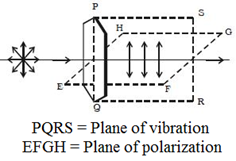
When the transverse vibrations of the light wave are confined to a plane containing the direction of propagation, the light is said to be plane-polarized. The plane in which the vibration lie is called the plane of vibration. The plane perpendicular to the plane of vibration is called the plane of polarization and the light is said to be polarized in it. In this plane the vibrations of light are absent.
Schematic Representation of Light:

Polarized light:
When the transverse vibrations of the light wave are confined to a plane containing the direction of propagation, the light is said to be plane-polarized.
Plane of vibration:
The plane in which the vibrations of polarized light takes place is called the plane of vibration.
Plane of polarization:
The plane perpendicular to the plane of vibration in which there are no vibrations of polarized light is called the plane of polarization.

Polarization:
The phenomenon of restriction of the vibrations of light waves in a particular plane perpendicular to the direction of propagation of wave motion is called polarization.
Polarizer:
The substances which bring about the plane polarization of light are called as polarisers. e.g. Tourmaline crystal, Nicol prism.
Unpolarized light:
Light waves are transverse in nature. The direction of a light in which the vibrations of the electric vectors are in all possible directions, which are perpendicular to the direction of propagation
Unpolarized light:
Light waves are transverse in nature. The direction of a light in which the vibrations of the electric vectors are in all possible directions, which are perpendicular to the direction of propagation of the wave is called unpolarized waves.
Plane of Incidence:
The plane containing the incident and reflected rays and normal to the surface is called the plane of incidence.
Diagram Showing Partial Polarization:

Malus showed that when a beam of unpolarized light is reflected from a nonmetallic surface, the reflected light is partially plane-polarized. The degree of polarization depends on the angle of incidence. The particular angle of incidence at which the reflected light is completely plane polarized is called the angle of polarization or polarizing angle. The vibrations of the reflected plane-polarized light are found to be perpendicular to the plane of incidence.
Distinguishing between Polarized Light and Unpolarized Light:
| Polarized Light | Unpolarized Light |
| When the vibrations of electric vectors are confined in one plane, the light is called plane polarized light. | The wave in which the electric vector can vibrate in any plane (infinite possibilities) which is perpendicular to the direction of propagation of the wave is called unpolarized light. |
| The x– and y– components of the electric field have a constant phase difference between them. | The phase difference between the components of the electric field does not exist, and the changes in the electric field take place at random speeds. |
| Can be obtained from sunlight | Can be obtained by reflection and scattering |
| Cannot be converted intp unpolarized light | Can be converted into polarized light with the decrease in the intensity. |
Brewster’s law:
The tangent of the polarizing angle is equal to the refractive index of the material of the surface from which reflection is taking place.
Mathematically, μ = tan ip
This polarizing angle is the characteristic of the medium.

ip = angle of incidence and r = angle of refraction
Proof:
Let us consider the unpolarized monochromatic light incident in the air at the polarizing angle ip on the plane surface XY of the transparent medium of refractive index μ. Experimentally Brewster proved that ∠ SQR = 90°.

Brewster further proved that the polarizing angle is a function of a wavelength of the light. This law is not obeyed by polished metallic surfaces.
To prove that at the polarizing angle the reflected ray and refracted ray are mutually perpendicular.

ip = angle of incidence and r = angle of refraction

Numerical Problems:
Example – 01:
Find the refractive index of glass if the angle of incidence at which the polarization of light reflected from the surface of the glass is 58°.
Given: the polarization angle = ip = 58°
To Find: Refractive index of the medium = μ = ?
Solution:
μ = tan ip = tan 58° = 1.6003
Ans: Refractive index of the medium is 1.6003
Example – 02:
In a glass plate of refractive index is 1.732 is to be used as a polarizer, what would be the polarizing angle and angle of refraction.
Given: Refractive index of the medium = μ = 1.732
To find: polarising angle = ip = ?, angle of refraction = r =?
Solution:
μ = tan ip = 1.732
∴ ip = tan-1(1.732) = 60°
By snell’s law
μ = sini/sinr
sin r = sini/μ = sin 60°/1.732 = 0.8660/1.732 = 0.5
∴ r = sin-1(0.5) = 30°
Ans: Polarizing angle is 60° and angle of refraction is 30°
Example – 03:
A ray of light travelling through air, falls on the surface of a glass slab at an angle i. it is found that the angle between the reflected and refracted ray is 90°. If the speed of light in glass is 2 x 108 m/s, find the angle of incidence. c = 3 x 108 m/s.
Given: angle between the reflected and refracted ray is 90°, speed of light in glass is = cg = 2 x 108, speed of light in air = ca = 3 x 108 m/s
To find: angle of incidence = i = ?
Solution:
The refractive index of glass is given by
μg = ca/cg = 3 x 108 / 2 x 108 = 1.5
Now the angle between the reflected and refracted ray is 90°
Hence the angle of incidence is equal to the angle of polarization.
μ = tan ip = 1.5
∴ ip = tan-1(1.5) = 56°19′
Ans: Angle of polarization is 56°19′
Example – 04:
If the critical angle of the medium is sin-1 (3/5), find the polarizing angle.
Given: Critical Angle = ic = sin-1 (3/5)
To Find: Polrizing angle = ip = ?
Solution:
ic = sin-1 (3/5)
Sin ic = 3/5
Refractive index = μ = 1/ Sin ic = 5/3
μ = tan ip = 5/3
∴ ip = tan-1(5/3) = 56°19′
Ans: Angle of polarization is 59°2′
Previous Topic: Numerical Problems on wave Theory of Light
Next Topic: Polaroids and Their Applications