Science > Physics > Rotational Motion > Concept of Moment of Inertia
In this article, we are going to study important physical quantity related to the rotational motion of the body called the moment of inertia and its significance.
Rigid Body:
A rigid body is one whose geometric shape and size remains unchanged under the action of any external force.
Axis of rotation:
When a rigid body performs the rotational motion, the particles of the body moves in circles. The centres of these circles lie on a straight line called the axis of rotation, which is fixed and perpendicular to the plane of circles. The particles on the axis of rotation are stationary.
Moment of Inertia:
The moment of inertia of a rigid body about a given axis is, defined as the sum of the products of the mass of each and every particle of the body and the square of its distance from the given axis.
S.I. unit of moment of inertia is kg m² and C.G.S. system it is g cm². Dimensions of the moment of inertia are [M1L2T0]
Explanation:
If the system of masses consists of a number of point masses m1, m2, m3, m4, …….., mn situated at a distance of r1, r2, r3, r4, …….., rn from the axis of rotation, then by definition of the moment of Inertia we have
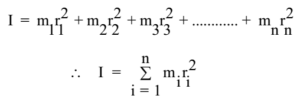
Instead of assuming the body to be composed of discrete masses, it can be considered to be composed of continuous matter (mass); then the process of summation should be replaced by integration with proper limits.
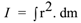
Physical Significance of Moment of Inertia:
Newton’s first law of motion is also called a law of inertia indicates that a body is unable to change by itself its state of rest or state of uniform motion along a straight line. This property of inertness is known as inertia. It is an inherent property of matter. It is due to the inertia, a body opposes any change in its state of rest or of uniform motion in a straight line.
In the translational motion, the mass of a body is a measure of its inertia. Greater the mass, larger is the inertia, greater is the force required to produce a given linear acceleration in it. In rotational motion, the moment of inertia of a body is a measure of its inertia. Greater the moment of inertia, larger is the torque required to produce a given angular acceleration in it.
Thus the moment of inertia in the rotational motion is analogous to the mass in translational motion because it plays the same role in rotational motion as the mass plays in translational motion. This is clear from the following table
| Sr.No. | Translational motion | Rotational motion |
| 1 | Linear Momentum p = m v | Angular Momentum L = Iω |
| 2 | Force F = m a | Torque τ = Iα |
| 3 | Kinetic Energy K.E. = ½mv² | Kinetic Energy K.E. = ¼mv² |
Radius of Gyration:
The radius of gyration of a rigid body about a given axis is defined as the distance from the axis at which the whole mass of the body must be supposed to be concentrated so that this imaginary point mass has the same moment of Inertia as the actual body, about the given axis.
The radius of gyration is denoted by letter ‘K’. As it is a distance, its S.I. unit is m and c.g.s. unit is cm. Its dimensions are [M0L1T0]
The expression for moment of inertia in terms of the radius of gyration is
I = MK².
Where I = Moment of inertia of a body
M = Mass of the body
K = Radiation of gyration of the body
Physical Significance of Radius of Gyration:
Moment of inertia depends on the mass of the body, the distribution of mass about the axis of rotation and the position of the axis of rotation. These factors can be separated by expressing the moment of inertia as a product of the mass and the square of a particular distance from the axis of rotation. This particular distance is called a radius of gyration (K) of the body. By definition of the radius of gyration

From the above explanation, we can conclude that the radius of gyration is the measure of the distribution of the mass of the body about the given axis
Numerical Problems on Definition of Moment of Inertia:
Example 01:
Four point masses 1kg, 2 kg, 3 kg and 4 kg are located at the corners A, B, C and D of a square ABCD of side 1m. Find the moment of inertia and radius of gyration in each of the following cases when the axis of rotation is
- passing through A and perpendicular to the plane of ABCD
- passing through O, the centre of the square and perpendicular to plane of ABCD
- along the side AB
- along diagonal AC
Given: m1 = 1 kg, m2 = 2 kg, m3 = 3 kg, m4 = 4 kg, AB = BC = CD = AD = 1 m
Solution:
Axis passing through A and perpendicular to the plane of ABCD

| Sr. No. | Mass | Distance from A |
| 1 | m1 = 1 kg | r1 = 0 |
| 2 | m2 = 2 kg | r2= 1 m |
| 3 | m3 = 3 kg | r3= √2 m |
| 4 | m4 = 4kg | r4 = 1m |
IA = ∑ miri² = m1r1² + m2r2² + m3r3² + m4r4²
∴ IA = (1)(0)² + (2)(1)² + (3)(√2)² + (4)(1)²
∴ IA = 0 + 2 + 6 + 4 = 10 kg m²
M = m1 + m2 + m3 + m4 = 1 + 2 +3 + 4 = 10 kg
By definition of radius of gyration
IA = MKA²
∴ 10 = 10 KA²
∴ KA² = 1
KA = 1 m
Ans: Moment of inertia of system about axis passing through A and perpendicular to the plane of ABCD is 10 kg m² and corresponding radius of gyration is 1 m.
Axis passing through O, the centre of the square and perpendicular to the plane of ABCD

| Sr. No. | Mass | Distance from O |
| 1 | m1 = 1 kg | r1 = √2 /2 m |
| 2 | m2 = 2 kg | r2= √2 /2 m |
| 3 | m3 = 3 kg | r3= √2 /2 m |
| 4 | m4 = 4kg | r4 = √2 /2 m |
IO = ∑ miri² = m1r1² + m2r2² + m3r3² + m4r4²
∴ IO = (1)(√2 /2)² + (2)(√2 /2)² + (3)(√2 /2)² + (4)(√2 /2)²
∴ IO = (1)(0.5)² + 2(0.5)² + 3(0.5)² + 4(0.5)² = 10(0.5)² = 10 × 0.25 = 2.5 kg m²
M = m1 + m2 + m3 + m4 = 1 + 2 +3 + 4 = 10 kg
By definition of radius of gyration
IA = MKO²
∴ 2.5 = 10 KO²
∴ KO² = 0.25
∴ KO = 0.5 m
Ans: Moment of inertia of system about axis passing through O and perpendicular to the plane of ABCD is 2.5 kg m² and corresponding radius of gyration is 0.5 m.
Axis passing through Side AB:

| Sr. No. | Mass | Distance from AB |
| 1 | m1 = 1 kg | r1 = 0 m |
| 2 | m2 = 2 kg | r2= 0 m |
| 3 | m3 = 3 kg | r3= 1 m |
| 4 | m4 = 4kg | r4 = 1 m |
IAB = ∑ miri² = m1r1² + m2r2² + m3r3² + m4r4²
∴ IAB = (1)(0)² + (2)(0)² + (3)(1)² + (4)(1)²
∴ IAB = 0 + 0 + 3 + 4 = 7 kg m²
M = m1 + m2 + m3 + m4 = 1 + 2 +3 + 4 = 10 kg
By definition of radius of gyration
IAB = MKAB²
∴ 7 = 10 KAB²
∴ KAB² = 0.7
KAB = 0.837 m
Ans: Moment of inertia of system about side AB is 75 kg m² and corresponding radius of gyration is 0.837m.
Axis passing through Diagonal AC:

| Sr. No. | Mass | Distance from AC |
| 1 | m1 = 1 kg | r1 = 0 m |
| 2 | m2 = 2 kg | r2= √2 /2 m |
| 3 | m3 = 3 kg | r3= 0 m |
| 4 | m4 = 4kg | r4 = √2 /2 m |
IAC = ∑ miri² = m1r1² + m2r2² + m3r3² + m4r4²
∴ IAC = (1)(0)² + (2)(√2 /2)² + (3)(0)² + (4)(√2 /2)²
∴ IAC = 0 + (2)(0.5)² + 0 + 4(0.5)² = 7 kg m²
M = m1 + m2 + m3 + m4 = 1 + 2 +3 + 4 = 10 kg
By definition of radius of gyration
IAC = MKAC²
∴ 7 = 10 KAC²
∴ KAC² = 0.7
KAC = 0.837 m
Ans: Moment of inertia of system about diagonal AC is 75 kg m² and corresponding radius of gyration is 0.837m.
Example 02:
Three point masses 1 kg, 2 kg and 3 kg are located at the vertices A, B and C of an equilateral triangle ABC of side 1m. Find the moment of inertia and radius of gyration in each of the following cases when axis of rotation is
- passing through A and perpendicular to the plane of triangle ABC.
- passing through centroid G of the triangle and perpendicular to the plane of triangle ABC
- along the side AB
Given: m1 = 1 kg, m2 = 2 kg, m3 = 3 kg, AB = BC = AC = 1 m
Solution:
Axis passing through A and perpendicular to the plane of triangle ABC

| Sr. No. | Mass | Distance from A |
| 1 | m1 = 1 kg | r1 = 0 m |
| 2 | m2 = 2 kg | r2= 1 m |
| 3 | m3 = 3 kg | r3= 1m |
IA = ∑ miri² = m1r1² + m2r2² + m3r3²
∴ IA = (1)(0)² + (2)(1)² + (3)(1)²
∴ IA = 0 + 2 +3 = 5 kg m²
M = m1 + m2 + m3 = 1 + 2 +3 = 6 kg
By definition of radius of gyration
IA = MKA²
∴ 5 = 6 KA²
∴ KA² = 5/6 = 0.8333
KA = 0.913 m
Ans: Moment of inertia of system about A is 5 kg m² and corresponding radius of gyration is 0.913 m.
Passing through centroid G of the triangle and perpendicular to the plane of triangle ABC

For equilateral triangle GA = GB = GC = side/√3 = 1 / √3 = 0.577 m
| Sr.No. | Mass | Distance from A |
| 1 | m1 = 1 kg | r1 = 0.577 m |
| 2 | m2 = 2 kg | r2= 0.577 m |
| 3 | m3 = 3 kg | r3= 0.577 m |
IG = ∑ miri² = m1r1² + m2r2² + m3r3²
∴ IG = (1)(0.577)² + (2)(0.577)² + (3)(0.577)²
∴ IG = 1/3 + 2/3 +3/3 = 6/3 = 2 kg m²
M = m1 + m2 + m3 = 1 + 2 +3 = 6 kg
By definition of radius of gyration
IG = MKG²
∴ 2 = 6 KG²
∴ KG² = 2/6 = 0.3333
KG = 0.577 m
Ans: Moment of inertia of system about G is 2 kg m² and corresponding radius of gyration is 0.577 m.
Along the side AB

| Sr.No. | Mass | Distance from A |
| 1 | m1 = 1 kg | r1 = 0 m |
| 2 | m2 = 2 kg | r2= 0 m |
| 3 | m3 = 3 kg | r3= √3 /2=0.866 m |
IAB = ∑ miri² = m1r1² + m2r2² + m3r3²
∴ IAB = (1)(0)² + (2)(0)² + (3)(0.866)²
∴ IAB = 0 + 0 + 1.25 = 1.25 kg m²
M = m1 + m2 + m3 = 1 + 2 +3 = 6 kg
By definition of radius of gyration
IAB = MKAB²
∴ 1.25 = 6 KAB²
∴ KAB² = 1.25/6 = 0.2083
KAB = 0.456 m
Ans: Moment of inertia of system about G is 1.25 kg m² and corresponding radius of gyration is 0.456 m.
Example 03:
A light thin uniform rod of length 2 m has two bodies stuck to its ends. The mass of each body is 100 g. Find the moment of inertia of the system about a transverse axis passing through i) the centre of mass of the rod ii) one end of the rod.
Case – I: Axis through the centre of mass of the rod

| Mass (m) | Distance from axis of rotation (r) |
| m1 | r1 = l/2 = 2/2 = 1m |
| m2 | r2 = l/2 = 2/2 = 1m |

Case – II: Axis through the centre of mass of the rod

| Mass (m) | Distance from axis of rotation (r) |
| m1 | r1 = l = 2 m |
| m2 | r2 = 0 m |

Ans: The M.I. of the system about the axis passing through the centre is 0.2 kg m2 and about the axis passing through the end is 0.4 kg m2.
Next Topic: Kinetic Energy of Rotating Body