Science > Physics > Rotational Motion > Kinetic Energy of Rotating Body and Torque Acting on it
In this article, we shall study kinetic energy of rotating body and torque acting on it.
Kinetic Energy of a Rotating Body:
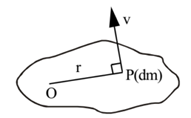
Consider a rigid body rotating about axis passing through point O and perpendicular to the plane of paper in anticlockwise sense as shown. Consider infinitesimal element at P of mass dm in the plane of the paper. Let distance of point P from the axis of rotation be r.
The moment of inertia of the rigid body is given by
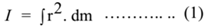
As the body is a rigid body, the element at P will start moving in a circular motion. Let v be its tangential or linear velocity.
Then by concepts of circular motion
v = r ω ……….. .. (2)
Due to this velocity, the element at P will possess kinetic energy which is given by

From equation (2) and (3)

Similarly, we can find the kinetic energy of each and every infinitesimal element in the body. The total kinetic energy of the body can be found by integrating both sides of the above equation.

This is an expression for the kinetic energy of a rotating body about a given axis.
Relation between kinetic energy of a rotating body and the frequency of its rotation
Substituting ω = 2πn in equation (5) we get

The quantities in the bracket are constant.
∴ E α n²
Thus, the kinetic energy of the rotating body about a given axis is directly proportional to the square of the frequency of the body.
Relation between kinetic energy of rotating a body and its angular momentum
The kinetic energy of the rotating body about a given axis is given by

Torque Acting on Rotating Body:
Consider a rigid body rotating about an axis passing through point O and perpendicular to the plane of the paper in an anticlockwise sense as shown. Let us consider the infinitesimal element at P of mass dm in the plane of the paper. Let the distance of this element from the axis of rotation be r.

The moment of inertia of the rigid body is given by

Let τ be the external torque acting on the body. Under the influence of this torque let the body rotates with angular acceleration α. Let dF be the magnitude of an external force acting on the element, in the plane of the page and at right angles to position vector of point P, then by Newton’s Second Law of motion,
dF = dm . a ……….. (2)
where ‘a’ is the magnitude of linear acceleration (tangential acceleration) of the element.
By the concept of circular motion, we know that
a = r α …………. (3)
From Equations (2) and (3)
dF = dm . r. α ……… (4)
Let dτ be the torque acting on the element, the magnitude of the torque is given by
dτ = r , dF ……………… (5)
From equations (4) and (5)
dτ = r , dm . r. α
dτ = r ² dm α
Similarly, we can find torque on each and every infinitesimal element in the body. The total torque acting on the body can be found by integrating both sides of the above equation

As the body is rigid body angular acceleration (α) of all the elements is the same and it is taken out of integration sign
From equations (1) and (6)
τ = Iα
This is an expression for torque acting on a rotating body.
Numerical Problems:
Example 01:
A disc of mass 50 Kg and radius 0.4 m is capable of rotation about an axis passing through its centre and at right angles to its plane. If a constant torque of 12 Nm acts on it, find the angular acceleration caused in the disc.
Given: Mass of disc = M = 50 kg, radius of disc = R = 0.4 m, Torque = τ = 12 Nm
To Find: Angular acceleration = α =?
Solution:
The M.I. of a disc about an axis passing through its centre and at right angles to its plane is given by
I = ½MR² = ½ × 50 × 0.4² = 25 × 0.16 = 4 kg m²
We have torque, τ = I α
∴ α = τ / I = 12/4 = 3 rad/s²
Ans: Angular acceleration = 3 rad/s²
Example 02:
A constant couple of 25 Nm acts on a flywheel of mass 100 kg and radius of gyration 25 cm. What is the resulting angular acceleration?
Given: Mass of flywheel (disc) = M = 100 kg, radius of gyration = K = 25 cm = 0.25 m, Torque = τ = 25 Nm
To Find: Angular acceleration = α =?
Solution:
The M.I. of a body in terms of the radius of gyration is given by
I = MK² = 100 × 0.25² = 100 × 0.0625 = 6.25 kg m²
We have torque, τ = I α
∴ α = τ / I = 25/6.25 = 4 rad/s²
Ans: Angular acceleration = 4 rad/s²
Example 03:
A constant torque of magnitude 5000 Nm acting on a body increases its angular velocity from 4 rad/s to 20 rad/s in 8 s. Calculate the M.I. of the body about the axis of rotation.
Given: Initial angular speed = ω1 = 4 rad/s, Final angular speed = ω2 = 20 rad/s, Time taken = t = 8 s, Torque = τ = 5000 Nm
To Find: Moment of Inertia = I = ?
Solution:
α = (ω2 – ω1)/t = (20- 4)/8 = 2 rad/s²
We have torque, τ = I α
∴ I = τ/ α = 5000/2 = 2500 kg m²
Ans: Moment of inertia of the body is 2500 kg m²
Example 04:
The speed of rotation of the body increases from 60 rpm to 90 rpm in 1 minute. Calculate the torque acting on the body if its M.I. is 500 kgm².
Given: Initial angular speed = N1 = 60 r.pm. Final angular speed = N2 = 90 r.pm., Time taken = t = 1 min = 60 s, Moment of Inertia = I = kgm²
To Find: Torque = τ =?
Solution:

We have torque, τ = I α
∴ τ = 500 × 0.0524 = 26.18 Nm
Ans: Torque acting is 26.18 Nm
Example 05:
A solid sphere of radius 25 cm and mass 25 kg rotates about a fixed axis passing through its centre. If its angular velocity changes from 2π rad/s to 12π rad/s in 5 s, calculate the torque applied.
Given: Radius of sphere = R = 25 cm = 0.25 m, Mass of sphere = 25 kg, Initial angular speed = ω1 = 2π rad/s, Final angular speed = ω2 = 12π rad/s, Time taken = t = 5 s,
To Find: Torque = τ =?
Solution:
M.I. of a sphere about a fixed axis passing through its centre is given by

α = (ω2 – ω1)/t = (12π- 2π)/5 = 2π = 2 × 3.142 = 6.284 rad/s²
We have torque, τ = I α
∴ τ = 0.625 × 6.284 = 3.928 Nm
Ans: Torque required is 3.928 Nm
Example 06:
The angular velocity of a disc rotating in its plane changes from 2 rad/s to 10 rad/s in one minute when a constant torque of 2 Nm applied. What is the M. I. of the disc?
Given: Initial angular speed = ω1 = 2 rad/s, Final angular speed = ω2 = 10 rad/s, Time taken = t = 1 min = 60 s, Torque = τ = 2 Nm
To Find: Moment of inertia of the disc = I =?
Solution:
α = (ω2 – ω1)/t = (10- 2)/60 = 8/60 = 0.1333 rad/s²
We have torque, τ = I α
∴ I = τ / α = 2/0.1333 = 15 kg m²
Ans: Moment of inertia of the disc is 15 kg m²
Example 07:
A flywheel in the form of a disc is initially at rest. When a constant torque acts upon it for one minute, it attains a speed of 300 r.p.m. Calculate the torque if the mass and radius of the disc are 10 kg and 0.4 m respectively.
Given: Radius of disc = R = 0.4 m Mass of disc = 10 kg, Initial angular speed = N1 = 0 rad/s, Final angular speed = N2 = 300 r.p.m., Time taken = t = 1 min = 60 s,
To Find: Torque = τ =?
Solution:
M.I. of disc about an axis passing through its centre and perpendicular to plane is given by
I = ½MR² = ½ × 10×0.4² = 0.8 kg m²
ω2 = 2πN2/ 60 = (2× π × 300)/60 = 10π rad/s
α = (ω2 – ω1)/t = (10π- 0)/60 = π/6 = 0.5237 rad/s²
We have torque, τ = I α
∴ τ = 0.8 × 0.5237 = 0.419 Nm
Ans: Torque required is 0.419 Nm
Previous Topic: Concept of Moment of Inertia
Next Topic: Principles of Parallel Axes and Perpendicular Axes