Science > Physics > Electrostatics > Capacitors in Series and Capacitors in Parallel
In this article, we shall study two simple capacitors circuits: capacitors in series and capacitors in parallel. We shall derive an expression for equivalent of such combination.
Equivalent Capacity of Condensers in Series:
A number of condensers are said to be joined in series if they are joined end to end and each condenser acquires the same charge. In series combination, the plates of each condenser carry a charge of the same magnitude. However, the potential difference across the whole combination is the sum of the potential difference across individual condensers.

Consider three condensers of capacities C1, C2 and C3 respectively, then the total potential drop is given by :
V = V1 + V2 + V3 ….(1)
This is the terminal p.d. of the cell. In series combination, the charge on each condenser is the same i.e. Q.
For the 1st condenser C1= Q/V1 Hence V1 = Q/C1
For the 2nd condenser, C2= Q/V2 Hence V2 = Q/C2
For the 3rd condenser, C3= Q/V3 Hence V3 = Q/C3
Substituting these values in equation (1)
V = Q/C1 + Q/C2 + Q/C3
∴ V = Q(1/C1 + 1/C2 + 1/C3) …………….. (2)
If the three condenses are replaced by an equivalent condenser of capacity ‘C’, then for equivalent or effective capacity of the condenser.
C = Q/V hence V = Q/C
Substituting in (2), we get,
Q/C = Q(1/C1 + 1/C2 + 1/C3)
∴ 1/C = 1/C1 + 1/C2 + 1/C3
In general, when ‘n’ condenser of capacity C1, C2, C3,…., Cn are connected in series, then their equivalent capacity is given by
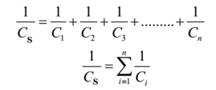
Thus when a number of condensers are connected in series the reciprocal of their resultant capacity is the sum of reciprocals of their individual capacities.
The resultant capacity of series combination is always less than the least capacity in the combination.
Equivalent Capacity of Condensers in Parallel:
A number of condensers are said to be joined in parallel if they are connected between two common points so that the potential difference across each condenser is the same. However, each condenser acquires a charge depending on its capacity.

Let us consider three condensers of capacity C1, C2 and C3 connected in parallel across a cell of terminal potential difference V. One plate of each condenser is connected to the positive terminal of the cell and the other plate is connected to the negative terminal. The total charge + Q supplied by the cell gets distributed over the condensers.
If Q1, Q2 and Q3 are the amounts of charge accumulated by condenser C1, C2 and C3 respectively, then charge supplied by the cell is given by
Q = Q1 + Q2 + Q3 ……….. (1)
In parallel combination p. d. across each condenser is the same i.e. This is also the terminal p. d. of the cell.
For the 1st condenser C1= Q1/VHence Q1 = C1V
For the 2nd condenser, C2= Q2/VHence Q2 = C2V
For the 3rd condenser, C3= Q3/VHence Q3 = C3V
Substituting these values in equation (1)
Q = C1V + C2V + C3V
∴ Q = V(C1 + C2 + C3) ……….. (2)
If the three condensers are replaced by an equivalent condenser of capacity C, then for equivalent or effective condenser,
C = Q/V hence Q = CV
Substituting in (2), we get,
CV = V(C1 + C2 + C3)
C = C1 + C2 + C3
In general, when ‘n’ condenser of capacities C1, C2, C3, …… Cn are connected in series, then their equivalent capacity is given by

Thus when a number of condensers are joined in parallel, their effective capacity equals the sum of the capacities of the individual condensers.
The resultant capacity of the parallel combination is always greater than the greatest capacity in the combination.
Previous Topic: Concept of the Capacity of a Conductor
Next Topic: Van De Graff Generator