Science > Physics > Oscillations: Simple Harmonic Motion > Theory of Simple Pendulum
In this article, we shall study a concept of a simple pendulum, its characteristics. We shall also derive an expression for the period of a simple pendulum.
A simple pendulum consists of a point mass suspended from a perfectly rigid support by a weightless, inextensible, twist less and perfectly flexible fibre. A heavy metal sphere having very very less radius than the length of the fibre can be treated as a point mass. This metal sphere is called as the bob of the simple pendulum. The distance between the point of suspension up to the centre of gravity of the bob is called as the length of the Simple pendulum.
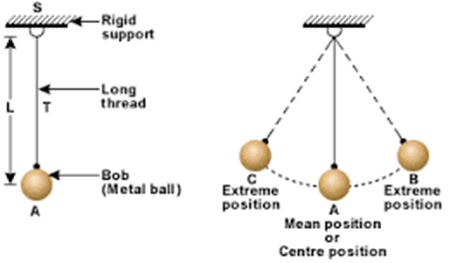
When the simple pendulum is in the equilibrium position, the centre of gravity of bob lies vertically below the point of suspension. Hence position SA is the equilibrium position. Let the bob be displaced slightly (angular displacement less than 5° to one side and then released. The bob starts oscillating to and from about its equilibrium or the mean position. We can prove that this motion of the bob is linear S.H.M.
Let ‘l’ be the length of the simple pendulum and ‘m’ be the mass of bob of the simple pendulum. Let us consider bob at some arbitrary position B on its path. Let the displacement AB be equal to x. Let q be the corresponding angular displacement, i.e. m ∠ BOA = θ.
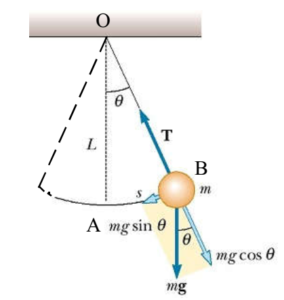
When the bob is at position B it is acted upon by following forces. The weight mg acting vertically downwards and the tension T’ in the string. The weight mg can be resolved into two components. mg sinθ along the path of oscillation of bob and towards the mean position and mg cosθ along OB
As the string is inextensible, the component mg cos θ must be balanced by tension in the string.
T = mg Cosθ
The component mg sin θ is directed towards the mean or equilibrium position and remains unbalanced. Therefore it acts as restoring force.
F = – mg Sinθ
The negative sign indicated that the force is opposite to the angular displacement
As angular displacement θ is very small
sin θ ≈ θ [θ measured in radian ]
F = – m g θ … (1)
From figure and geometry of a circle

For particular place acceleration due to gravity ‘g’ is constant. Mass of bob of the pendulum is constant. As the string is inextensible, the length of the simple pendulum ‘’ is constant. Hence quantity in the bracket is constant.
F ∝ -x
The above relation indicates that the force acting on the bob of the simple pendulum is directly proportional to the linear displacement which is defining a characteristic of simple harmonic motion. Hence the motion of the simple pendulum is linear S.H.M. for small amplitudes.
Period of Oscillation of Simple Pendulum:
Time taken by simple pendulum to complete one oscillation is called a Time period of the simple pendulum.
Force constant (k) is defined as restoring force per unit displacement.

This is an expression for the time period of oscillation of S.H.M.
Laws of a Simple Pendulum:
The period of a simple pendulum is given by

Where l = Length of a simple pendulum, g = acceleration due to gravity
From the above expression, we can have the following conclusions.
- Law of Mass: As the expression doesn’t contain the term ‘m’, the time period of the simple pendulum is independent of the mass and material of the bob. This property is known as the law of mass.
- Law of Length: The time period of the simple pendulum is directly proportional to the square root of its length. This property is known as the law of length.
- Law of Iscochronism: The time period of the simple pendulum is independent of the amplitude, provided the amplitude is sufficiently small. This property is known as the law of isochronism. The oscillation of the simple pendulum is isochronous.
- Law of gravity: The time period of a simple pendulum is inversely proportional to the square root of the acceleration due to gravity at that place. This property is known as the law of acceleration due to gravity.
The above conclusions are sometimes referred as laws of a simple pendulum.
The Frequency of Oscillation of a Simple Pendulum:
The period of a simple pendulum is given by

Where l = Length of a simple pendulum, g = acceleration due to gravity
Now the frequency is related to period as n = 1 /T

Seconds Pendulum:
A simple pendulum whose time period is two seconds is called seconds pendulum. We know that

Squaring both sides we get

Thus the length of seconds pendulum is 0.99 m (approx. 1m)
Previous Topic: Composition of Two S.H.M.s
Next Topic: Numerical Problems on Simple Pendulum