Science > Physics > Units and Measurement > Measurement of Length, Area, and Volume > Measurement of Area and Volume
In this article, we shall study methods of the measurement of area and volume.
Measurement of Area:
Measurement of Area of Irregular Shape:
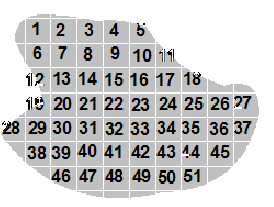
The area of an irregular object can be obtained by drawing an outline of the shape of the object on a graph paper of 1 square centimeter marked square.
- The number of complete squares is counted.
- Next squares more than half are also counted as a complete square.
- Squares less than half are left and not counted.
- The sum of all the squares counted gives the area of the shape in square centimetres.
- In the above figure, the area of the shape is 51 square units.
Measurement of Area of Regular Shapes:
- Area of a triangle = 1/2 x base x height
- Area of a square = side²
- Area of a rectangle – length x breadth
- Area of a circle = π(radius)² = π/4 x (diameter)²
- Area of a parallelogram = base x height
- Area of a rhombus = 1/2 x product of diagonals
- Area of trapezium = 1/2 x sum of parallel sides x Distance between parallel lines
Units of Area:
S.I. unit of area is m² and read as a square metre. c.g.s unit of area is cm² and read as square centimeters. Land areas are bigger hence the area of land is measured in a hectare. 1 hectare = 10000 m²
Numerical Problems:
Example – 01:
An artist designed two postage stamps. One was square and measured 2 cm X 2 cm. The other was rectangular and measured 3 cm X 2 cm. Before the stamp was issued, it was decided to double the length of each side of a square stamp and triple the length of each side of a rectangular stamp. By how many times will the area of the paper required for each stamp increase.
Solution:
Square Stamp:
Initial area of square stamp = 2 cm x 2 cm = 4 cm².
New area of square stamp = (2 x 2) cm x (2 x 2) cm = 16 cm².
The area of the paper for square stamp will increase by (16 cm²/4 cm²) 2 times
Rectangular Stamp:
Initial area of rectangular stamp = 2 cm x 3 cm = 6 cm².
New area of rectangular stamp = (3 x 2) cm (3 x 3) cm = 54 cm².
The area of the paper for rectangular stamp will increase by (54 cm²./6 cm²) 9 times
Example – 02:
The length of a school compound is 500 m and the breadth is 120 m. Find the area of the school in hectares.
Solution:
Area = Length x Breadth = 500 x 120 = 60000 m²
Now 1 hectare = 10000 m²
The area of school = (60000 m² / 60000 m²) = 6 hectares,
Measurement of Volume:
Volume is the space occupied by an object. The S.I. unit of volume is m³. Its c.g.s. unit is c.c. i.e cm³. Other practical units are millilitre (ml), litre (l) etc. The volume of regular bodies can be obtained by measuring the necessary dimensions for the calculation of the volume.
Measurement of Volume of Regular Solids:
- Volume of rectangular parallelepiped = length x breadth x height
- Volume of cube = side³.
- Volume of cylinder = πr²h
- Volume of cone = 1/3 x πr²h
Volume of Liquids:
Measurement of volume of a liquid is done using the following apparatus
Measuring Jar:
It is a graduated glass jar marked in ml from bottom to top. It is used to measure required amount of liquid.

Measuring Flask:
It has one mark etched at the neck and the liquid of the only volume of its capacity can be measured.

Pipette:
It is filled by sucking the liquid into it. It is used to take a fixed amount of liquid.

Burette:
It is a tube similar to measuring jar, with a pitch cock provided at the bottom. It is used to take the desired amount of liquid.

Precaution: Read from the bottom of the curved surface of the liquid called meniscus.
Measurement of volume using Measuring jar by the direct method:
Pour the liquid in the measuring jar carefully and fill the jar with liquid as per the required quantity by reading the meniscus of the liquid in the measuring jar.
Measurement of Volume of Irregular Solids:
Solid Insoluble in Water but Heavier Than Water:

- Take some water in the measuring jar. Note the volume V1 cm³ of this water.
- Immerse the solid carefully and completely in water.
- Note the volume V2 cm³ of water with solid in it.
- Calculate increase in volume = V2 – V1
- Then volume of solid = (V2 – V1) cm³.
Solid Insoluble in Water but Lighter Than Water:
- For this sinker (heavy body) has to be used.
- Take some water in the measuring jar. Note the volume V1 cm³ of this water when the sinker is in water.
- Tie sinker to the solid and immerse the solid with the sinker carefully and completely in water.
- Note the volume V2 cm³ of water with solid and sinker in it.
- Calculate increase in volume = V2 – V1
- Then volume of solid = (V2 – V1) cm³.
Note: For solids soluble in water a liquid other than water, in which the solid is insoluble is used.
To Find Average Volume of a Single Drop of water:
- Take clean burette with water. Clamp it upright. Remove any air bubbles formed.
- Now allow the water to trickle slowly drop by drop in measuring jar.
- Count the number of drops collected in the measuring jar.
- Measure the volume of water in the measuring jar and use the following formula to find the volume of a drop of water.
- Volume drop = Volume of water collected / No. of drops
To Find Average Volume of Lead Shot:
- Take some water in the measuring jar. Note the volume V1 cm³ of this water.
- Drop ‘n’ numbers of lead shot in the measuring jar carefully.
- Note the volume V2 cm³ of water with lead shots in it.
- Calculate the increase in volume = V2 – V1
- The volume of each drop = Increase in volume / No. of lead shots (n)
Numerical Problems:
Example – 03:
A stone X is immersed in water taken in a measuring jar. The water level rises from 60 cm³ to 78 cm³. If a second stone Y is immersed in water, the level rises from 60 cm³ to 86 cm³. What is the rise in the level of water when stone X and Y are immersed simultaneously? What is reading in the measuring jar?
Solution:
Volume of stone X = 78 cm³ – 60 cm³ = 18 cm³.
Volume of stone Y = 86 cm³ – 60 cm³ = 26 cm³.
Total Volume of stone X and stone Y = 18 cm³ + 26 cm³ = 44 cm³.
Rise in the level of water in measuring flask = 44 cm³.
The level of water in the measuring jar after immersing both the stones = 60 cm³ + 44 cm³ = 104 cm³.
Rise in the level of water in measuring flask = 44 cm³ and Reading of measuring jar = 104 cm³
Example – 04:
Two identical lead balls are immersed into a measuring jar containing water, the level of water raises from 16 cm³ to 26 cm³. If one of the above lead ball and another metallic ball are immersed simultaneously, then the level of water in measuring jar raises from 20 cm³ to 40 cm³. Find the volume of the lead ball and metallic ball.
Solution:
Volume of two lead balls = 26 cm³ – 16 cm³ = 10 cm³.
Thus, volume of each lead ball = 10 cm³/2 = 5 cm³.
Volume of one lead ball + Volume of metallic ball = 40 cm³ – 20 cm³ = 20 cm³.
Volume of metallic ball = 20 cm³ – Volume of one lead ball = 20 cm³ – 5 cm³ = 15 cm³
Hence the volume of lead ball is 5 cm3 and that of metallic ball is 15 cm³.
Example – 05:
When 20 drops of water are allowed to collect in a measuring jar containing water, the level of water raises from 26 cm³ to 28 cm³. Find the average volume of each drop.
Solution:
Volume of 20 water drops = 28 cm³ – 26 cm³ = 2 cm³.
Volume of each drop = Volume of 20 water drops / 20 = 2 cm³ / 20 = 0.1 cm³
For More Topics in Measurement of Length, Area, and Volume Click Here
2 replies on “Measurement of Area and Volume”
good
Nice one