Management > Managerial Statistics > Index Number By Larpeyre’s Method
When all commodities are not of equal importance, we assign a weight to each commodity relative to its importance and the index number computed from these weights is called a weighted index number. For example, when calculating the price index number if the price of a unit of rice is twice the price of a unit sugar then the rice will be weighed in as ‘2’ whereas sugar will be weighed in as ‘1’. Hence it is a relatively average measure. It is more realistic in comparison to simple index number because it accurately reflects the change over time. Example of the weighted index number is that obtained by Laspeyre’s method, or by Paasche’s method, or by Fisher method.
If ‘w’ is the weight attached to a commodity, then price index is given by
P01 = (∑ P1 x w) / ( ∑ P0 x w) × 100
Example – 01:
Compute the weighted price index from the following data .
|
Commodity |
1995 |
2000 |
Weights |
|
A |
0.50 |
0.75 |
2 |
|
B |
0.60 |
0.75 |
5 |
|
C |
2.00 |
2.40 |
4 |
|
D |
1.80 |
2.10 |
8 |
|
E |
8.00 |
10.00 |
1 |
Solutions:
|
Commodity |
1995 |
2000 |
Weights |
P0w |
P1w |
|
A |
0.50 |
0.75 |
2 |
1 |
1.5 |
|
B |
0.60 |
0.75 |
5 |
3 |
3.75 |
|
C |
2.00 |
2.40 |
4 |
8 |
9.6 |
|
D |
1.80 |
2.10 |
8 |
14.4 |
16.8 |
|
E |
8.00 |
10.00 |
1 |
8 |
10 |
|
Total |
34.4 |
41.65 |
P01 = (∑ P1 x w) / ( ∑ P0 x w) × 100
P01 = (41.65 / 34.4) × 100
P01 = 121.07
Hence the weighted price index is 121.07
Different Weighted Index Methods:
- Laspeyre’s Method
- Paasche’s Method
- Dorbish and Browley’s Method
- Fisher’s Ideal Index Method
Price Index by Laspeyre’s Method:
Laspeyre’s method is based on fixed weights of the base year. For price index base year’s quantities are used as weights.
Steps involved:
- Denote prices of the commodity in the current year as P1.
- Denote prices of the commodity in the base year as P0 and its quantity consumed in that year by Q0.
- Find the quantities P0Q0 and P1Q0 for each commodity.
- Find the sum of each column of P0Q0 and P1Q0 and denote the sums by ∑ P0Q0 and ∑ P1Q0 respectively.
- Use the following formula to find the Price index number
LP01 = (∑ P1 x Q0) / ( ∑ P0 x Q0) × 100
Example – 02:
Compute Price index by Laspeyre’s Method from the following data.
|
Commodity |
Base Year |
Current Year |
||
|
Price |
Quantity |
Price |
Quantity |
|
|
A |
3 |
25 |
5 |
28 |
|
B |
1 |
50 |
3 |
60 |
|
C |
2 |
30 |
1 |
30 |
|
D |
5 |
15 |
6 |
12 |
Solution:
|
Commodity |
Base Year |
Current Year |
||||
|
Price (P0) |
Quantity (Q0) |
Price (P1) |
Quantity(Q1) |
P0Q0 |
P1Q0 |
|
|
A |
3 |
25 |
5 |
28 |
75 |
125 |
|
B |
1 |
50 |
3 |
60 |
50 |
150 |
|
C |
2 |
30 |
1 |
30 |
60 |
30 |
|
D |
5 |
15 |
6 |
12 |
75 |
90 |
|
Total |
∑P0Q0=260 |
∑P1Q0=395 |
||||
LP01 = (∑ P1 x Q0) / (∑ P0 x Q0) × 100
LP01 = (395 / 260) × 100
LP01 = 151.92
Thus Laspeyre’s price index number is 151.92
Quantity Index by Laspeyre’s Method
Laspeyre’s method is based on fixed weights of the base year. For quantity index base year’s prices are used as weights.
Steps involved:
- Denote prices of the commodity in the current year as P1 and its quantity consumed in that year by Q1.
- Denote prices of the commodity in the base year as P0.
- Find the quantities Q0P0 and Q1P0 for each commodity.
- Find the sum of each column of Q0P0 and Q1P0 and denote the sums by ∑ Q0P0 and ∑ Q1P0 respectively.
- Use following formula to find the Price index number
LQ01 = (∑ Q1 x P0) / ( ∑ Q0 x P0) × 100
Example – 03:
Compute Quantity index by Laspeyre’s Method from the following data.
|
Commodity |
Base Year |
Current Year |
||
|
Price |
Quantity |
Price |
Quantity |
|
|
A |
3 |
25 |
5 |
28 |
|
B |
1 |
50 |
3 |
60 |
|
C |
2 |
30 |
1 |
30 |
|
D |
5 |
15 |
6 |
12 |
Solution:
|
Commodity |
Base Year |
Current Year |
||||
|
Price (P0) |
Quantity (Q0) |
Price (P1) |
Quantity(Q1) |
Q0P0 |
Q1P0 |
|
|
A |
3 |
25 |
5 |
28 |
75 |
84 |
|
B |
1 |
50 |
3 |
60 |
50 |
60 |
|
C |
2 |
30 |
1 |
30 |
60 |
60 |
|
D |
5 |
15 |
6 |
12 |
75 |
60 |
|
Total |
∑Q0P0=260 |
∑Q1P0=264 |
||||
LQ01 = (∑ Q1 x P0) / (∑ Q0 x P0) × 100
LQ01 = (264 / 260) × 100
LQ01 = 101.54
Thus Laspeyre’s quantity index number is 101.54
Example – 04:
Compute Price index and Quantity index by Laspeyre’s Method from the following data.
|
Commodity |
Base Year 1997 |
Current Year 2005 |
||
|
Price |
Quantity |
Price |
Quantity |
|
|
A |
16 |
110 |
25 |
132 |
|
B |
5 |
220 |
5 |
264 |
|
C |
10 |
132 |
15 |
165 |
|
D |
25 |
66 |
30 |
55 |
Solution:
|
Commodity |
Base Year |
Current Year |
|||||
|
(P0) |
(Q0) |
(P1) |
(Q1) |
Q0P0 |
Q0P1 |
Q1P0 |
|
|
A |
16 |
110 |
25 |
132 |
1760 |
2750 |
2112 |
|
B |
5 |
220 |
5 |
264 |
1100 |
1100 |
1320 |
|
C |
10 |
132 |
15 |
165 |
1320 |
1980 |
1650 |
|
D |
25 |
66 |
30 |
55 |
1650 |
1980 |
1375 |
|
Total |
5830 |
7810 |
6457 |
||||
Price Index:
LP01 = (∑ P1 x Q0) / (∑ P0 x Q0) × 100
LP01 = (7810 / 5830) × 100
LP01 = 133.96
Thus Laspeyre’s price index number is 133.96
Quantity Index:
LQ01 = (∑ Q1 x P0) / (∑ Q0 x P0) × 100
LQ01 = (6457 / 5830) × 100
LQ01 = 110.75
Thus Laspeyre’s quantity index number is 110.75
Merits of Laspeyre’s Method :
- Weights (the quantities) are only needed for one year, the base year.
- Due to above reason this it is cheaper to construct.
- It is easy to calculate and commonly used.
- Quantities for future years do not need to be calculated – only base year quantities (weightings) are used
- The indexes for each year can be compared directly. It provides A meaningful comparison as changes in the index are attributed to the changes.
Demerits of Laspeyre’s Method :
- More expensive new goods that cause an upward bias in prices.
- Does not take account of changes in demand.
- Substituting goods or services that have become relatively cheaper for those that have become relatively more expensive.
- Price increases solely due to quality improvements. It should not be considered inflation.
Previous Topic: Simple Average of Relative Method
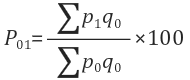
2 replies on “Lapeyre’s Index Number”
Very understandable
Thanks for such simplified way of braking this topic ,I appreciate the review and method.