Management > Managerial Statistics > Index Number By Paasche’s Method
Price Index Number by Paasche’s Method:
Paasche’s method is based on fixed weights of the current year. For price index current year’s quantities are used as weights.
Steps involved:
- Denote prices of the commodity in the current year as P1 and its quantity consumed in that year by Q1.
- Denote prices of the commodity in the base year as P0.
- Find the quantities P0Q1 and P1Q1 for each commodity.
- Find the sum of each column of P0Q1 and P1Q1 and denote the sums by ∑ P0Q1 and ∑ P1Q1 respectively.
- Use the following formula to find the Price index number
PP01 = (∑ P1 x Q1) / ( ∑ P0 x Q1 ) × 100
Example – 01:
Compute Price index by Paasche’s Method from the following data .
|
Commodity |
Base Year |
Current Year |
||
|
Price |
Quantity |
Price |
Quantity |
|
|
A |
3 |
25 |
5 |
28 |
|
B |
1 |
50 |
3 |
60 |
|
C |
2 |
30 |
1 |
30 |
|
D |
5 |
15 |
6 |
12 |
Solution:
|
Commodity |
Base Year |
Current Year |
||||
|
Price (P0) |
Quantity (Q0) |
Price (P1) |
Quantity(Q1) |
P0Q1 |
P1Q1 |
|
|
A |
3 |
25 |
5 |
28 |
84 |
140 |
|
B |
1 |
50 |
3 |
60 |
60 |
180 |
|
C |
2 |
30 |
1 |
30 |
60 |
30 |
|
D |
5 |
15 |
6 |
12 |
60 |
72 |
|
Total |
∑P0Q1=264 |
∑P1Q1=422 |
||||
PP01 = (∑ P1 x Q1) / (∑ P0 x Q1) × 100
PP01 = (422 / 264) × 100
PP01 = 159.85
Thus Paasche’s price index number is 159.85
Quantity Index by Paasche’s Method
Paasche’s method is based on fixed weights of the current year. For quantity index, current year’s prices are used as weights.
Steps involved:
- Denote prices of the commodity in the current year as P1 and its quantity consumed in that year by Q1.
- Denote prices of the commodity in the base year as P0 and its quantity consumed in that year by Q0.
- Find the quantities Q0P1 and Q1P1 for each commodity.
- Find the sum of each column of Q0P1 and Q1P1 and denote the sums by ∑ Q0P1 and ∑ Q1P1 respectively.
- Use the following formula to find the Quantity index number
PQ01 = (∑ Q1 x P1) / ( ∑ Q0 x P1) × 100
Example – 02:
Compute Quantity index by Laspeyre’s Method from the following data by Laspeyre’s method .
|
Commodity |
Base Year |
Current Year |
||
|
Price |
Quantity |
Price |
Quantity |
|
|
A |
3 |
25 |
5 |
28 |
|
B |
1 |
50 |
3 |
60 |
|
C |
2 |
30 |
1 |
30 |
|
D |
5 |
15 |
6 |
12 |
Solution:
|
Commodity |
Base Year |
Current Year |
||||
|
Price (P0) |
Quantity (Q0) |
Price (P1) |
Quantity(Q1) |
Q0P1 |
Q1P1 |
|
|
A |
3 |
25 |
5 |
28 |
125 |
140 |
|
B |
1 |
50 |
3 |
60 |
150 |
180 |
|
C |
2 |
30 |
1 |
30 |
30 |
30 |
|
D |
5 |
15 |
6 |
12 |
90 |
72 |
|
Total |
∑Q0P1=395 |
∑Q1P1=422 |
||||
PQ01 = (∑ Q1 x P1) / ( ∑ Q0 x P1) × 100
PQ01 = (422 / 395) × 100
PQ01 = 106.84
Thus Paasche’s quantity index number is 106.84
Example – 03:
Compute Price index and Quantity index by Paasche’s Method from the following data.
|
Commodity |
Base Year 1997 |
Current Year 2005 |
||
|
Price |
Quantity |
Price |
Quantity |
|
|
A |
16 |
110 |
25 |
132 |
|
B |
5 |
220 |
5 |
264 |
|
C |
10 |
132 |
15 |
165 |
|
D |
25 |
66 |
30 |
55 |
Solution:
|
Commodity |
Base Year |
Current Year |
|||||
|
(P0) |
(Q0) |
(P1) |
(Q1) |
Q1P1 |
Q0P1 |
Q1P0 |
|
|
A |
16 |
110 |
25 |
132 |
3300 |
2750 |
2112 |
|
B |
5 |
220 |
5 |
264 |
1320 |
1100 |
1320 |
|
C |
10 |
132 |
15 |
165 |
2475 |
1980 |
1650 |
|
D |
25 |
66 |
30 |
55 |
1650 |
1980 |
1375 |
|
Total |
8745 |
7810 |
6457 |
||||
Price Index:
PP01 = (∑ P1 x Q1) / (∑ P0 x Q1) × 100
PP01 = (8745 / 6457) × 100
PP01 = 135.43
Thus Paasche’s price index number is 135.43
Quantity Index:
PQ01 = (∑ Q1 x P1) / ( ∑ Q0 x P1) × 100
PQ01 = (8745 / 7810) × 100
PQ01 = 111.97
Thus Paasche’s quantity index number is 111.97
Merits of Paasche’s Method :
- Uses current quantities (weights) and so takes changes in consumption patterns into account.
- Does not overstate price increases.
Demerits of Paasche’s Method :
- Not a pure index as price and quantities change.
- Long and expensive to update weights.
- The indexes for each year cannot be compared directly since the quantities change
- Paasche index tends to underestimate the rise in prices or has a downward bias.
- Paasche index is not frequently used in practice when the number of commodities is large. This is because, for Paasche index, revised weights or quantities must be computed for each year examined. Such information is either unavailable or hard to gather. It makes the data gathering expensive.
Previous Topic: Laspeyre’s Method
Next Topic: Dorbish and Bowley’s method
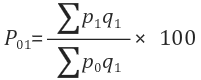
One reply on “Paasche’s Index Number”
Thank you for your elaborate statistics.am helped cos I had an activity to solve.
I request u to give relationship of qty and price index.
Formula for fishers ideal index