Index Number By Simple Aggregative Method

Management > Managerial Statistics > Index Number By Simple Aggregative Method

In Simple Aggregative Method, the total price of commodities in a given (current) year is divided by the total price of commodities in a base year and expressed as a percentage.

Steps involved in Simple Aggregative Method:

1. Add the prices of all the commodities in the current year. Denote the sum as ∑ P₁
2. Add the prices of all the commodities in the base year. Denote the sum as ∑ P_o
3. Use the following formula to find simple price index number of current year based on the base year.

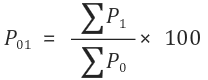
Problems Based on Fixed Base Year Method:

Example – 01:

Prices of commodities for the year 2000 and 2004 are as given in the table. Find the simple aggregative price index from the data displayed in the table.

Commodity	Unit	Price in Rs. Per unit
		2000	2004
Wheat	1 kg	10	15
Rice	1 kg	40	30
Pulses	1 kg	10	12
Onions	1 kg	5	13
Oil	1 litre	40	50

Solution:

Commodity	Unit	Price in Rs. Per unit
		2000	2004
Wheat	1 kg	10	15
Rice	1 kg	40	30
Pulses	1 kg	10	12
Onions	1 kg	5	13
Oil	1 litre	40	50
Total		∑P1 = 105	∑Po = 120

The price index number for 2004 taking 2000 as base year is given by

P₀₁ = (∑P₁ / ∑P₀) × 100

P₀₁ = (120 / 105) × 100

P₀₁ = 114.3

It indicates that the prices in the year 2004 had increased by 14.3 % as compared to the year 2000.

Example – 02:

Prices of commodities for the year 2000 and 2004 are as given in table. Find the simple aggregative price index from the data displayed in the table.

Commodity	Unit	Price in Rs. Per quintal
		2001	2002
Wheat	1 quintal	80	100
Rice	1 quintal	120	250
Grams	1 quintal	100	150
Pulses	1 quintal	200	300

Solution:

Commodity	Unit	Price in Rs. Per quintal
		2001	2002
Wheat	1 quintal	80	100
Rice	1 quintal	120	250
Grams	1 quintal	100	150
Pulses	1 quintal	200	300
Total		∑P1 = 500	∑Po = 800

The price index number for 2004 taking 2000 as base year is given by

P₀₁ = (∑P₁ / ∑P_o) × 100

P₀₁ = (800 / 500) × 100

P₀₁ = 160

It indicates that the prices in the year 2002 had increased by 60 % as compared to the year 2001.

Example – 03:

Prices of commodities for the year 2000, 2001, 2002, and 2003 are as given in table. Find the simple aggregative price index from the data displayed in the table taking 2000 as base year.

	Prices
Commodity	2000	2001	2002	2003
Wheat	23	23	24	26
Rice	24	40	56	72
Barley	25	28	28	29
Sugar	81	84	90	99

Solution:

	Prices
Commodity	2000	2001	2002	2003
Wheat	23	23	24	26
Rice	24	40	56	72
Barley	25	28	28	29
Sugar	81	84	90	99
Total	153	175	198	226

The price index number for 2001 taking 2000 as base year is given by

P₀₁ = (∑P₁ / ∑P_o) × 100

P_{2000, 2001} = (175 / 153) × 100

P_{2000, 2001} = 114.4

The price index number for 2002 taking 2000 as base year is given by

P₀₁ = (∑P₁ / ∑P_o) × 100

P_{2000, 2002} = (198 / 153) × 100

P_{2000, 2002} = 129.4

The price index number for 2003 taking 2000 as base year is given by

P₀₁ = (∑P₁ / ∑P_o) × 100

P_{2000, 2003} = (226 / 153) × 100

P_{2000, 2003} = 147.7

Problems Based on Chain Base Year Method:

Example – 04:

Prices of commodities for the year 2000, 2001, 2002, and 2003 are as given in table. Find the simple aggregative price index from the data displayed in the table using chain base method.

Solution:

	Prices
Commodity	2000	2001	2002	2003
Wheat	23	23	24	26
Rice	24	40	56	72
Barley	25	28	28	29
Sugar	81	84	90	99

Solution:

	Prices
Commodity	2000	2001	2002	2003
Wheat	23	23	24	26
Rice	24	40	56	72
Barley	25	28	28	29
Sugar	81	84	90	99
Total	153	175	198	226

The price index number for 2001 taking 2000 as base year is given by

P₀₁ = (∑P₁ / ∑P_o) × 100

P_{2000, 2001} = (175 / 153) × 100

P_{2000, 2001} = 114.4

The price index number for 2002 taking 2001 as base year is given by

P₀₁ = (∑P₁ / ∑P_o) × 100

P_{2001, 2002} = (198 / 175) × 100

P_{2001, 2002} = 113.1

The price index number for 2003 taking 2002 as base year is given by

P₀₁ = (∑P₁ / ∑P_o) × 100

P_{2002, 2003} = (226 / 198) × 100

P_{2002, 2003} = 114.1

Merits and Demerits of Simple Aggregative Method:

Merits of Simple Aggregative Method:

• This is the simplest method of constructing index number.
• It is very easy to understand.
• It is very simple calculate.

Demerits of Simple Aggregative Method:

• It is affected by the magnitude of the prices of the different commodities.
• It is influenced by the units of the articles through which the prices are quoted.
• It is based on the assumption that the various items and their prices are expressed in the same unit.
• It ignores the relative importance of the different commodities included in the index number as no consideration is given to the relative importance of the commodities.
• It is unduly affected by high and low values of the commodities selected.
• It is not capable of being calculated through other averages viz. geometric mean, median, etc.

Previous Topic: Construction of Index Number

Next Topic: Index Number by Simple Average of Relative Method

Management > Managerial Statistics > Index Number By Simple Aggregative Method