Simple Average of Relative Method

Management > Managerial Statistics > Index Number By Simple Average of Relative Method

Simple Average of Relative Method Using Arithmetic Mean:

In this method, average of price relative of commodity is calculated.

Steps involved

1. Find price relative for each commodity for the current year using the formula R = (P1 / P0) × 100.
2. Add all price relatives of all the commodities.
3. Divide sum obtained in step 2 by the number of commodities (N).
4. Overall formula for the method is.

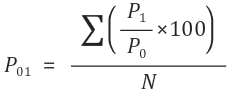
Example – 01:

Prices of commodities for the year 2000 and 2004 are as given in the table. Find the price index by a simple average of relative method and using the arithmetic mean from the data given in the table.

Commodity	Unit	Price in Rs. Per unit
		2000	2004
Wheat	1 kg	10	15
Rice	1 kg	40	30
Pulses	1 kg	10	12
Onions	1 kg	5	13
Oil	1 litre	40	50

Solution:

Commodity	Unit	Price in Rs. Per unit		R = (P1 / P0) × 100
		2000	2004
Wheat	1 kg	10	15	(15/10) x 100 = 150.0
Rice	1 kg	40	30	(30/40) x 100 = 75.0
Pulses	1 kg	10	12	(12/10) x 100 = 120.0
Onions	1 kg	5	13	(13/5) x 100 = 260.0
Oil	1 litre	40	50	(50/40) x 100 = 125.0
Total				∑ R = 730

The price index number by simple average of relative method  using arithmetic mean for 2004 taking 2000 as base year is given by

P₀₁ = (1/N)(∑ R)

P₀₁ = (1/5)(730)

P₀₁ = 146.0

Simple Average Relative Method Using Geometric Mean:

Steps involved

1. Find price relative for each commodity for the current year using the formula R = (P1 / P0) × 100.
2. Find log R in each case.
3. Add all logs of price relatives of all the commodities.
4. Divide sum obtained in step 3 by the number of commodities (N).
5. Find antilog of the number obtained in step 4
6. Overall formula for the method is.

P₀₁ =Antilog ((1/N) (∑ Log R)) = Antilog [(1/N)(∑ log ((P₁ / P₀) × 100)))]

Example – 02:

Prices of commodities for the year 2000 and 2004 are as given in table. Find the price index by simple average of relative method and using geometric mean from the data given in the table.

Commodity	Unit	Price in Rs. Per unit
		2000	2004
Wheat	1 kg	10	15
Rice	1 kg	40	30
Pulses	1 kg	10	12
Onions	1 kg	5	13
Oil	1 litre	40	50

Solution:

Commodity	Unit	Price in Rs. Per unit		R = (P1 / P0) × 100	Log R
		2000	2004
Wheat	1 kg	10	15	(15/10) x 100 = 150.0	Log 150 = 2.1761
Rice	1 kg	40	30	(30/40) x 100 = 75.0	Log 75 = 1.8751
Pulses	1 kg	10	12	(12/10) x 100 = 120.0	Log 120 = 2.0792
Onions	1 kg	5	13	(13/5) x 100 = 260.0	Log 260 = 2.4250
Oil	1 litre	40	50	(50/40) x 100 = 125.0	Log 125 = 2.0970
Total					∑ Log R = 10.6704

The price index number by simple average of relative method 

using geometric mean for 2004 taking 2000 as base year is given by

P₀₁ = Antilog [(1/N)(∑ log R)]

P₀₁ = Antilog [(1/5)(10.6704)]

P₀₁ = Antilog 2.1341

P₀₁ = 136.2

Example – 03:

Prices of commodities for the year 2002 and 2003 are as given in table. Find the price index by a simple average of relative method and using a) arithmetic mean and b) geometric mean.

	Prices
Commodity	2002	2003
Corn	800	880
Wheat	500	480
Cocoa	900	940

Solution:

	Prices		R = (P1 / P0) × 100	Log R
Commodity	2002	2003
Corn	800	880	(880/800) x 100 = 110	Log 110 = 2.0414
Wheat	500	480	(480/500) x 100 = 96	Log 96 = 1.9823
Cocoa	900	940	(940/900) x 100 = 104.44	Log 104.4 = 2.0187
Total			∑ R = 310.44	∑ log R = 6.0424

Solution:

Simple average of relative method and using arithmetic mean:

The price index number by simple average of relative method 

using arithmetic mean for 2003 taking 2002 as base year is given by

P₀₁ = (1/N)(∑ R)

P₀₁ = (1/3)(310.44)

P₀₁ = 103.48

Simple average of relative method and using geometric mean:

The price index number by simple average of relative method 

using geometric mean for 2003 taking 2002 as base year is given by

P₀₁ = Antilog [(1/N)(∑ log R)]

P₀₁ = Antilog [(1/3)( 6.0424)]

P₀₁ = Antilog 2.0141

P₀₁ = 103.30

Merits of Simple Average of Relative Method:

• It is not affected by units in which prices are quoted.
• As prices are converted into price relatives, it is not affected by absolute values of prices.
• It gives equal importance to all items and hence extreme values of certain items do not unduly affect the index number.
• The index number calculated by this method satisfies the unit test.

Demerits of Simple Average of Relative Method:

• As it is unweighted average, the importance of all the items is assumed to be the same.
• The index number constructed by this method does not satisfy the criteria laid down for index number.
• The index number is unduly influenced by high or low prices when the arithmetic mean is used.
• The index number constructed using geometric mean is tedious and time-consuming.

Previous Topic: Index Number by Simple Aggregative Method

Next Topic: Index Number by Laspeyre’s Method

Management > Managerial Statistics > Index Number By Simple Average of Relative Method