Tests for Adequacy of Index Number

Several formulae have been suggested for constructing index numbers and the problem is that of selecting the most appropriate one in a given situation. The different tests are the unit test, time reversal test, factor reversal test, and circular test.

Unit Test: 

This test states that the formula for constructing an index number should be independent of the units in which prices and quantities are expressed. All methods, except simple aggregative method, satisfy this test. Except for unweighted aggregative index number, all other indices satisfy this test.

Time Reversal Test:

This test guides whether the method works both ways in time forward and backward. According to Prof. Fisher, the formula for calculating an index number should be such that it gives the same ratio between one point of time and the other, no matter which of the two time is taken as the base. In other words, when the data for any two years are treated by the same method, but with the base reversed, the two index numbers should be reciprocals of each other.

Symbolically the test is represented as: P₀₁ X P₁₀ = 1

Where, P₀₁ is the index for time “1” on time “0” as base and P₁₀ is the index for time “0” on time “1” as the base. If the product is not unity, the method suffers from time bias. The multiplying factor 100 should not be considered during the test. Time reversal test is satisfied by

1. Simple aggregative method
2. Fisher’s method
3. Marshall Edgeworth’s method and
4. Kelly’s method.

Let us see how Fisher’s ideal method satisfies the test.

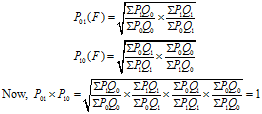
Thus Fisher’s method satisfies the time reversal test

Factor Reversal Test :

It says that the product of a price index and the quantity index should be equal to value index. In the words of Fisher, each formula permit interchanging the prices and quantities without giving inconsistent results which means two results multiplied together should give the true value ratio. The test says that the change in price multiplied by change in quantity should be equal to total change in value. If P01 is a price index for the current year with reference to base year and Q₀₁is the quantity index for the current year. This test is satisfied by Fisher’s method only.Then by factor reversal test

Symbolically the test is represented as P₀₁ x Q₀₁ =  V₀₁, Where V₀₁ is the value index.

Let us see how Fishers ideal method satisfies the test.

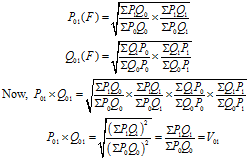
Thus Fisher’s method satisfies the factor reversal test

Note: Fisher’s method satisfies both the time reversal test and factor reversal test. Hence it is called the ideal index number.

Circular Test:

Another test of the adequacy of the index number formula is what is known as ‘circular test’. If in the use of index numbers interest attaches not merely to a comparison of two years, but to the measurement of price changes over a period of years. It is frequently desirable to shift the base. Clearly, the desirability of this property is that it enables us to adjust the index values from period to period without referring each time to the original base. A test of this shift ability of base. A test of this shift ability of base is called to the circular test. This test is just an extension of the time reversal test.

According to this, if indices are constructed for year one based on year zero, for year two based on year one and for year zero based on year two, the product of all the indices should be equal to 1.

Symbolically the test is represented as: P₀₁ X P₁₂ X P₂₀ = 1, This test is satisfied by

1. Simple aggregative method and
2. Kelly’s method.

Let us see how the simple aggregative method satisfies the test.

Thus the simple aggregative method satisfies the factor reversal test

Similarly, let us see how the fixed weight aggregative method satisfies the test.

Thus the fixed weight aggregative method satisfies the factor reversal test

An index which satisfies this test has the advantages of reducing the computations every time a change in the base year has to be made. Such index numbers can be adjusted from year to year without referring each time to the original bases. The circular test is not met by the ideal index or by any of weighted aggregative with changing weights. This test is met by the simple geometric mean of price relatives and the weighted aggregative fixed weights.