Science > Chemistry > States of Matter > Charle’s Law
Mathematical relationships between volume, pressure, and temperature of a given mass of gas are referred to as Gas laws. In this article. we shall study Charle’s Law.
Charle’s Law:
The relationship between the volume of a gas and temperature was observed by Jacques Charles in 1787.
Statement:
At constant pressure the volume of a given mass of a gas increases or decreases by 1/273 of its volume at 0oC for every degree rise or fall in temperature.
Explanation:
Let Vo be the volume of a gas at 0 °C, Let this gas be heated through t °C, Let Vt be the volume of the gas at t °C. then,
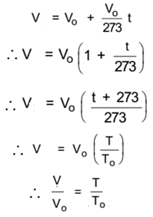
Thus V ∝ T
Alternate Statement of Charle’s Law:
Thus at constant pressure, the volume of the certain mass of enclosed gas is directly proportional to the absolute temperature of the gas.
In general

This relation is called the mathematical statement of Charle’s law.
Graphical Representation:
A graph is drawn by taking the absolute temperature on the x-axis and volume on the y-axis. The graph is as follows. This graph is also known as a V-T diagram.
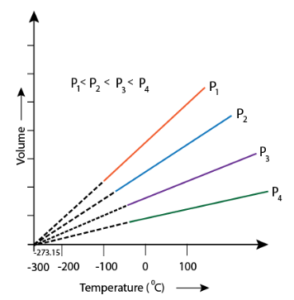
Each line of the graph represents different constant pressure. The lines are called isobar lines.
Charle’s Law and Kinetic Theory of Gases:
According to the kinetic theory of gases, gas consists of a large number of minute particles which are always in constant random motion. During this process, they collide with each other and with the walls of the container containing it. When molecules collide with the walls of the container, there is a change in the momentum of the colliding molecules. This is the cause of the pressure of the gas. According to the kinetic theory of gases, the kinetic energy of molecules is directly proportional to the absolute temperature of the gas.
Thus when gas is heated, the kinetic energy of molecules increases. Due to which the velocity of molecules increases, which results in more collision of the molecules with the walls of the container. But pressure is kept constant, hence the volume of the gas increases proportionally. Hence at constant pressure, the volume of a given mass of a gas is directly proportional to temperature.
Significance of Charle’s Law:
- Charle’s law is significant because it explains how gases behaviour at constant pressure and the relation between the absolute temperature and the volume of the gas. According to Charle’s law, at constant pressure, the volume and absolute temperature of a gas are directly proportional to each other.
- At constant pressure, the density of a gas is inversely proportional to its pressure.
- Using this concept hot air is used to fill the ballons used for meteorological purposes.
Numerical Problems:
Example – 01:
At 300 K a certain mass of a gas occupies 1 x 10-4 dm3 by volume. Calculate the volume of the gas at 450 K at the same pressure.
Given: Initial temperature = T1 = 300 K, Initial volume = V1 = 1 x 10-4 dm3 , Final temperature = T2 = 450 K
To Find: Final volume = V2 = ?
Solution:
By Charle’s Law

∴ V2 =(T2/T1) x V1
∴ V2 =(450/300) x 1 x 10-4 dm3 = (1.5) x 1 x 10-4 dm3 = 1.5 x 10-4 dm3
Ans: The volume of the gas at 450 K is 1.5 x 10-4 dm3
Example – 02:
The volume of a given mass of a gas at 0 °c is 2 dm3. Calculate the new volume of the gas at the constant pressure where (i) the temperature is increased by 10 °C (ii) the temperature is decreased by 10 °C.
Solution:
Part – I: the temperature is increased by 10 °C
Given: Initial temperature = T1 = 0 °C= 0 + 273.15 = 273.15 K, Initial volume = V1 = 2 dm3 , Final temperature = T2 = 0 °C + 10 °C = 10 °C = 10 + 273.15 = 283.15 K
To Find: Final volume = V2 = ?
By Charle’s Law

∴ V2 =(T2/T1) x V1
∴ V2 =(283.15/273.15) x 2 dm3 = 2.07 dm3
Part – II: the temperature is decreased by 10 °C
Given: Initial temperature = T1 = 0 °C= 0 + 273.15 = 273.15 K, Initial volume = V1 = 2 dm3 , Final temperature = T2 = 0 °C – 10 °C = – 10 °C = – 10 + 273.15 = 263.15 K
To Find: Final volume = V2 = ?
By Charle’s Law

∴ V2 =(T2/T1) x V1
∴ V2 =(263.15/273.15) x 2 dm3 = 1.93 dm3
Ans: When the temperature is increased by 10 °C, the new volume of gas is 2.07 dm3. When the temperature is decreased by 10 °C, the new volume of gas is 1.93 dm3
Example – 03:
A certain mass of a gas occupies a volume of 0.2 dm3 at 273 K. Calculate the volume of the gas if the absolute temperature is doubled at the same pressure.
Given: Initial temperature = T1 = 273 K, Initial volume = V1 = 0.2 dm3 , Final temperature = T2 = 2 x 273 = 546 K
To Find: Final volume = V2 = ?
Solution:
By Charle’s Law

∴ V2 =(T2/T1) x V1
∴ V2 =(546/273) x 0.2 dm3 = 0.4 dm3
Ans: When the temperature is doubled, the new volume of gas is 0.4 dm3
Example – 04:
When a ship is sailing in pacific ocean where the temperature is 23.4 °C, a balloon filled with 2.0 L of air. What will be the volume of the balloon when the ship reaches the Indian ocean, where the temperature is 26.1 °C.
Given: Initial temperature = T1 = 23.4 °C = 23.4 + 273 = 296.4 K, Initial volume = V1 =2.0 L, Final temperature = T2 = 26.1 °C = 26.1 + 273 = 299.1 K
To Find: Final volume = V2 = ?
Solution:
By Charle’s Law

∴ V2 =(T2/T1) x V1
∴ V2 =(299.1/296.4) x 2.0 L = 2.018 L
Ans: The volume of the balloon in the Indian ocean is 2.018 L.
Example – 05:
A sample of a gas occupies 10 dm3 at 127 °C and 1 bar pressure. The gas is cooled to – 73 °C at the same pressure. What will be the volume of the gas?
Given: Initial temperature = T1 = 127 °C = 127 + 273 = 400 K, Initial volume = V1 =10 dm3, Final temperature = T2 = – 73 °C = – 73 + 273 = 200 K
To Find: Final volume = V2 = ?
Solution:
By Charle’s Law

∴ V2 =(T2/T1) x V1
∴ V2 =(200/400) x 10 dm3 = 5 dm3
Ans: The new volume of the gas is 5 dm3
Example – 06:
A sample of gas is found to occupy a volume of 900 cm3 at 27 °C. Calculate the temperature at which it will occupy a volume of 300 cm3, provided the pressure is kept constant.
Given: Initial temperature = T1 = 27 °C = 27 + 273 = 300 K, Initial volume = V1 = 900 cm3 , Final volume = V2 =300 cm3
To Find: Final temperature = T2 = ?
Solution:
By Charle’s Law

∴ T2 =(V2/V1) x T1
∴ T2 =(300 cm3/900 cm3) x 300 K = 100 K
∴ T2 = 100 – 273 = -173 °C
Ans: At temperature -173 °C the volume is 300 cm3
Example – 07:
A gas occupies 100.0 mL at 50 °C and 1 atm pressure. The gas is cooled at constant pressure so that its volume is reduced to 50 mL. What is the final temperature?
Given: Initial temperature = T1 = 50 °C = 50 + 273 = 323 K, Initial volume = V1 = 100.0 mL , Final volume = V2 = 50.0 mL
To Find: Final temperature = T2 = ?
Solution:
By Charle’s Law

∴ T2 =(V2/V1) x T1
∴ T2 =(50.0 mL/100.0 mL) x 323 K = 161.5 K
∴ T2 = 150 – 273 = -111.5 °C
Ans: At temperature – 115.5 °C the volume is 50 mL.
Example – 08:
A gas occupies 100.0 mL at 50 °C and 1 atm pressure. The gas is cooled at constant pressure so that its volume is reduced to 50 mL. What is the final temperature?
Given: Initial temperature = T1 = 50 °C = 50 + 273 = 323 K, Initial volume = V1 = 100.0 mL , Final volume = V2 = 50.0 mL
To Find: Final temperature = T2 = ?
Solution:
By Charle’s Law

∴ T2 =(V2/V1) x T1
∴ T2 =(50.0 mL/100.0 mL) x 323 K = 161.5 K
∴ T2 = 150 – 273 = -111.5 °C
Ans: At temperature – 115.5 °C the volume is 50 mL.
Example – 09:
A vessel of capacity 400 cm3 contains hydrogen gas at 1 atm pressure and 7°C. In order to expel 28.57 cm3 of the gas the same pressure to what temperature the vessel should be heated?
Given: Initial temperature = T1 = 7 °C = 7 + 273 = 280 K, Initial volume = V1 = 400 cm3, Final volume = V2 = 400 cm3 + 28.57 cm3 = 428.57cm3.
To Find: Final temperature = T2 = ?
Solution:
By Charle’s Law

∴ T2 =(V2/V1) x T1
∴ T2 =(428.57 cm3/400.0 cm3) x 280 K = 300 K
∴ T2 = 300 – 273 = 27 °C
Ans: At temperature 27 °C, 28.57 cm3 of the gas expels.
Example – 10:
1 L of air weighs 1.293 g at 0 °C and 1 atm pressure. At what temperature 1 L of air at 1 atm pressure will weigh 1 g.
Given: Initial temperature = T1 = 0 °C = 0 + 273 = 273 K, Initial density = ρ1 = 1.293 g/L, Final density = ρ2 = 1 g/L.
To Find: Final temperature = T2 = ?
Solution:
By Charle’s Law

∴ T2 =(V2/V1) x T1
∴ T2 =((m/ρ2)/(m/ρ1)) x T1
∴ T2 =(ρ1/ρ2) x T1
∴ T2 =(1.293/1) x 273 = 353 K
∴ T2 = 353 – 273 = 27 °C
Ans: At temperature 80 °C, 1 L of air weighs 1 g