Science > Chemistry > Laws of Chemical Combinations > Gay-Lussac’s Law of Combining Volumes
In the previous article, we have studied the law of reciprocal proportions. In this article, we shall study Gay-Lussac’s Law of Combining Volumes. A French chemist Joseph L. Gay – Lussac in 1809, put forward this law.

Statement :
Whenever gases take part in a chemical reaction, either as reactants or as products, they do so in simple proportions by Volumes. Provided the volumes of gases are measured at the same temperature and pressure,
Illustration 1:
Consider following reaction
H2(g) + Cl2(g) → 2HCl
1vol 1vol 2 vol
Thus the simple ratio of volumes is 1 : 1 : 2
Illustration 2:
Consider following reaction
N2(g) + 3 H2(g) → 2NH3(g)
1vol 3vol 2 vol
Thus the simple ratio of volumes is 1 : 3 : 2
Numerical Problems:
Example – 01:
Calculate the volume of oxygen required for the complete combustion of 0.25 dm3 of methane at STP.
Solution:
CH4(g) + 2O2(g) → CO2(g) + 2H2O(g)
1 vol 2 vol 1 vol 2 vol
By Gay-Lussac’s law of combining volumes of gases
1 vol of methane requires 2 vol of oxygen for complete combustion.
Hence 0.25 dm3 of methane requires 2 x 0.25 = 0.50 dm3 of oxygen.
Example – 02:
Calculate the volume of hydrogen required for the complete hydrogenation of 0.25 dm3 of ethyne at STP.
Solution:
C2H2(g) + 2H2(g) → C2H6(g)
1 vol 2vol 1 vol
By Gay-Lussac’s law of combining volumes of gases
1 vol of ethyne requires 2 vol of hydrogen for complete hydrogenation.
Thus 0.25 dm3 of ethyne requires 2 x 0.25 = 0.50 dm3 of hydrogen for complete hydrogenation.
Example – 03:
Calculate the volume of hydrogen required for the complete hydrogenation of 0.25 dm3 of ethylene at STP.
Solution:
C2H4(g) + H2(g) → C2H6(g)
1 vol 1vol 1 vol
By Gay-Lussac’s law of combining volumes of gases
1 vol of ethylene requires 1 vol of hydrogen for complete hydrogenation.
Thus 0.25 dm3 of ethylene requires 1 x 0.25 = 0.25 dm3 of hydrogen for complete hydrogenation.
Example – 04:
Calculate the volume of oxygen required for the complete combustion of 0.25 mol of methane at STP.
Solution:
CH4(g) + 2O2(g) → CO2(g) + 2H2O(g)
1 mol 2 mol 1 mol 2 mol
By Gay-Lussac’s law of combining volumes of gases
1 mol of methane requires 2 mol of oxygen for complete combustion.
Thus 0.25 mol of methane requires 2 x 0.25 = 0.50 mol of oxygen.
One mole of any gas occupies 22.4 dm3 by volume at STP.
Volume of oxygen required = 22.4 x No. of moles = 22.4 x 0.5 = 11.2 dm3
Example – 05:
Calculate the volume of oxygen required for the complete combustion of 0.5 dm3 of H2S at STP.
Solution:
2H2S(g) + 3O2(g) → 2SO2(g) + 2H2O(g)
2 vol 3 vol 2 vol 2 vol
By Gay-Lussac’s law of combining volumes of gases
2 vol of H2S requires 3 vol of oxygen for complete combustion.
1 vol of H2S requires 3/2 = 1.5 vol of oxygen for complete combustion.
Thus 0.5 dm3 of H2S requires 1.5 x 0.5 = 0.75 dm3 of oxygen for complete combustion.
Example – 06:
Calculate the volume of oxygen required at STP for the complete combustion of 5.0 dm3 of ethane at 295 K and 0.993 x 105 Nm-2
Solution:
2C2H6(g) + 7O2(g) → 4CO2(g) + 6H2O(g)
2 vol 7 vol 4 vol 6 vol
By Gay-Lussac’s Law of Combining Volumes of gases
2 vol of C2H6 requires 7 vol of oxygen for complete combustion.
1 vol of C2H6 requires 7/2 = 3.5 vol of oxygen for complete combustion.
Thus 5 dm3 of C2H6 requires 3.5 x 5 = 17.5 dm3 of oxygen for complete combustion.
P = 0.993 x 105 Nm-2, T = 295 K, V = 17.5 dm3
Po = 1.013 x 105 Nm-2, To = 273 K, Vo = ?
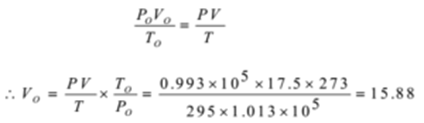
Thus the volume of oxygen required at STP is 15.88 dm3.
Example – 07:
6.0 dm3 of hydrogen is reacted with 2.4 dm3 of oxygen in a closed chamber. Calculate composition of resulting mixture.
Solution:
2H2(g) + O2(g) → 2 H2O(g)
2 vol 1 vol 2 vol
By Gay-Lussac’s law of combining volumes of gases.
The ratio of the volume of hydrogen to that of oxygen is 2 : 1.
In this case, oxygen is limiting reagent, and hydrogen is an excess reagent.
2.4 dm3 of oxygen can combine with 2 x 2.4 = 4.8 dm3 of hydrogen to form 2 x 2.4 = 4.8 dm3 of water vapours.
Thus unreacted hydrogen = 6.0 – 4.8 = 1. 2 dm3.
Thus resulting mixture contains 4.8 dm3 of water vapours and 1.2 dm3 of unreacted hydrogen.
Example – 08:
15 litres of nitrogen is made to react with 30 litres of hydrogen to prepare ammonia. Calculate composition of resulting mixture.
Solution:
N2(g) + 3 H2(g) → 2NH3(g)
1vol 3vol 2 vol
By Gay-Lussac’s law of combining volumes of gases
The ratio of the volume of nitrogen to that of hydrogen is 1 : 3.
In this case, hydrogen is limiting reagent, and nitrogen is an excess reagent.
3 x 10 = 30 litres of hydrogen can combine with 1 x 10 = 10 litres of nitrogen to form 2 x 10 = 20 litres of ammonia.
Thus unreacted nitrogen = 15.0 – 10.0 = 5 litres.
Thus resulting mixture contains 20 litres of ammonia and 5 litres of unreacted nitrogen.
Example – 09:
200 dm3 of hydrogen gas is allowed to react with 250 dm3 of chlorine gas. Calculate composition of resulting mixture.
Solution:
H2(g) + Cl2(g) → 2HCl
1vol 1vol 2 vol
By Gay-Lussac’s law of combining volumes of gases.
The ratio of the volume of hydrogen to that of chlorine is 1 : 1.
In this case, hydrogen is limiting reagent and chlorine is excess reagent.
200 dm3 of hydrogen can combine with 200 dm3 of chlorine to form 2 x 200 =400 dm3of hydrogen chloride.
Thus unreacted chlorine = 250 – 200 = 50 dm3.
Thus resulting mixture contains 400 dm3 of hydrogen chloride and 50 dm3 of unreacted chlorine.
Example – 10:
10 dm3 of hydrogen gas is allowed to react with 15 dm3 of chlorine gas. Calculate composition of resulting mixture.
Solution:
H2(g) + Cl2(g) → 2HCl
1vol 1vol 2 vol
By Gay-Lussac’s law of combining volumes of gases.
The ratio of the volume of hydrogen to that of chlorine is 1 : 1
In this case, hydrogen is limiting reagent and chlorine is excess reagent.
10 dm3 of hydrogen can combine with 10 dm3 of chlorine to form 2 x 10 = 20 dm3 of hydrogen chloride.
Thus unreacted chlorine = 15 – 10 = 5 dm3.
Thus resulting mixture contains 20 dm3 of hydrogen chloride and 5 dm3 of unreacted chlorine
In the next chaper we shall study the concept of atomic mass and equivalent mass.
Previous Topic: The Law of Reciprocal Proportions
Next Chapter: Concept of Atomic Mass and Equivalent Mass