Science > Chemistry > Molecule and Molecular Mass > Molecular Mass Using Ideal Gas Equation
In the last few articles, we have studied the molar volume method, Regnault’s method, and Graham’s diffusion law method to determine molecular mass. In this article, we shall study the ideal gas equation method to determine the molecular mass of a gas.
Molecule:
When two or more atoms are firmly held together by a chemical bond, a molecule is formed. The molecule of an element may consist of one or more atoms of the same kind, while that of the chemical compound consists of different kinds of atoms.
The smallest particle of an element or compound which can exist in a free state and does not take part in a chemical reaction is called molecule.
Molecules are denoted by formula indicating the number of constituent elements in the compound. For example molecular formula for oxygen is O2. Thus one molecule oxygen consists of two atoms of oxygen
Molecular Mass or Molar Mass:
The molecular mass or molar mass of a substance is defined as the ratio of the mass of one molecule of a substance to 1/12 th of the mass of 6C12 isotope taken as 12000 units.
Gram Molecular Mass or Molar Mass:
The molecular mass expressed in grams is called gram molecular mass (GMM)
Method – IV (Molecular Mass by Ideal Gas Equation / Law Method):
Principle:
The ideal gas equation is
PV = nRT
Where P = Pressure of the gas
V = Volume of the gas
n = Number of moles of the gas
R = Universal gas constant
T = Absolute temperature of the gas
Using the above relation and knowing the remaining quantities, the molecular mass can be calculated.
Numerical Problems:
Example – 01:
What is the relative molecular mass of the gas if 0.866 g sample is 60.0 ml. The bulb has a pressure of 400 mm at 20 °C. R = 0.0821 lit-atm
Given: w = 0.866 g, V = 60.0 ml = 60 x 10-3 dm3, P = 400 mm = 400/760 = 0.5263 atm
Solution:
By ideal gas equation. PV = nRT
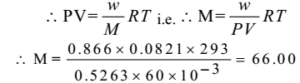
Ans: The relative molecular mass is 66.00
Example – 02:
0.1348 g of gas was found to occupy a volume of 25.80 ml at 0 OC and 760 mm of Hg pressure. calculate the relative molecular mass of the gas.
Given: w = 0. 1348 g, V = 25.80 ml = 25.80 x 10-3 dm3, P = 760 mm = 760/760 = 1 atm, T = 0 + 273 = 273 K
Solution:
By ideal gas equation PV = nRT
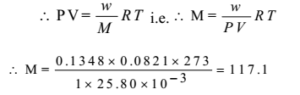
Ans: The relative molecular mass is 117.1
Example – 03:
3.895 dm3 of a gas at 293 K and 780 mm pressure were found to have a mass of 2.83 g. Calculate the relative molecular mass of the gas.
Given: w = 2.83 g, V = 3.895 dm3, P = 780 mm = 780/760 atm, T = 293 K
Solution:
By ideal gas equation, PV = nRT

Ans: The relative molecular mass is 17.03
Example – 04:
The molecular mass of a gaseous substance is 80. What will be the volume of 1 g of a gas at 0 °C and 720 mm mercury pressure? State whether this gas would diffuse through a porous pot slower or faster than chlorine.
Given: M = 80, w = 1 g, P = 720 mm = 720/760 atm, T = 0 +273 = 273 k
Solution:
By ideal gas equation, PV = nRT

The volume of the gas is 0.2957 dm3
By Graham’s diffusion law “The rate of diffusion of different gases under similar conditions of temperature and pressure are inversely proportional to square root of their densities”. In this case the molecular mass of the gas (80) is greater than the molecular mass of chlorine (71). Hence the gas will diffuse slowly.
Example – 05:
What is the relative molecular mass of the gas if 0.866 g sample is 60.0 ml. The bulb has a pressure of 400 mm at 20 °C. R = 0.0821 lit-atm
Given: w = 0.866 g, V = 60.0 ml = 60 x 10-3 litres, P = 400 mm = 400/760 = 0.5263 atm
Solution:
By ideal gas equation, PV = nRT

Ans: The relative molecular mass is 66.00