Molecular Mass Using Graham’s Law of Diffusion

Science > Chemistry > Molecule and Molecular Mass > Molecular Mass Using Graham’s Law of Diffusion

In the last few articles, we have studied the molar volume method and Regnault’s method to determine molecular mass. In this article, we shall study Graham’s law diffusion method to determine the molecular mass of a gas.

Molecule:

When two or more atoms are firmly held together by a chemical bond, a molecule is formed. The molecule of an element may consist of one or more atoms of the same kind, while that of the chemical compound consists of different kinds of atoms.

The smallest particle of an element or compound which can exist in a free state and does not take part in a chemical reaction is called molecule.

Molecules are denoted by formula indicating the number of constituent elements in the compound. For example molecular formula for oxygen is O₂. Thus one molecule oxygen consists of two atoms of oxygen

Molecular Mass or Molar Mass:

The molecular mass or molar mass of a substance is defined as the ratio of the mass of one molecule of a substance to 1/12 th of the mass of ⁶C₁₂ isotope taken as 12000 units.

Gram Molecular Mass or Molar Mass:

The molecular mass expressed in grams is called gram molecular mass (GMM)

Method – III (Molecular Mass by Graham’s Law Diffusion Method):

Principle:

Graham’s law of diffusion states that “The rate of diffusion of different gases under similar conditions of temperature and pressure are inversely proportional to the square root of their densities”.

But the densities are directly proportional to their molar masses. Hence the law can be restated as “The rate of diffusion of different gases under similar conditions of temperature and pressure are inversely proportional to square root of their molar masses”. Mathematically,

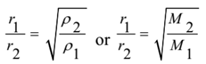
Numerical Problems:

Example – 01:

300 c.c. of oxygen gas takes 50 seconds to effuse through an aperture while the same volume of unknown gas takes 75 seconds. If the relative molecular mass of oxygen is 32, find the relative molecular mass of the unknown gas.

Given: Rate of diffusion of oxygen r_o = 300/50 = 6 c.c./s, Rate of diffusion of gas g = 300/75 = 4 c.c./s, The molecular mass of oxygen M_O = 32,

To Find: Molecular mass of gas M_g  =?

Solution:

By Graham’s law of diffusion

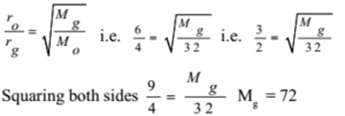
Ans: The molecular mass of the gas is 72.

Example – 02:

30 ml of ozone diffuses at the same time as 25 ml of chlorine. If the density of chlorine is 35.4. Find the density and relative molecular mass of ozone.

Given: Rate of diffusion of ozone r_O = 30 / t  ml per second, Rate of diffusion of chlorine r_Cl = 25 / t ml per second, Density of chlorine ρ_Cl = 35.4

To Find: Density of ozone ρ_O  =?, The Molecular mass of ozone M_O  =?

Solution:

By Graham’s law of diffusion

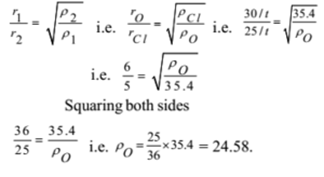
Ans: The molecular mass of the gas is 24.58

Example – 03:

In 75 seconds 400 ml of oxygen diffuses through a glass tube. If 25 seconds are taken by 100 ml of another gas ‘X’ to diffuse through the same tube under similar conditions. calculate the relative molecular mass of the gas ‘X’.

Given: Rate of diffusion of oxygen=  r_O = 400 / 75  = 16/3 ml per second, Rate of diffusion of gas ‘X’ = r_X = 100 /25 = 4  ml per second

Solution:

By Graham’s law of diffusion

Ans: The molecular mass of the gas is 56.9

Science > Chemistry > Molecule and Molecular Mass > Molecular Mass Using Graham’s Law of Diffusion