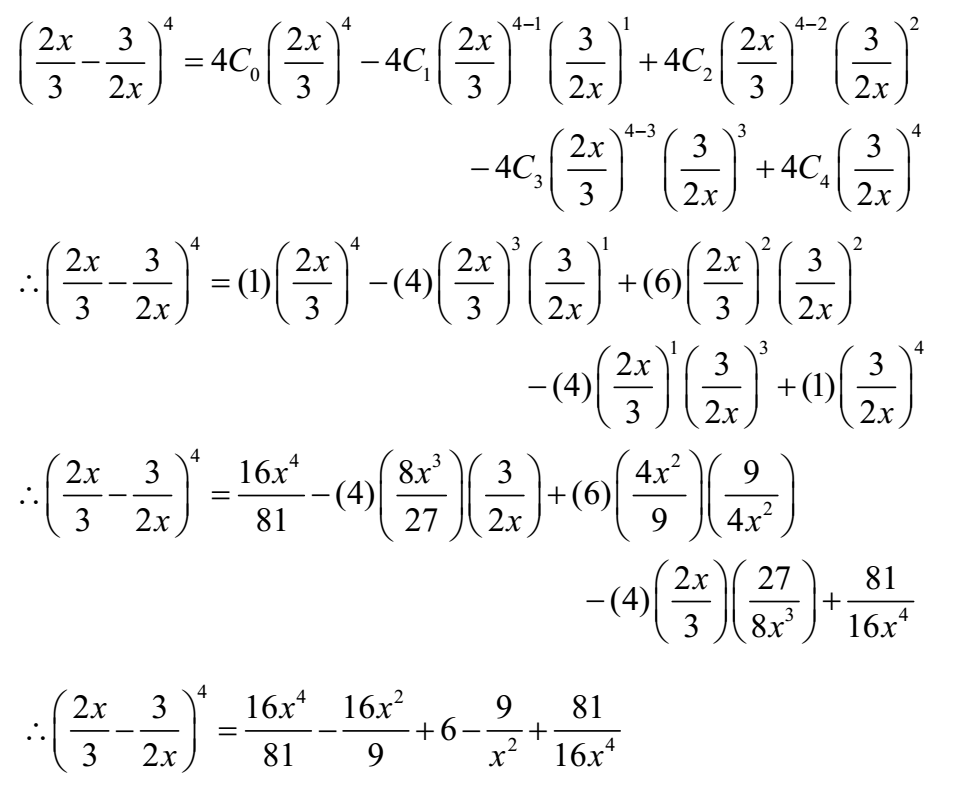Example 01:
Expand (a + b)2
Solution:
Expanding Binomially
(a + b)2 = 2C0a2 + 2C1a2-1b1 + 2C2b2
(a + b)2 = (1)a2 + (2)a1b1 + (1)b2
(a + b)2 = a2 + 2ab+ b2
Note: (a – b)2 = a2 – 2ab+ b2
Example 02:
Expand (a + b)3
Solution:
Expanding Binomially
(a + b)3 = 3C0a3 + 3C1a3-1b1 + 3C2a3-2b2 + 3C3b3
(a + b)3 = (1)a3 + (3)a2b1 + (3)a1b2 + (1)b3
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Note: (a – b)3 = a3 – 3a2b + 3ab2 – b3
Example 03:
Expand (a + b)4
Solution:
Expanding Binomially
(a + b)4 = 4C0a4 + 4C1a4-1b1 + 4C2a4-2b2 + 4C3a4-3b3 + 4C4b4
(a + b)4 = (1)a4 + (4)a3b1 + (6)a2b2 + (4)a1b3 + (1)b4
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Note: (a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4
Example 04:
Expand (a + b)5
Solution:
Expanding Binomially
(a + b)5 = 5C0a5 + 5C1a5-1b1 + 5C2a5-2b2 + 5C3a5-3b3 + 5C4a5-4b4 + 5C5b5
(a + b)5 = (1)a5 + (5)a4b1 + (10)a3b2 + (10)a2b3 + (5)a1b4 + (1)b5
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
Note: (a – b)5 = a5 – 5a4b + 10a3b2 – 10a2b3 + 5ab4 – b5
Example 05:
Expand (a + b)6
Solution:
Expanding Binomially
(a + b)6 = 6C0a6 + 6C1a6-1b1 + 6C2a6-2b2 + 6C3a6-3b3 + 6C4a6-4b4 + 6C5a6-5b5 + 6C6b6
(a + b)6 = (1)a6 + (6)a6-1b1 + (15)a6-2b2 + (20)a6-3b3 + (15)a6-4b4 + (6)a6-5b5 + (1)b6
(a + b)6 = a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6
Note: (a – b)6 = a6 – 6a5b + 15a4b2 – 20a3b3 + 15a2b4 – 6ab5 + b6
Example 06:
Expand (2x + 3y)4
Solution:
Expanding Binomially
(2x + 3y)4 = 4C0(2x)4 + 4C1(2x)4-1(3y)1 + 4C2(2x)4-2(3y)2 + 4C3(2x)4-3(3y)3 + 4C4(3y)4
(2x + 3y)4 = (1) (2x)4 + (4) (2x)3(3y)1 + (6) (2x)2(3y)2 + (4) (2x)1(3y)3 + (1) (3y)4
(2x + 3y)4 = 16x4 + (4) (8x3) (3y) + (6) (4x2) (9y2) + (4) (2x)(27y3) + (1) (81y4)
(2x + 3y)4 = 16x4 + 96x3y + 216x2y2 + 216xy3 + 81y4
(2x – 3y)4 = 16x4 – 96x3y + 216x2y2 – 216xy3 + 81y4
Example 07:
Expand (3x – 2y)4
Solution:
Expanding Binomially
(3x – 2y)4 = 4C0(3x)4 – 4C1(3x)4-1(2y)1 + 4C2(3x)4-2(2y)2 – 4C3(3x)4-3(2y)3 + 4C4(2y)4
(3x – 2y)4 = (1) (3x)4 – (4) (3x)3(2y)1 + (6) (3x)2(2y)2 – (4) (3x)1(2y)3 + (1) (2y)4
(3x – 2y)4 = (1) (81x4) – (4) (27x3) (2y) + (6) (9x2) (4y2) – (4) (3x)(8y3) + (1) (16y4)
(3x – 2y)4 = 81x4 – 216x3y + 216x2y2 – 96xy3 + 16y4
(3x + 2y)4 = 81x4 + 216x3y + 216x2y2 + 96xy3 + 16y4
Example 08:
Expand (x2 – 2y)5
Solution:
Expanding Binomially
(x2 – 2y)5= 5C0(x2)5 – 5C1(x2)5-1(2y)1 + 5C2(x2)5-2(2y)2 – 5C3(x2)5-3(2y)3 + 5C4(x2)5-4(2y)4 – 5C5(2y)5
(x2 – 2y)5= (1) (x10) – (5) (x8)(2y) + (10) (x6)(4y2) – (10) (x4)(8y3) + (5) (x2) (16y4) – (1) (32y5)
(x2 – 2y)5= x10 – 10x8y + 40x6y2 – 80x4y3 + 80x2y4 – 32y5
Example 09:
Expand (2x2 + 3)4
Solution:
Expanding Binomially
(2x2 + 3)4 = 4C0(2x2)4 + 4C1(2x2)4-1(3)1 + 4C2(2x2)4-2(3)2 + 4C3(2x2)4-3(3)3 + 4C4(3)4
(2x2 + 3)4 = (1)(2x2)4 + (4)(2x2)3(3)1 + (6)(2x2)2(3)2 + (4)(2x2)1(3)3 + (1)(3)4
(2x2 + 3)4 = (16x8) + (4)(8x6)(3) + (6)(4x4) (9) + (4)(2x2) (27) + 81
(2x2 + 3)4 = 16x8 + 96x6 + 216x4 + 216x2 + 81
Example 10:
Expand (2x + y)4
Solution:
Expanding Binomially
(2x + y)4 = 4C0(2x)4 + 4C1(2x)4-1(y)1 + 4C2(2x)4-2(y)2 + 4C3(2x)4-3(y)3 + 4C4(y)4
(2x + y)4 = (1) (2x)4 + (4) (2x)3(y)1 + (6) (2x)2(y)2 + (4) (2x)1(y)3 + (1) (y)4
(2x + y)4 = 16x4 + (4) (8x3) (y) + (6) (4x2) (y2) + (4) (2x) (y3) + (1) (y4)
(2x + y)4 = 16x4 + 32x3y + 24x2y2 + 8xy3 + y4
Example 11:
Expand (x – 2y)4
Solution:
Expanding Binomially
(x – 2y)4 = 4C0(x)4 – 4C1(x)4-1(2y)1 + 4C2(x)4-2(2y)2 – 4C3(x)4-3(2y)3 + 4C4(2y)4
(x – 2y)4 = (1) (x4) – (4) (x3) (2y) + (6) (x2) (4y2) – (4) (x)(8y3) + (1) (16y4)
(x – 2y)4 = x4 – 8x3y + 24x2y2 – 32xy3 + 16y4
Example 12:
Expand (x + 1)6
Solution:
Expanding Binomially
(x + 1)6 = 6C0(x)6 + 6C1(x)6-1(1)1 + 6C2(x)6-2(1)2 + 6C3(x)6-3(1)3 + 6C4(x)6-4(1)4 + 6C5(x)6-5(1)5 + 6C6(1)6
(x + 1)6 = (1)(x)6 + (6)(x)5(1)1 + (15)(x)4(1)2 + (20)(x)3(1)3 + (15)(x)2(1)4 + 6(x)1(1)5 + (1)(1)6
(x + 1)6 = x6 + 6x5+ 15x4+ 20x3 + 15x2+ 6x + 1
Example 12:
Expand (x – 1)6
Solution:
Expanding Binomially
(x – 1)6 = 6C0(x)6 – 6C1(x)6-1(1)1 + 6C2(x)6-2(1)2 – 6C3(x)6-3(1)3 + 6C4(x)6-4(1)4 – 6C5(x)6-5(1)5 + 6C6(1)6
(x – 1)6 = (1)(x)6 – (6)(x)5(1)1 + (15)(x)4(1)2 – (20)(x)3(1)3 + (15)(x)2(1)4 – 6(x)1(1)5 + (1)(1)6
(x – 1)6 = x6 – 6x5+ 15x4– 20x3 + 15x2 – 6x + 1
Example 12:
Expand (3x2 + 2y)5
Solution:
Expanding Binomially
(3x2 + 2y)5 = = 5C0(3x2)5 + 5C1(3x2)5-1(2y)1 + 5C2(3x2)5-2(2y)2 + 5C3(3x2)5-3(2y)3 + 5C4(3x2)5-4(2y)4 + 5C5(2y)5
(3x2 + 2y)5 = (1) (3x2)5 + (5) (3x2)4(2y)1 + (10) (3x2)3(2y)2 + (10) (3x2)2(2y)3 + (5) (3x2)1(2y)4 + (1) (2y)5
(3x2 + 2y)5 = (1) (243x10) + (5) (81x8) (2y) + (10) (27x6) (4y2) + (10) (9x4)(8y3) + (5) (3x2) (16y4) + (1) (32y5)
(3x2 + 2y)5 = 243x10 + 810x8y + 1080x6y2 + 720x4y3 + 240x2y4 + 32y5
Example 13:
Expand (x + 1/x)6
Solution:
Expanding Binomially
(x + 1/x)6= 6C0(x)6 + 6C1(x)6-1(1/x)1 + 6C2(x)6-2(1/x)2 + 6C3(x)6-3(1/x)3 + 6C4(x)6-4(1/x)4 + 6C5(x)6-5(1/x)5 + 6C6(1/x)6
(x + 1)6 = (1)(x)6 + (6)(x)5(1/x)1 + (15)(x)4(1/x)2 + (20)(x)3(1/x)3 + (15)(x)2(1/x)4 + 6(x)1(1/x)5 + (1)( 1/x)6
(x + 1)6 = x6 + 6x5(1/x) + 15x4(1/x2) + 20x3(1/x3) + 15x2(1/x4) + 6x(1/x5) + 1/x6
(x + 1)6 = x6 + 6x4 + 15x2 + 20 + 15/x2 + 6/x4 + 1/x6
Example 14:
Expand (2x – 1/x)5
Solution:
Expanding Binomially
(2x – 1/x)5 = 5C0(2x)5 – 5C1(2x)5-1(1/x)1 + 5C2(2x)5-2(1/x)2 – 5C3(2x)5-3(1/x)3 + 5C4(2x)5-4(1/x)4 – 5C5(1/x)5
(2x – 1/x)5 = (1)(2x)5 – (5)(2x)4(1/x)1 + (10)(2x)3(1/x)2 – (10)(2x)2(1/x)3 + (5)(2x)1(1/x)4 – (1)(1/x)5
(2x – 1/x)5 = 32x5 – (5)(16x4) (1/x) + (10)(8x3) (1/x2) – (10)(4x2) (1/x3) + (5)(2x) (1/x4) – (1)(1/x5)
(2x – 1/x)5 = 32x5 – 80x3 + 80x – 40/x + 10/x3 – 1/x5
Example 15:
Expand (x2 + 1/x2)5
Solution:
Expanding Binomially
(x2 + 1/x2)5 = 5C0(x2)5 – 5C1(x2)5-1(1/x2)1 + 5C2(x2)5-2(1/x2)2 – 5C3(x2)5-3(1/x2)3 + 5C4(x2)5-4(1/x2)4 – 5C5(1/x2)5
(x2 + 1/x2)5 = (1)( x2)5 – (5)( x2)4(1/x2)1 + (10)( x2)3(1/x2)2 – (10)( x2)2(1/x2)3 + (5)( x2)1(1/x2)4 – (1)( 1/x2)5
(x2 + 1/x2)5 = x10 – (5)( x8)(1/x2) + (10)( x6)(1/x4) – (10)( x4)(1/x6) + (5)( x2) (1/x8) – 1/x10
(x2 + 1/x2)5 = x10 – 5 x6 + 10x2 – 10/x2 + 5/x6 – 1/x10
Example 6:
Expand (2x/3 – 3/2x)4
Solution:
Expanding Binomially