Science > Mathematics > Algebra > Logarithms > Concept of Logarithm
In this article, we shall study the concept of logarithms and interconversion between exponential form and logarithmic form.
Laws of Indices:
- am × an = am + n
- am ÷ an = am – n (a ≠ 0)
- (am)n = amn
- (ab)m = am × bm
- (a ÷ b)m = am ÷ bm (b ≠ 0)
- a-m = 1/am (a ≠ 0)
- a0 = 1
Definition of Logarithm:
If m = ax, where a > 0 and m > 0 then x is called the logarithm of m to the base a and is written as x = logam and read as a log of m to the base a where m, a, x are real numbers.
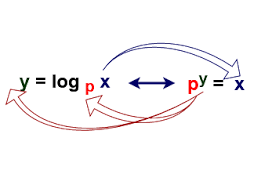
Notes:
- The logarithm of a negative number and zero are not defined.
- Logarithm to the base 10 are called common or Briggsian logarithms.
- Logarithms to the base e, where e is an irrational number whose value is e = 2.7182… are called natural or Naperian logarithms.
Conversion from the Exponential Form into Logarithmic Form:
| Exponential Form | Logarithmic Form |
| ab = c | logac = b |
| 52 = 25 | log525 = 2 |
| 91/2 = 3 | log93 = 1/2 |
| (27)1/3 = 3 | log273 = 1/3 |
| 10-3 = 1/1000 | log10(1/1000) = -3 |
| 70 = 1 | log71 = 0 |
| 83 = 512 | log8512 = 3 |
| 323/5 = 8 | log328 = 3/5 |
| 7-2 = 1/49 | log7(1/49) = -2 |
| 10-2 = 1/100 | log10(1/100) = -2 |
| 25 = 32 | log232 = 5 |
| 9-1/2 = 1/3 | log9(1/3) = -1/2 |
| 23 = 8 | log28 = 3 |
| 10-1 = 0.1 | log10(0.1) = -1 |
| 4-2 = 1/16 | log4(1/16) = -2 |
| 80 = 1 | log81 =0 |
| 53 = 125 | log5125 = 3 |
| 27-1/3 = 1/9 | log27(1/9) = -1/3 |
| 95/2 = 243 | log9243 = 5/2 |
| 4-3 = 1/64 | log4(1/64) = -3 |
Conversion from the Logarithmic Form into the Exponential Form:
| Logarithmic Form | Exponential Form |
| log100.0001 = – 4 | 10-4 = 0.0001 |
| log2128 = 7 | 27 = 128 |
| log816 = 4/3 | 84/3 = 16 |
| log96561 = 4 | 94 = 6561 |
| log(1/16)(1/8) = 3/4 | (1/16)3/4 = 1/8 |
| log2(1/4) = -2 | 94 = 6561 |
| log0.50.125 = 3 | 0.53 = 0.125 |
| logqp = r | qr = p |
| log232 = 5 | 25 = 32 |
| log(1/2)(1/8) = 3 | (1/2)3 = 1/8 |
| log279 = 2/3 | 272/3 = 9 |
| log7343 = 3 | 73 = 243 |
| log33 = 1 | 31 = 3 |
| log6(1/36) = -2 | 6-2 = 1/36 |
| log81(1/3) = – 1/4 | 81– 1/4 = 1/3 |
In the next article, we shall study to solve the problems based on the definition of a logarithm.