In last few articles, we have studied arithmetic progression. In this article, we shall study geometric progression (G.P.).
A sequence (tn) is said to be a geometric progression (G.P.) if the ratio
tn + ! /tn = constant for all n ∈ N
The constant ratio is called the common ratio of the G.P. and is denoted by letter ‘r’. The first term is denoted by the letter ‘a’.
General Term or nth Term of a Geometric Progression:
If ‘a’ is the first term and ‘r’ is the common ratio of the G.P,. then the nth term is given by
tn = a rn- 1
Find tn for Geometric Progression (G.P.):
Example – 01:
Find nth term of a geometric progression (G.P.) 2, 6, 18, 54, …..
Solution:
Given G.P. is 2, 6, 18, 54, …..
First term = a = 2, common ratio = r = 6/2 = 3
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 2 (3)n- 1
Ans: The nth term of the G.P. is 2 (3)n- 1
Example – 02:
Find nth term of a geometric progression (G.P.) 25, 5, 1, 1/5, …..
Solution:
Given G.P. is 25, 5, 1, 1/5, …..
First term = a = 25, common ratio = r = 5/25 = 1/5
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 25 (1/5)n- 1 = 52 (1/5)n- 1 = (1/5)-2 (1/5)n- 1 = (1/5)n- 3
Ans: The nth term of the G.P. is (1/5)n- 3
Example – 03:
Find nth term of a geometric progression (G.P.) 3, 3, 3, 3, …..
Solution:
Given G.P. is 3, 3, 3, 3, …..
First term = a = 3, common ratio = r = 3/3 = 1
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 3 (1)n- 1 = 3 x 1 = 3
Ans: The nth term of the G.P. is 3
Example – 04:
Find nth term of a geometric progression (G.P.) 3, 15, 75, 375, …..
Solution:
Given G.P. is 3, 15, 75, 375, …..
First term = a = 3, common ratio = r = 15/3 = 5
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 3(5)n- 1
Ans: The nth term of the G.P. is 3(5)n- 1
Example – 05:
Find nth term of a geometric progression (G.P.) 1, -4, 16, -64, …..
Solution:
Given G.P. is 1, -4, 16, -64, …..
First term = a = 1, common ratio = r = -4/1 = – 4
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 1(- 4)n- 1 = (- 4)n- 1
Ans: The nth term of the G.P. is (- 4)n- 1
Example – 06:
Find nth term of a geometric progression (G.P.) 1, -3/2, 9/4, – 27/8, …..
Solution:
Given G.P. is 1, -3/2, 9/4, – 27/8, …..
First term = a = 1, common ratio = r = (-3/2)/1 = – 3/2
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 1(- 3/2)n- 1 = (- 3/2)n- 1
Ans: The nth term of the G.P. is (- 3/2)n- 1
Example – 06:
Find nth term of a geometric progression (G.P.) √3, 1/√3, 1/3√3, 1/9√3, …..
Solution:
Given G.P. is √3, 1/√3, 1/3√3, 1/9√3, …..
First term = a = √3, common ratio = r = (1/√3)/√3= 1/3
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = √3(1/3)n- 1
∴ tn = (3)1/2(1/3)n- 1 = (1/3)-1/2(1/3)n- 1
∴ tn = (1/3)n- 3/2
Ans: The nth term of the G.P. is (1/3)n- 3/2
Example – 07:
Show that the sequence 3, 6, 12, 24, 48, ….. is a G.P. Find the 7th term.
Solution:
Given sequence is 3, 6, 12, 24, 48, …..
t2/t1 = 6/3 = 2, t3/t2 = 12/6 = 2, t4/t3 = 24/12 = 2, t5/t14 = 48/24 = 2,
Thus in given sequence the ratio of next term to the previous term is constant and is equal to 2
Hence the given sequence is a G.P.
First term = a = 3, common ratio = r = 2
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 3(2)n- 1
∴ t7 = a rn- 1 = 3(2)7- 1 = 3(2)6 = 3 x 64 = 192
Ans: The 7th term of the G.P. is 192
Example – 08:
If a = 7, r = 1/3, find t6.
Solution:
Given first term = a = 7, common ratio = r = 1/3
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 7(1/3)n- 1
∴ t6 = 7(1/3)6- 1 = 7(1/3)5 = 7(1/243)= 7/243
Ans: t6. = 7/243
Example – 09:
If a = 5, r = – 2, find t5.
Solution:
Given first term = a = 5, common ratio = r = – 2
the nth term of a G.P. is given by tn = a rn- 1
∴ tn = a rn- 1 = 5(- 2)n- 1
∴ t5 = 5(- 2)5- 1 = 5(-2)4 = 5 x 16 = 80
Ans: t5. = 80
Example – 10:
If a = 2/3, t6 = 162, find r.
Solution:
Given first term = a = 2/3, t6 = 162
the nth term of a G.P. is given by tn = a rn- 1
∴ t6 = (2/3) r6- 1
∴ 162 = (2/3) r5
∴ (162 x 3)/2= r5
∴ r5 = 81 x 3= 243
∴ r = 3
Ans: r = 3
Example – 11:
If r = 2, t8 = 640, find a.
Solution:
Given fcommon ratio = r = 2, t8 = 640
the nth term of a G.P. is given by tn = a rn- 1
∴ t8 = a (2)8- 1
∴ 640 = a x 27
∴ 640 = 128 a
∴ a = 5
Ans: a = 5
Example – 12:
If a = 5, t6 = 1/625, find r and t10.
Solution:
Given first term = a = 5, t6 = 1/625
the nth term of a G.P. is given by tn = a rn- 1
∴ t6 = 5 r6- 1
∴ 1/625 = (5) r5
∴ 1/3125= r5
∴ r= 1/5
Now, tn = a rn- 1
t10 = 5(1/5)10 – 1 (1/5)– 1(1/5)9 = (1/5)8 = 1/390625
Ans: r = 1/5 and t10 = (1/5)8 = 1/390625
Example – 13:
If for a sequence, tn = 4n – 3/5n – 2, show that the sequence is G.P. and find the first term and common ratio.
Solution:

Thus in given sequence the ratio of next term to the previous term is constant and is equal to 4/5
Hence the given sequence is a G.P. and its common ratio = r = 4/5
the nth term of a G.P. is given as tn = 4n – 3/5n – 2
t1 = 41 – 3/51 – 2 = 4-2/5-1 = 51/42 = 5/16
Ans: First term = 5/16 and common ratio = 4/5
Example – 14:
If for a sequence, tn = 2n – 2/5n – 3, show that the sequence is G.P. and find the first term and common ratio.
Solution:
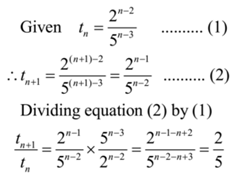
Thus in given sequence the ratio of next term to the previous term is constant and is equal to 2/5
Hence the given sequence is a G.P. and its common ratio = r = 25
the nth term of a G.P. is given as tn = 2n – 2/5n – 3
t1 = 21 – 2/51 – 3 = 2-1/5-2 = 52/21 = 25/2
Ans: First term = 25/2 and common ratio = 2/5
Example – 15:
If for a sequence, tn = (-5)n +1/3n – 1, show that the sequence is G.P. and find the first term and common ratio.
Solution:
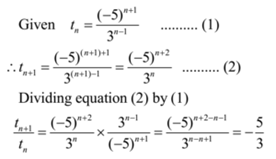
Thus in given sequence the ratio of next term to the previous term is constant and is equal to – 5/3
Hence the given sequence is a G.P. and its common ratio = r = – 5/3
the nth term of a G.P. is given as tn = (-5)n +1/3n – 1
t1 = (-5)1 +1/31 – 1 = (-5)2/30 = 25/1 = 25
Ans: First term = 25 and common ratio = – 5/3