A set is a collection of well-defined objects. These objects may be actually listed or may be specified by a rule. Sets are denoted by a capital letter like A, B, C…. and an object belonging to them (element of the set) are denoted by a small case letter like a, b, c,… of the alphabet. Certain standard letters used for particular sets are:
- N = Set of natural numbers = {1, 2, 3, 4, …},
- I = Set of integers = {…., -3, -2, -2, 0, 1, 2, 3, ……}
- Q = Set of rational numbers and
- R = Set of real numbers.
Elements of a Set:
If an object ‘a’ belongs to set A, this is written as ‘a ∈ A’ and read as ‘a belongs to set A’. The symbol ‘∈’ is a Greek letter ‘epsilon’ and is used to denote “belongs to”. Obviously, ∉ will mean “does not belong to”.
Example 1:
A = {1, 2, 3, 4, 5}
Then ‘3 belongs to set A’ can be written as 3 ∈ A similarly ‘8 does not belong to set A’ is written as 8 ∉ A.
Example 2:
B = Set of all the days in a week = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
Then ‘Friday belongs to set B’ can be written as Friday ∈ A. Similarly, ‘January does not belong to B’ can be written as January ∉ B.
Number of Elements in a Set:
If A is a set then n(A) denotes the total number of elements in it provided it is finite.
Order or Cardinality of Set:
The order of a set defines the number of elements a set is having. It describes the size of a set. The order of set is also known as the cardinality of the set. The size of set whether it is is a finite set or an infinite set said to be set of finite order or infinite order, respectively.
B = Set of all the days in a week = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
This set has 7 elements, hence the order of set B or cardinality of set B is 7. It has finite order.
N = Set of natural numbers = {1, 2, 3, 4, ……..}
In this set there are infinite number of elements, hence the set has infinite order.
Representation of Sets:
Sets can be represented in two ways:
- Roster Method or Tabular form
- Set Builder Notation or Rule Method
Roster Method or Tabular Form:
In roster form, all the elements of the set are listed, separated by commas and enclosed between curly braces { }. Here each element of the set is listed.
Consider set A = {1, 2, 3, 4, 5}.
In this case, we are given a list of objects that belong to A. An object which is not included in this list will not be in A. Elements are separated by commas. Such a method of specifying a set is called the Roster method or Tabular method.
N = {1, 2, 3, 4, 5, ….} gives the set of natural numbers. Since it is impossible to list all the elements (natural numbers), the list is not completely given but the dots indicate that similar numbers (natural numbers) are included in this set.
“Set Builder Notation” or “Rule Method”:
The set A = {1, 2, 3, 4, 5) can also be written as
A = The set of natural numbers from 1 to 5 including 1 and 5.
Hence we could have stated that : “x is a member of set A if x is a natural number and 1 less than equal to x less than equal to 5”. This long sentence can be written, in short as
A = {x| x ∈ N, 1 ≤ x ≤ 5}
which is read as: A is the set of objects x such that x Î N and 1 ≤ x ≤ 5.
In general, if a set X contains objects having a property P in common, we write X in set builder notation as :
X = {x| x has property P}.
The set builder notation is very important as, in writing down many sets, where the roster method cannot be used.
For example, E = {x| x ∈ Q, 1 ≤ x ≤ 5} cannot be written by roster method but this can be clearly written and understood in the set-builder notation.
Let us write down some sets in the set builder notation and convert them into the roster method.
A = {x| x ∈ I, -3 ≤ x ≤ 3} means A = {-3, -2, -1, 0, 1, 2, 3}.
B = {y| y ∈ N, 2 < x ≤ 7} means B = {3, 4, 5, 6, 7}.
C = {z| z is a vowel in English alphabet} means C = {a, e, i, o, u}
Types of Sets:
Singleton Set:
A set containing only one element is a singleton set,
Examples:
- the set {a} is a singleton set.
- The set A = set of all integers which are neither positive nor negative.” is a singleton set, as A = {0}. n(A) = 1, thus the order of the set is 1.
Null Set or Empty Set:
A set containing no element is called a null set [or an empty set]. It is usually denoted as f or { }.
Examples:
- the set of all real numbers whose square is negative is a null set,
- the set {x | x Î N, 3 < x < 4} is a null set,
Note: The set {0} is not a null set as it contains one element, namely zero.
Finite Set:
A set which consists of a definite number of elements is called a finite set.
Example:,A = {1,2,3,4,5,6,7,8,9,10}
In this set there are 10 elements which can be counted. Thus n(A) = 10. The order of set A is 10. It is a finite set.
Infinite Set:
A set which is not finite is called an infinite set.
Example: N = set of all the natural numbers.
N = {1,2,3,4,5,6,7,8,9……}
In this set number of elements cannot be counted. Set N is of an infinite order. Hence set N is infinite set.
Equivalent Sets:
If the number of elements is the same for two different sets, then they are called equivalent sets. It is represented as: n(A) = n(B)
Where, A and B are two different sets with the same number of elements.
Example: If A = {1, 2, 3, 4} and B = {Red, Blue, Green, Black}
In set A, there are four elements i.e. n(A) = 4 and in set B also there are four elements i.e. n(B) = 4. Thus n(A) = n(B). Therefore, set A and set B are equivalent.
Note: The elements of the two sets may be the same or different, but the number of elements in the set is equal i.e. their order should be the same.
Equal Sets:
The two sets A and B are said to be equal if they have exactly the same elements, the order of elements do not matter.
Example: A = {1, 2, 3, 4} and B = {4, 3, 2, 1}
Mathematically, A = B
If A = {x| x is a letter in the word LET} = {L, E, T}, and
B = [{x| x is a letter in the word TELE} = {T, E, L},
Mathematically, A = B
A = {x| x is a letter in the word WOLF} = {W, O, L, F}
B = {x| x is a letter in the word FOLLOW} = {F, O, L, W}
Mathematically, A = B
In general sets, A and B are equal if and only if A ⊆ B and B ⊆ A
Disjoint Sets:
The two sets A and B are said to be disjoint if the set does not contain any common element.
Example: Set A = {1, 2, 3, 4} and set B = {5, 6, 7, 8} are disjoint sets, because there is no common element between them.
Subset:
Consider the sets A = {1, 2, 3}, B = {1, 2, 3, 4, 5}.
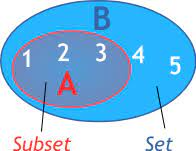
We note that every element of set A is an element of set B. This can be expressed ordinarily as: ‘A is a part of B.’ We express this in set theory as ‘A is a subject of B’ and write it as A ⊆ B.
We can define A ⊆ B as follows: We can say that A ⊆ B, if and only if every element of set A is an element of set B’. This in notation can be written as: A ⊆B if and only if, for every x ∈ A, it is true that x ∈ B.
Example:
If A = {x| x is a letter in the word LET} = {L, E, T} and B = [{x| x is a letter in the word LETTER} = {L, E, T, R},
A ⊆ B
Note: If A = {1, 2, 3} then {}, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, and {1, 2, 3} are subsets of A.
Proper Subset:
If A and B are two sets for which A ⊆ B is true but B ⊆ A is not true we say that A is a proper subset of B and write it as A ⊂ B. Since B ⊆ A is not true, B must have at least one element not belonging to A.
Hence we can give the definition: We say that A ⊂ B if and only if
- every element of A is an element of B, and
- B has at least one element in it which does not belong to A.
Note: In usual notation N ⊂ W ⊂ I ⊂ Q ⊂ R
Superset:
If set A is a subset of set B and all the elements of set B are the elements of set A, then A is a superset of set B. It is denoted by A ⊃ B.
Example: If Set A = {1, 2, 3, 4} is a subset of B = {1, 2, 3, 4}. Then A is superset of B.
Universal Set:
A set which contains all the sets relevant to a certain condition is called the universal set. It is the set of all possible values.
Example: If A = {1, 2, 3} and B = {2, 3, 4, 5}, then universal set here will be:
U = {1, 2, 3, 4, 5}
Power Set:
In set theory, the power set of a Set A is defined as the set of all subsets of the Set A including the Set itself and the null or empty set. It is denoted by P(A).
If A = {1, 2, 3} then {}, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, and {1, 2, 3} are subsets of A.
Then power set of A = P(A) = {{}, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}}
The number of elements in the power set of A = 2n, where n is the order of set A.
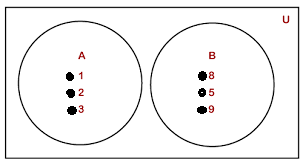
Venn Diagram:
A set can be represented by a closed figure like a circle, a triangle, etc. Such a representation is called the Venn diagram. The points inside the figure represent the members of the set.
Summary of Terminology and Notations of Sets:
| Symbol | Symbol Name |
| { } | set |
| A ∪ B | A union B |
| A ∩ B | A intersection B |
| A ⊆ B | A is subset of B |
| A ⊄ B | A is not subset B |
| A ⊂ B | A proper subset / strict subset of B |
| A ⊃ B | A proper superset / strict superset of B |
| A ⊇ B | A superset of B |
| A ⊅ B | A not superset of B |
| Ø | Empty set |
| P (C) | Power set |
| A = B | Equal set |
| Ac | Complement of A |
| a ∈ B | a element of B |
| x ∉ A | x not element of A |