Use of the Laws of Logarithms: Set – I

Science > Mathematics > Algebra > Logarithms > Use of the Laws of Logarithms Set – I

In the last article, we have studied the laws of logarithms and their proofs. In this article, we shall study to solve problems on laws of logarithms (law of product, Law of quotient, Law of exponent, etc.) to evaluate or simplify given logarithmic expression.

Laws of Logarithms

• Log a + Log b = Log (ab) (Law of Product)
• Log a – log b = log (a/b)    b ≠ 0 (law of Quotient)
• Log a^m = m Log a (Law of exponent)
• Log (1) = 0
• Log_aa = 1
• 
• 
• 

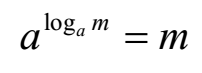
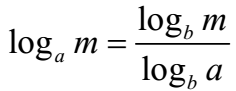
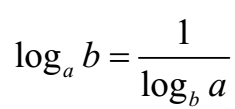
Example 01:

• Simplify log₁₀5 + 2 log₁₀4

Solution:

log₁₀5 + 2 log₁₀4

= log₁₀5 + log₁₀4² (Law of exponent)

= log₁₀5 + log₁₀16

= log₁₀(5 x 16) (Law of product)

= log₁₀80

Ans: log₁₀5 + 2 log₁₀4 = log₁₀80

Example 02:

• Simplify 2 log 7 – log 14

Solution:

2 log 7 – log 14

= log 7² – log 14 (Law of exponent)

= log 49 – log 14

= log (49/14) (Law of quotient)

= log (7/2)

Ans: 2 log 7 – log 14 = log (7/2)

Example 03:

• Simplify log₁₀3 + log ₁₀2 – 2log₁₀5

Solution:

log₁₀3 + log ₁₀2 – 2log₁₀5

= log₁₀3 + log ₁₀2 –log₁₀5² (Law of exponent)

= log₁₀3 + log ₁₀2 –log₁₀25

= log₁₀((3 x 2)/25) (Law of product and quotient)

= log₁₀(6/25)

Ans: log₁₀3 + log ₁₀2 – 2log₁₀5 = log₁₀(6/25)

Example 04:

• Simplify log 5 + log 3 – Log2

Solution:

log 5 + Log 3 – Log2

= log ((5 x 3)/2) (Law of product and quotient)

= log (15/2)

Ans: log 5 + Log 3 – Log2 = log (15/2)

Example 05:

• Simplify ½ log 9 + 1/3 log 27

Solution:

½ log 9 + 1/3 log 27

=  log 9^½ + log 27^1/3(Law of exponent)

=  log 3 + log 3

= 2 log 3

= log 3² (Law of exponent)

= log 9

Ans: ½ log 9 + 1/3 log 27 = log 9

Example 06:

• Simplify 2 log₁₀4 – ½ log₁₀16 + 1

Solution:

2 log₁₀4 – ½ log₁₀16 + 1

= log₁₀4² – log₁₀16^½ + log₁₀10 (Law of exponent)

= log₁₀16 – log₁₀4 + log₁₀10

= log₁₀((16 x 10)/4) (Law of product and quotient)

= log₁₀ (40)

Ans: 2 log₁₀4 – ½ log₁₀16 + 1 = log₁₀ (40)

Example 07:

Simplify 2log3 – ½ log 16 + log 12

Solution:

2log3 –  ½ log 16 + log 12

= log3² – log 16^½ + log 12 (Law of exponent)

= log9 – log 4 + log 12

= log ((9 x 12)/4) (Law of product and quotient)

= log (9 x 3)

= log 27

Ans: 2log3 –  ½ log 16 + log 12 = log 27

Example 08:

Simplify ½ log₅36 + 2log₅7 – ½ log ₅12

Solution:

½ log₅36 + 2log₅7 – ½ log ₅12

= log₅36^½ + log₅7² –log ₅12^½ (Law of exponent)

= log₅6 + log₅49 –log ₅2√3

= log₅((6 x 49)/ 2√3) (Law of product and quotient)

= log₅((3 x 49)/ √3)

= log₅((√3 x √3 x 49)/ √3)

= log₅(49√3)

Ans: ½ log₅36 + 2log₅7 – ½ log ₅12 = log₅(49√3)

Example 09:

• Simplify 2 log 3 + 3 log 2

Solution:

2 log 3 + 3 log 2

= log 3² + log 2³ (Law of exponent)

= log 9 + log 8

= log (9 x 8) (Law of product)

= log 72

Ans: 2 log 3 + 3 log 2 = log 72

Example 10:

• Simplify 2 log 5 + 3 log 4 – 4 log 2

Solution:

2 log 5 + 3 log 4 – 4 log 2

= log 5² + log 4³ – log 2⁴ (Law of exponent)

= log 25 + log 64 – log 16

= log ((25 x 64)/16) (Law of product and quotient)

= log (25 x 4)

= log 100

Ans: 2 log 5 + 3 log 4 – 4 log 2 = log 100

Example 11:

• Simplify log₁₀2 + 3

Solution:

log₁₀2 + 3

= log₁₀2 + 3 x 1

= log₁₀2 + 3 x log₁₀10 (Number and base same rule)

= log₁₀2 + log₁₀10³ (Law of exponent)

= log₁₀2 + log₁₀1000

= log₁₀(2 x 1000) (Law of product)

= log₁₀(2000)

Ans: log₁₀2 + 3 = log₁₀(2000)

Example 12:

• Simplify log (x² – 3x + 2) – log (x – 1) + log (x – 2)

Solution:

log (x² – 3x + 2) – log (x – 1) + log (x – 2)

= log (x – 2)(x – 1) – log (x – 1) + log (x – 2)

= log ((x – 2)(x – 1)(x – 2))/(x – 1)) (Law of product and quotient)

= log (x – 2)(x – 2)

= log (x – 2)²

= 2 log (x – 2) (Law of exponent)

Ans: log (x² – 3x + 2) – log (x – 1) + log (x – 2) = log (x – 2)²

Example 13:

Simplify

Solution:

Example 14:

Simplify

Solution:

Example 15:

Simplify

Solution:

Example 16:

Simplify

Solution:

Example 17:

Simplify

Solution:

Example 18:

Simplify

Solution:

Example 19:

Simplify

Solution:

Example 20:

Simplify

Solution:

Example 21:

Simplify

Solution:

Example 22:

Simplify

Solution:

Example 23:

Simplify

Solution:

In the next article, we shall study to solve more problems on the laws of logarithms to prove given logarithmic expression.

Click Here for More Subtopics in Logarithms

Click Here for More Topics in Mathematics