Laws of Logarithms

Science > Mathematics > Algebra > Logarithms > Laws of Logarithm

In this article, we shall study the laws of logarithm and their proofs. Laws of logarithm are very important in mathematics and every student should have confidence in using them.

Laws of Product:

log_a(mn) = log_am + log_an, where a, m, n are positive real numbers with a ≠ 1

Proof:

Let log_am = x and log_an = y   ……. (1)

By the definition of logarithm, we have

a^x = m and a^y = n

Now mn = a^x . a^y

mn = a^{x + y}

By definition of logarithm

log_a (mn) = x + y

Substituting values of x and y from relation (1) we get

log_a (mn) = log_am + log_an (Proved)

Corollary:

log_a(mnp) = log_am + log_an + log_ap

Proof:

L.H.S. =  log_a (mnp)

∴ L.H.S. = log_a (mn) + log_a (p)  (Law of product)

∴ L.H.S. = log_a m + log_a n + log_a p  (Law of product)

log_a(mnp) = log_am + log_an + log_ap (Proved)

Law of Quotient:

log_a(m/n) = log_am – log_an, where a, m, n are positive real numbers with a ≠ 1, n ≠ 0

Proof:

Let log_am = x and log_an = y   ……. (1)

By the definition of logarithm, we have

a^x = m and a^y = n

Now m/n = a^x / a^y

m/n = a^{x – y}

By definition of logarithm

log_a (m/n) = x – y

Substituting values of x and y from relation (1) we get

log_a (m/n) = log_am – log_an (Proved)

Corollary:

log_a(mn/pq) = log_am + log_an – log_ap – log_aq

Proof:

L.H.S. = log_a(mn/pq)

∴ L.H.S. = log_a(mn) – log_a(pq)   (Law of quotient)

∴ L.H.S. = (log_am + log_an) – (log_ap + log_aq)  (Law of product)

∴ L.H.S. = log_am + log_an – log_ap – log_aq

log_a(mn/pq) = log_am + log_an – log_ap – log_aq (Proved)

Law of Exponent:

log_amⁿ = n. log_am where a, m, n are positive real numbers with a ≠ 1

Proof:

Let log_am = x     ……. (1)

By the definition of logarithm, we have

a^x = m

mⁿ = (a^x)ⁿ = a^nx

By definition of logarithm

log_amⁿ  = n x

Substituting value of x from relation (1) we get

log_amⁿ  = n log_am  (Proved)

Corollary:

log_a(x^py^q/z^rw^s) = (p log_ax + q log_ay) – (r log_az + s log_aw)

Proof:

L.H.S. = log_a(x^py^q/z^rw^s)

∴ L.H.S. = log_a(x^py^q) – log_a(z^rw^s)  (Law of quotient)

∴ L.H.S. = (log_ax^p + log_ay^q) – (log_az^r + log_aw^s)  (Law of product)

∴ L.H.S. = (p log_ax + q log_ay) – (r log_az + s log_aw)  (Law of exponent)

∴ L.H.S. = p log_ax + q log_ay – r log_az – s log_aw 

log_a(x^py^q/z^rw^s) = (p log_ax + q log_ay) – (r log_az + s log_aw) (Proved)

Logarithm of 1 to Any Base

Log_a1 = 0 i.e. Logarithm to any base is always zero.

Proof:

Let log_a1 = x ………. (1)

By definition of logarithm

a^x = 1

a^x = a⁰

x = 0

Substituting this value in equation (1) we get

log_a1 = 0 (Proved)

Logarithm of Any Number to the Same Base:

log_aa = 1 i.e. Logarithm of any number to the same base is 1

Proof:

Let log_aa = x ………. (1)

By definition of logarithm

a^x = a

a^x = a¹

x = 1

Substituting this value in equation (1) we get

log_aa = 1 (Proved)

Important Property:

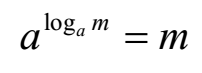
where a and m are positive real numbers with a ≠ 1

Proof:

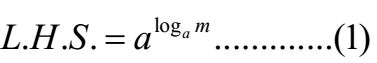
Let log _am = x

By definition of logarithm

a^x = m

Substituting in equation (1)

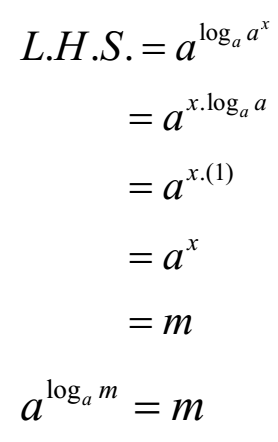
(Proved)

Change of Base Law:

where a, b, and m are positive real numbers with a ≠ 1 and b ≠ 1

Proof:

Let log_am = x, log_bm = y and log_ba = z    ……. (1)

By the definition of logarithm, we have

a^x = m  ……….. (2)

b^y = m  ……….. (3)

b^z = a  ……….. (4)

From equations (2) and (3)

a^x = b^y    ……….. (5)

Substituting value of a from equation (4) in (5) we get

(b^z)^x = b^y

b^zx = b^y

zx = y

x = y/z

Substituting the values of x, y, and z from equation (1) we get

(Proved)

Corollary:

Proof:

We have

Substitute m = b

(Proved)

In the next few articles, we shall study how to use the laws of logarithm to evaluate or simplify given logarithmic expression.

Click Here for More Subtopics in Logarithms

Click Here for More Topics in Mathematics