Use of the Laws of Logarithms: Set – V

Science > Mathematics > Algebra > Logarithms > Use of Laws of Logarithms Set – V (Change of Base Rule)

In the next article, we shall study to solve more problems on the laws of logarithms to prove given logarithmic relation. In this article, we shall study problems based on the change of base rule.

Laws of Logarithms

• Log a + Log b = Log (ab) (Law of Product)
• Log a – log b = log (a/b)    b ≠ 0 (law of Quotient)
• Log a^m = m Log a (Law of exponent)
• Log (1) = 0
• Log_aa = 1
• 
• 
• 

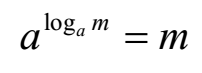
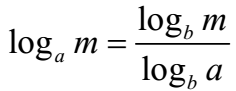
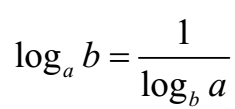
Change of Base Rule

Example 01:

Show that

Solution:

(Proved as required)

Example 02:

Show that

Log_ab . log_bc . log_cd = log_ad

Solution:

Log_ab . log_bc . log_cd = log_ad 

(Proved as required)

Example 03:

Show that

Log_ba . log_cb . log_ac = 1

Solution:

Log_ba . log_cb . log_ac = 1

(Proved as required)

Example 04:

Show that

Solution:

(Proved as required)

Example 05:

Show that

Solution:

(Proved as required)

Example 06:

Show that

Solution:

(Proved as required)

Example 07:

Show that

Solution:

(Proved as required)

Example 08:

Show that

Solution:

(Proved as required)

Example 09:

Show that

Solution:

(Proved as required)

Example 10:

Show that

Solution:

(Proved as required)

Example 11:

Show that

Solution:

(Proved as required)

Example 12:

Show that

Solution:

(Proved as required)

Example 13:

Show that

Solution:

(Proved as required)

Example 14:

Show that

Solution:

(Proved as required)

Example 15:

Show that

Solution:

In the next article, we shall study to solve problems on the laws of the logarithm to find the value of x.

Click Here for More Subtopics in Logarithms

Click Here for More Topics in Mathematics