Logarithms

In this article, we shall study to solve problems on logarithms in which a relation is given using which we have to prove another relation.

Laws of Logarithms

• Log a + Log b = Log (ab) (Law of Product)
• Log a – log b = log (a/b)    b ≠ 0 (law of Quotient)
• Log a^m = m Log a (Law of exponent)
• Log (1) = 0
• Log_aa = 1
• 
• 
• 

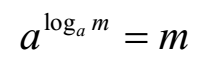
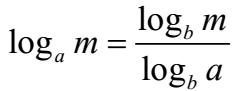
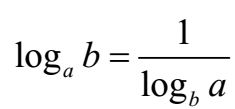
Example 01:

If , then Show that abc = 1

Solution:

Given

∴Log a = k(y – z) ……………. (1)

∴ Log b = k(z – x) ……………. (2)

∴ Log c = k(x – y) ……………. (3)

Adding equations (1), (2) and (3)

Log a+ Log b + Log c  = k(y – z) + k(z – x) + k(x – y)

∴ Log (abc) = k(y – z + z – x + x – y)

∴ Log (abc) = 0

∴ Log (abc) = log (1)

∴ abc = 1

(Proved as required)

Example 02:

If , then Show that a^xb^yc^z = 1

Solution:

Given

∴ Log a^x = k(xy – xz) ……………. (1)

∴ Log b^y = k(yz – xy) ……………. (2)

∴ Log c^z = k(xz – yz) ……………. (3)

Adding equations (1), (2) and (3)

Log a^x + Log b^y + Log c^z  = k(xy – xz) + k(yz – xy) + k(xz – yz)

∴ Log (a^x b^y c^z ) = k(xy – xz + yz – xy + xz – yz)

∴Log (a^x b^y c^z ) = 0

∴ Log (a^x b^y c^z ) = log (1)

∴ a^x b^y c^z = 1

(Proved as required)

Example 03:

If , then Show that a^{y + z}b^{z + x}c^{x + y} = 1

Solution:

Given

∴ Log a^y+z = k(y² – z²) ……………. (1)

∴ Log b^z+x = k(z² – x²) ……………. (2)

∴Log c^x+y = k(x² – y²) ……………. (3)

Adding equations (1), (2) and (3)

Log a^y+z + Log b^z+x + Log c^x+y  = k(y² – z²) + k(z² – x²) + k(x² – y²)

∴ Log (a^y+z b^z+x c^x+y) = k(y² – z² + z² – x² + x² – y²)

∴ Log (a^y+z b^z+x c^x+y) = 0

∴ Log (a^y+z b^z+x c^x+y) = log (1)

∴ a^y+z b^z+x c^x+y = 1

(Proved as required)

Example 04:

If then Show that xyz = 1

Solution:

Given

∴ Log x = k(ab – ac) ……………. (1)

∴ Log y = k(bc – ab) ……………. (2)

∴ Log z = k(ac – bc) ……………. (3)

Adding equations (1), (2) and (3)

Log x + Log y + Log z  = k(ab – ac) + k(bc – ab) + k(ac – bc)

∴ Log (xyz) = k(ab – ac + bc – ab + ac – bc)

∴ Log (xyz) = 0

∴ Log (xyz ) = log (1)

∴ xyz= 1

(Proved as required)

Example 05:

If Show that abc = 1

Solution:

Given

∴ Log a= k(x + y – 2z) ……………. (1)

∴ Log b = k(y + z – 2x) ……………. (2)

∴ Log c= k(z + x -2y) ……………. (3)

Adding equations (1), (2) and (3)

Log a + Log b + Log c= k(x + y – 2z) + k(y + z – 2x) + k(z + x -2y)

∴ Log (abc) = k(x + y – 2z + y + z – 2x + z + x -2y)

∴ Log (abc) = 0

∴ Log (abc) = log (1)

∴ abc = 1

(Proved as required)

Example 06:

If and a³b²c = 1, find value of k

Solution:

Given

∴ Log₂a³ = 12x ……………. (1)

∴ Log₂b² = 12x ……………. (2)

∴ Log₂c= 3kx ……………. (3)

Adding equations (1), (2) and (3)

Log₂a³ + Log₂b² + Log₂c  = 12x + 12x + 3kx

∴ Log₂ (a³ b²c) = 24x + 3kx

∴ Log₂ (1) = x(24 + 3k)

∴ 0 = x(24 + 3k)

∴ 24 + 3k = 0

∴ 3k = – 24

∴ K = – 8

Example 07:

If and a⁴b³c^-2 = 1, find value of x

Solution:

Given

∴ Loga⁴ = 4kx ……………. (1)

∴ Logb³ = 6k ……………. (2)

∴ Logc^-2=  – 10k ……………. (3)

Adding equations (1), (2) and (3)

Loga⁴ + Logb³ + Logc^-2  = 4kx + 6k – 10k

∴ Log(a⁴b³c^-2) = k(4x + 6 – 10)

∴ Log₂ (1) = = k(4x  – 4)

∴ 0 = k(4x  – 4)

∴ 4x – 4 = 0

∴ 4x = 4

∴ x = 1

Example 08:

If a² = b³ = c⁵ = d⁶, then show that log_dabc = 31/5

Solution:

Given

a² = b³ = c⁵ = d⁶

∴ a = d^6/2 = d³

∴ b = d^6/3 = d²

∴ c = d^6/5

∴ L.H.S. = log_dabc

∴ L.H.S. = log_d(d³ d² d^6/5)

∴ L.H.S. = log_d(d^31/5)

∴ L.H.S. = (31/5) log_dd

∴ L.H.S. = (31/5)(1)

∴ L.H.S. = 31/5

(Proved as required)

Example 09:

If a² = b³ = c⁴ = d⁵, then show that log_abcd = 47/30

Solution:

Given

a² = b³ = c⁴ = d⁵

∴ b = a^2/3

∴ c = a^2/4 = d^1/2

∴ d = a^2/5

∴ L.H.S. = log_abcd

∴ L.H.S. = log_a(a^2/3  a^1/2 a^2/5)

∴ L.H.S. = log_a(d^47/30)

∴ L.H.S. = (47/30) log_aa

∴ L.H.S. = (47/30)(1)

∴ L.H.S. = 47/30

(Proved as required)