In the previous articles, we have studied the basics of set theory and its terminology. In this article, we shall study operations of sets including Union of sets, Intersection of sets, a complement of a set, Cartesian product of sets.
The basic operations on sets are:
- Union of sets
- Intersection of sets
- A complement of a set
- Set difference
- Cartesian product of sets.
Union of Sets:
If A and B are two sets, the union of A and B (written as A ∪ B) the set of all objects which either belong to A or to B or to both of them.
A ∪ B = {x|x ∈ A or x ∈ B]
Venn Diagram for Union of Sets:
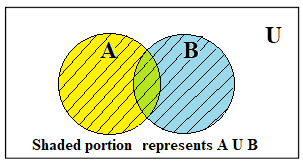
Example:
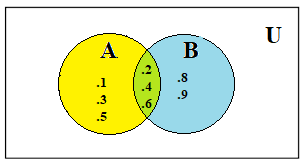
If A {1, 2, 3, 4, 5, 6} and B {2, 4, 6, 8, 9}
then A ∪ B {1, 2, 4, 5, 6, 8, 9}.
Here the elements 2, 4, and 6, which belong to both sets, are written only once. We can show A ∪ B by a Venn Diagram as follows:
Properties of Union of Sets:
Commutative Property of Union of Sets:
The Commutative Property for Union says that the order of the sets in which we do the operation does not change the result. Thus if A and B are two sets, then
A ∪ B = B ∪ A
Example:
Let A = {x : x is a whole number between 4 and 8} and
B = {x : x is an even natural number less than 10}.
A = {5, 6, 7}, B = {2, 4, 6, 8}
A ∪ B = {5, 6, 7} ∪ {2, 4, 6, 8} = {2, 4, 5, 6, 7, 8} ……….. (1)
B ∪ A = {2, 4, 6, 8} ∪ {5, 6, 7} = {2, 4, 5, 6, 7, 8} ……….. (2)
From (1) and (2) we get
A ∪ B = B ∪ A
Associative Property of Union of Sets:
The Associative Property for Union says that how the sets are grouped does not change the result. Thus, if A, B, and C are three sets, then
A ∪ (B ∪ C) = (A ∪ B) ∪ C
Example:
Let A = {x | x is a whole number between 4 and 8} and
B = {x | x is an even natural number less than 10}.
C = {x | x is an odd natural number less than 10}.
A = {5, 6, 7}, B = {2, 4, 6, 8}, C = {1, 3, 5, 7, 9}
A ∪ (B ∪ C) = {5, 6, 7} ∪ [ {2, 4, 6, 8} ∪ {1, 3, 5, 7, 9}]
A ∪ (B ∪ C) = {5, 6, 7} ∪ {1, 2, 3, 4, 5, 6, 7, 8, 9}
A ∪ (B ∪ C) = {1, 2, 3, 4, 5, 6, 7, 8, 9} ……….. (1)
(A ∪ B) ∪ C = [{5, 6, 7} ∪ {2, 4, 6, 8}] ∪ {1, 3, 5, 7, 9}
(A ∪ B) ∪ C = {2, 4, 5, 6, 7, 8} ∪ {1, 3, 5, 7, 9}
(A ∪ B) ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9} ……….. (2)
From (1) and (2) we get
A ∪ (B ∪ C) = (A ∪ B) ∪ C
Identity Property for Union:
The Identity Property for Union says that the union of a set and the empty set is the set itself. Thus, if A is a set, then
A ∪ ∅ = ∅ ∪ A = A
Example:
Let A = {3, 7, 11} and
B = {x | x is a natural number less than 0}.
B = {}
Then A ∪ B = {3, 7, 11} ∪ { } = {3, 7, 11} = A
The empty set is the identity element for the union of sets.
Intersection of Sets:
If A and B are two sets, the intersection of A and B (written as A ∩ B) the set of all objects which belong to A and to B.
A ∩ B = {x|x ∈ A and x ∈ B}
Venn Diagram for Intersection of Sets:

Example:
If A {1, 2, 3, 4, 5, 6} and B {2, 4, 6, 8, 9}
then A ∩ B {2, 4, 6}.
We can show A ∩ B by a Venn Diagram as follows:

Properties of Intersection of Sets:
Commutative Property of Intersection of Sets:
The Commutative Property for Intersection says that the order of the sets in which we do the operation does not change the result. Thus if A and B are two sets, then
A ∩ B = B ∩ A
Example:
Let A = {x : x is a whole number between 4 and 8} and
B = {x : x is an even natural number less than 10}.
A = {5, 6, 7}, B = {2, 4, 6, 8}
A ∩ B = {5, 6, 7} ∪ {2, 4, 6, 8} = {6} ……….. (1)
B ∩ A = {2, 4, 6, 8} ∪ {5, 6, 7} = {6} ……….. (2)
From (1) and (2) we get
A ∩ B = B ∩ A
Associative Property of Intersection of Sets:
The Associative Property for Union says that how the sets are grouped does not change the result. Thus, if A, B, and C are three sets, then
A ∩ (B ∩ C) = (A ∩ B) ∩ C
Example:
Let A = {x | x is a whole number between 4 and 8} and
B = {x | x is an even natural number less than 10}.
C = {x | x is 3 multiple natural number less than 10}.
A = {5, 6, 7}, B = {2, 4, 6, 8}, C = {3, 6, 9}
A ∩ (B ∩ C) = {5, 6, 7} ∩ [ {2, 4, 6, 8} ∩ {3, 6, 9}]
A ∩ (B ∩ C) = {5, 6, 7} ∩ {6} = {6} ……….. (1)
A ∩ (B ∩ C) = [{5, 6, 7} ∩ {2, 4, 6, 8}] ∩ {3, 6, 9}
A ∩ (B ∩ C) = {6} ∩ {3, 6, 9} = {6} ……….. (2)
From (1) and (2) we get
A ∩ (B ∩ C) = (A ∩ B) ∩ C
Identity Property for Intersection:
The Identity Property for Intersection says that the intersection of a set and the empty set is an empty set. Thus, if A is a set, then
A ∩ ∅ = ∅ ∩ A = ∅
Example:
Let A = {3, 7, 11} and
B = {x | x is a natural number less than 0}.
B = {}
Then A ∩ B = {3, 7, 11} ∩ { } = { }
Distributive Properties:
Distributive Property of Union over Intersection:
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Example:
Let A = {a, n, t}, B = {t, a, p}, and C = {s, a, p}
A ∪ (B ∩ C) = {a, n, t} ∪ [{t, a, p} ∩ {s, a, p}]
A ∪ (B ∩ C) = {a, n, t} ∪ {a, p} = {p, a, n, t} ……….. (1)
(A ∪ B) ∩ (A ∪ C) = [{a, n, t} ∪ {t, a, p}] ∩ [{a, n, t} ∪ {s, a, p}]
(A ∪ B) ∩ (A ∪ C) = {a, n, t, p} ∩ {a, n, t, p, s}
(A ∪ B) ∩ (A ∪ C) = {p, a, n, t} ……….. (2)
From (1) and (2)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Distributive Property of Intersection over Union:
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Example:
Let A = {a, n, t}, B = {t, a, p}, and C = {s, a, p}
A ∩ (B ∪ C) = {a, n, t} ∩ [{t, a, p} ∪ {s, a, p}]
A ∩ (B ∪ C) = {a, n, t} ∩ {t, a, p, s} = {a, t} ……….. (1)
(A ∩ B) ∪ (A ∩ C) = [{a, n, t} ∩ {t, a, p}] ∪ [{a, n, t} ∩ {s, a, p}]
(A ∩ B) ∪ (A ∩ C) = {a, t} ∪ {a}
(A ∩ B) ∪ (A ∩ C) = {a, t} ……….. (2)
From (1) and (2)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Complement of a Set:
Concept of Universal Set:
Whenever a number of sets A, B, C …. are under consideration, they are being thought of as subsets of some set X. Such a set X is called universal set.
For example, if A {1, 2, 3, 4, 5}, B {1, 5, 9, 12, 17} and C {1, 2, 3, ….100} are sets under consideration, we can think of A, B, C as being subsets of the universal set N of natural numbers.
Complement of a Set:
Suppose A is a set which is the subset of a universal set X or U. Then the set of all the elements of X which do not belong to A is called the complement of A with respect to X and is denoted as A’ or Ac or X – A.
In the set builder notation: A’ = {x| x ∉ X and x ∈A}, where A is a subset of the universal set X.
For example, if N is the universal set and
A = {2x| x ∈ N}i.e. A = {2, 4, 6, 8 …},
Then A’ ={1, 3, 5, 7, 9 ….} or A’ = {(2x-1)|x ∈ N}
A Venn diagram showing A’ is given in the figure. Here X is the universal set and the shaded portion represents A’.

In a Venn diagram showing complements, it is customary (though not compulsory) to draw the universal set X using a rectangle or square and the sets A, B, C, …. using circles or triangles.
Properties of Complement of a Set:
Complement law:
The union of a set A and its complement A’ gives the universal set U of which, A and A’ are a subset. i.e. A ∪ A’ = U
Example:
If A = {1 , 2 , 3 } and X = {1 , 2 , 3 , 4 , 5, 6 }, then A’ = {4 , 5, 6}.
Now, A ∪ A’ = { 1 , 2 , 3 , 4 , 5} = U
Disjoint Law:
A set and its complement, are disjoint sets or the intersection of a set A and its complement A’ gives the empty set ∅. i.e. A ∩ A’ = ∅
Example:
If A = {1 , 2 , 3 } and X = {1 , 2 , 3 , 4 , 5, 6 }, then A’ = {4 , 5, 6}.
Now, A ∩ A’ = { } = ∅
Law of Double Complementation:
If we take the complement of the complemented set A’ then, we get the set A itself. i.e. (A’)’ = A
Example:
If A = {1 , 2 , 3 } and X = {1 , 2 , 3 , 4 , 5, 6 }, then A’ = {4 , 5, 6}
Now, (A’)’ = {1 , 2 , 3 } = A
Complement of Empty Set:
The complement of an empty set gives us a universal set.
If X = {1 , 2 , 3 , 4 , 5, 6 }, then ∅’ = {1 , 2 , 3 , 4 , 5, 6 } = X
Complement of Universal Set:
The complement of the universal set gives us the empty set.
Example:
If X = {1 , 2 , 3 , 4 , 5, 6 }, then X’ = { } = ∅
Demorgan’s law (I):
(A ∪ B)’ = A’ ∩ B’ (De Morgan’s law)
Example:
If A = {1 , 2 , 3, 7 }, B = {2, 4, 6} and X = {1 , 2 , 3 , 4 , 5, 6, 7 },
then A’ = {4 , 5, 6} and B’ = {1, 3, 5, 7}
A ∪ B = {1 , 2 , 3, 7 } ∪ {2, 4, 6} = {1, 2, 3, 4, 6, 7}
(A ∪ B)’ = {5} …………. (1)
A’ ∩ B’ = {4 , 5, 6} ∩ {1, 3, 5, 7} = {5} …………….. (2)
From (1) and (2)
(A ∪ B)’ = A’ ∩ B’
Demorgan’s law (II):
(A ∩ B)’ = A’ ∪ B’ (De Morgan’s law)
Example:
If A = {1 , 2 , 3, 7 }, B = {2, 4, 6} and X = {1 , 2 , 3 , 4 , 5, 6, 7 },
then A’ = {4 , 5, 6} and B’ = {1, 3, 5, 7}
A ∩ B = {1 , 2 , 3, 7 } ∩ {2, 4, 6} = {2}
(A ∩ B)’ = {1, 3, 4, 5, 6, 7} …………. (1)
A’ ∪ B’ = {4 , 5, 6} ∪ {1, 3, 5, 7} = {1, 3, 4, 5, 6, 7} …………….. (2)
From (1) and (2)
(A ∩ B)’ = A’ ∪ B’
Summary of Results:
- A ∪ A’ = A’ ∪ A = ∪ (Complement law)
- (A ∩ A’) = ϕ (Complement law)
- (A’)’ = A (Law of complementation)
- (ϕ’ = ∪ (Complement of empty set)
- ∪’ = ϕ (Complement of universal set)
- (A ∪ B) = A’ ∩ B’ (De Morgan’s law)
- (A ∩ B)’ = A’ ∪ B’ (De Morgan’s law)
Difference of Sets:
If A and B are two sets, then the difference of two sets A and B is equal to the set which consists of elements present in A but not in B. It is represented by A – B.
The difference of sets (A – B) is represented by the Venn diagram as follows:

Example:
If A = {1, 2, 3, 4, 5, 6, 7} and B = {5, 6, 7} are two sets.
Then, the difference of set A and set B is given by;
A – B = {1, 2, 3, 4}
Properties of Difference of Sets:
The difference of set A and set B is equal to the intersection of set A with the complement of set B. i.e. A − B = A ∩ B’
Example:
If A = {1,2, 5,6,7}, B = {5, 6, 7} and universal set X = {1, 2, 3, 4, 5, 6, 7, 8}
Then, the difference of set A and set B is given by;
A – B = {1,2} …………….. (1)
A ∩ B’ = {1,2, 5,6,7} ∩ {1, 2, 3, 4, 8} = {1, 2} ……….. (2)
From (1) and (2)
A − B = A ∩ B’
Cartesian Product:
Ordered Pair:
In Coordinate Geometry, when we say that a point has a coordinates (4, 5), it means that its x coordinate is 4 and y coordinate is 5.The pair of numbers 4 and 5 is written in a definite order in a bracket. Such a representation is an ordered pair. The ordered pair (5, 4) is different from the ordered pair (4, 5) as the order of the two elements is changed.
Hence in general, an ordered pair (x, y) represents two objects x and y which must be taken in that order.
Two ordered pairs (x, y) and (a, b) are equal if and only if x = a and y = b.
Cartesian Product of Sets:
The Cartesian product of two non-empty sets A and B is denoted by A×B and defined as the “collection of all the ordered pairs (a, b) such that a ∈ A and b ∈ B. a is called the first element and b is called the second element of the ordered pair (a, b).
A×B = {(a, b) : a ∈ A, b ∈ B}
Example 1:
If A = {a, b, c} and B = {1, 2}, then
A × B = {a, b, c} × {1, 2}
A × B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}.
We note that since A has 3 elements (which is written as n(A) = 3) and B has two elements (which is written as n(B) =2). A x B has 3 x 2 = 6 elements, or n(A x B) = 6.
Example 2:
If A = {a, b, c}, then
A × A = {a, b, c} × {a, b, c}
A × A = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)}.
Example 3:
R set of Real numbers. Hence R x R represents all possible ordered pairs of real numbers which are the coordinates of all points on the usual geometric plane. Hence R x R, (which is also written as R2) represents the usual coordinate plane.