Problems Based on Definition of Logarithm

Science > Mathematics > Algebra > Logarithms > Problems Based on Definition of Logarithms

In the last article, we have studied the concept of logarithm and interconversion between exponential form and logarithmic form. In this article, we shall study to solve problems based on the definition of logarithm.

Definition of Logarithm:

If m = a^x, where a > 0 and m > 0 then x is called the logarithm of m to the base a and is written as x = log_am and read as a log of m to the base a where m, a, x are real numbers.

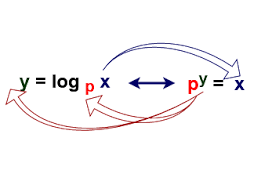
Note the change in position of the terms during conversion from one form to another.

Example 01:

• Find the value of log₂32

Solution:

Let log₂32 = x

By definition of logarithm

∴ 2^x = 32

∴ 2^x = 2⁵

∴ x = 5

Ans: log₂32 = 5

Example 02:

• Find the value of log₁₀100000

Solution:

Let log₁₀100000 = x

By definition of logarithm

∴ 10^x = 100000

∴ 10^x = 10⁵

∴ x = 5

Ans: log₁₀100000 = 5

Example 03:

• Find the value of log₅3125

Solution:

Let log₅3125 = x

By definition of logarithm

∴ 5^x= 3125

∴ 5^x = 5⁵

∴ x = 5

Ans: log₅3125 = 5

Example 04:

• Find the value of log₅125

Solution:

Let log₅125 = x

By definition of logarithm

∴ 5^x = 125

∴ 5^x = 5³

∴ x = 3

Ans: log₅125 = 3

Example 05:

Find the value of log _1/2  8

Solution:

Let  log _1/2  8  = x

By definition of logarithm

∴ (1/2)^x = 8

∴ (2^-1)^x = 2³

∴ 2^-x = 2³

∴ -x = 3

∴ x = -3

Ans: log _1/2  8 = -3

Example 06:

• Find the value of log₈16

Solution:

Let log₈16 = x

By definition of logarithm

∴ (8)^x = 16

∴(2³)^x = 2⁴

∴ 2^3x = 2⁴

∴ 3x = 4

∴ x = 4/3

Ans: log₈16 = 4/3

Example 07:

• Find the value of log₆₄4

Solution:

Let log₆₄4 = x

By definition of logarithm

∴ 64^x = 4

∴ (2⁶)^x = 2²

∴ 2^6x = 2²

∴ 6x = 2

∴ x = 1/3

Ans: log₆₄4 = 1/3

Example 08:

• Find the value of log₁₆32

Solution:

Let log₁₆32 = x

By definition of logarithm

∴ 16^x = 32

∴ (2⁴)^x = 2⁵

∴ 2^4x = 2⁵

∴ 4x = 5

∴ x = 5/4

Ans: log₁₆32 = 5/4

Example 09:

• Find the value of log₉(1/81)

Solution:

Let Log₉(1/81) = x

By definition of logarithm

∴ 9^x = 1/81

∴ (3²)^x = 1/3⁴

∴ 3^2x = 3^-4

∴ 2x = -4

 ∴ x = -2

Ans: log₉(1/81) = -2

Example 10:

• Find the value of log₂(1/256)

Solution:

Let Log₂(1/256) = x

By definition of logarithm

∴ 1/256 = 2^x

∴ 1/2⁸ = 2^x

∴ 2^-8 = 2^x

∴ x = -8

Ans: log₂(1/256) = -8

Example 11:

• Find the value of log₈₁ 27

Solution:

Let log₈₁ 27 = x

By definition of logarithm

∴ 81^x = 27

∴ (3⁴)^x = 3³

∴ 3^4x = 3³

∴ 4x = 3

∴ x = ¾

Ans: log₈₁ 27 = 3/4

Example 12:

• Find the value of log₁₀0.001

Solution:

Let log₁₀0.001 = x

By definition of logarithm

∴ 10^x = 0.001

∴ 10 ^x = 1/1000

∴ 10 ^x = 1/10³

∴ 10 ^x = 10^-3

∴ x = -3

Ans: log₁₀0.001 = – 3

Example 13:

• Find the value of log₅0.008

Solution:

Let log₅0.008 = x

By definition of logarithm

∴ 5^x = 0.008

∴ 5^x = 8/1000

∴ 5^x = 1/125

∴ 5^x = 1/5³

∴ 5^x = 5^-3

∴ x = -3

Ans: log₅0.008 = -3

Example 14:

• Find the value of

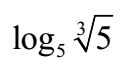
Solution:

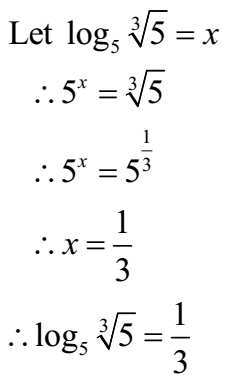
Example 15:

• Find the value of

Solution:

Example 16:

• Find the value of

Solution:

Example 17:

• Find the value of

Solution:

Example 18:

• Find the value of

Solution:

Example 19:

• Find the value of

Solution:

Example 20:

• Find the value of log₂(log_xx²)

Solution:

Log₂(log_xx²) = Log₂(2log_xx) = Log₂(2(1))

= Log₂2 = 1

Ans: Log₂(log_xx²)  = 1

Example 21:

• Find the value of log₅(log_xx²)

Solution:

Log₂(log₃3) = Log₅(1) = 0

Ans: Log₅(log_xx²) = 0

Example 22:

Find the value of

Solution:

Example 23:

Find the value of

Solution:

In the next article, we shall see laws of the logarithm, and problems based on them.

Click Here for More Subtopics in Logarithms

Click here for More Topics in Mathematics