Science > Mathematics > Algebra > Logarithms > Use of Laws of Logarithms Set – III
In the last article, we have studied to solve problems on the use of laws of logarithms to prove given logarithmic expression. In this article, we shall study to solve more problems on these laws to prove given relation using given logarithmic expression.
Example 01:
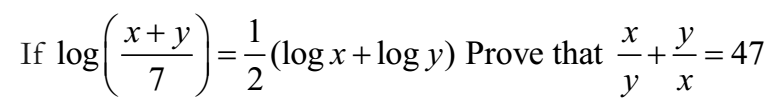
Solution:
Given
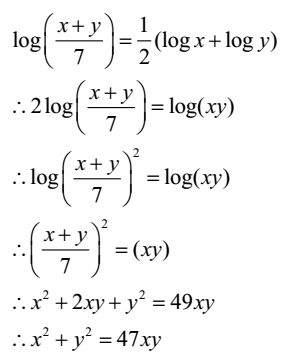
Dividing both sides by xy
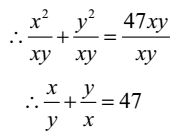
Proved as required.
Example 02:

Solution:
Given

Dividing both sides by xy

Proved as required.
Example 03:

Solution:
Given

Dividing both sides by xy

Proved as required.
Example 04:

Solution:
Given

Proved as required.
Example 05:

Solution:
Given

Proved as required.
Example 06:

Solution:
Given

Proved as required.
Example 07:

Solution:
Given

Proved as required.
Example 08:
Given 2log2(x + y) = 3 + log2x + log 2y, Show that x2 + y2 = 6xy
Solution:
Given 2log2(x + y) = 3 + log2x + log 2y
log2(x + y)2 = 3 log22 + log2x + log 2y
log2(x + y)2 = log223 + log2x + log 2y
log2(x + y)2 = log28 + log2x + log 2y
log2(x + y)2 = log28xy
(x + y)2 = 8xy
x2 + 2xy + y2 = 8xy
x2 + y2 = 6xy
Proved as required.
Example 09:
If a2 + b2 = 3ab, show that 
Solution:
a2 + b2 = 3ab
Adding 2ab on both sides
a2 + 2ab + b2 = 3ab + 2ab
(a + b)2 = 5ab

Proved as required.
Example 10:
If a2 -12ab+ 4b2 = 0, show that

Solution:
a2 -12ab+ 4b2 = 0
a2 + 4b2 = 12ab
Adding 4ab on both sides
a2 + 4ab + 4b2 = 12ab + 4ab
(a + 2b)2 = 16ab

Proved as required
Example 11:
If a2 + b2 = 7ab, show that 
Solution:
a2 + b2 = 7ab
Adding 2ab on both sides
a2 + 2ab + b2 = 7ab + 2ab
(a + b)2 = 9ab

Proved as required.
Example 12:
If b2 = ac, prove that log a + log c = 2 log b
Solution:
b2 = ac
Taking log on both sides
Log b2 = log (ac)
2 log b = log a +log c
Log a + log c = 2 log b
Proved as required.
In the next article, we shall study to solve more problems on these laws to prove given logarithmic relation.