Use of the Laws of Logarithms: Set – VI

Science > Mathematics > Algebra > Logarithms > Use of Laws of Logarithms Set – V (Solve for x)

In the last article, we shall study problems based on the change of base rule. In this article, we shall study the use of definition and the laws of logarithms to find the value of ‘x’ (solve for x).

Example 01:

Solve for x, if log₅x = 2

Solution:

Given: log₅x = 2

∴ x = 5² = 25

∴ x = 25

Example 02:

Solve for x, if log₂(1/2) = x

Solution:

Given: log₂(1/2) = x

∴ log₂2^-1 = x

∴ x = -1 Log22

∴ x = – 1(1)

∴ x = -1

Example 03:

Find x, if log₄(x – 2) = 2

Solution:

Given: log₄(x – 2) = 2

∴ x – 2 = 4²

∴ x – 2 = 16

∴ x = 18

Example 04:

Find x, if log₅(x² – 5x + 11) = 1

Solution:

Given: log₅(x² – 5x + 11) = 1

∴ x² – 5x + 11 = 5¹

∴ x² – 5x + 6 = 0

∴ (x – 3)(x – 2) = 0

∴ x – 3 = 0 or x – 2 = 0

∴ x = 3 or x = 2

Both x = 3 and x = 2 satisfy given relation

x = 3 or x = 2

 Example 05:

Find x, if log₂x – log₂(x – 1) = 5

Solution:

Given: Log₂x – log₂(x – 1) = 5

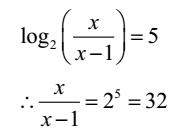
∴ x = 32x – 32

∴31x = 32

∴ x = 32/31

Example 06:

Find x, if log x + log(x + 1) = log 6

Solution:

Given: log x + log(x + 1) = log 6

∴ log x(x + 1) = log 6

∴x(x + 1) = 6

∴ x² + x – 6 = 0

∴ (x + 3)(x – 2) = 0

∴ x = -3 or x = 2

x = -3 is not possible because log of negative number not defined.

∴ x = 2

Example 07:

Find x, if log (1 + x) – log (1 – x) = 1

Solution:

Given: log (1 + x) – log (1 – x) = 1

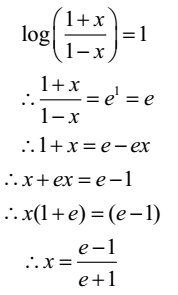
Example 08:

Find x, if log₃(x + 6) = 2

Solution:

Given: log₃(x + 6) = 2

∴ x + 6 = 3² = 9

∴ x = 3

Example 09:

Find x, if log (x + 3) + log (x – 3) = log 16, find x

Solution:

Given: log (x + 3) + log (x – 3) = log 16

∴ log [(x + 3)(x – 3)] = log 16

∴ log (x² – 3²) = log 16

∴ x² – 9 = 16

∴ x²  = 25

∴ x = ± 5

∴ x = -5 is not possible because the log of negative numbers not defined.

∴ x = 5

Example 10:

Find x, if log (3x + 2) + log (3x – 2) = log 5

Solution:

Given: log (3x + 2) + log (3x – 2) = log 5

∴ log [(3x + 2)(3x – 2)] = log 5

∴ log ((3x)² – 2²) = log 16

∴ 9x² – 4 = 5

∴ 9x²  = 9

∴ x²  = 1

∴ x = ± 1

x = -1 is not possible because log of negative number not defined.

∴  x = 1

Example 11:

Find x, if log (3x + 2) – log (3x – 2) = log 5

Solution:

Given: log (3x + 2) – log (3x – 2) = log 5

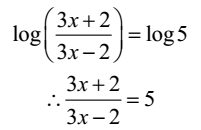
∴ 3x + 2 = 15x – 10

∴ 12 = 12x

∴x = 12/12 = 1

Example 12:

Find x, if

Solution:

Given:

∴ log(x + 6) = 2 log x

∴ log(x + 6) = log x²

∴ x + 6 = x²

∴ x² – x – 6 = 0

∴ (x – 3)(x + 2) = 0

∴ x – 3 = 0 and x + 2 = 0

∴ x = 3 or x = -2

x = -2 is not possible because log of negative number not defined.

∴ x = 3

Example 13:

Find x, if log₃x + log₃4 = 2

Solution:

Given: log₃x + log₃4 = 2

∴ log₃4x = 2

∴ 4x = 3² = 9

∴ x = 9/4

Example 14:

Find x, if log₂(x² + 7) = 4

Solution:

Given: log₂(x² + 7) = 4

∴ x² + 7 = 2⁴

∴ x² + 7 = 16

∴ x² = 9

∴ x = ±3

both x = 3 and x = -3 satisfy the given relation

∴ x = 3 and x = -3

Example 15:

Find x, if log₂x + log₂(x + 2) = 3

Solution:

Given: log₂x + log₂(x + 2) = 3

∴ log₂x(x + 2) = 3

∴ x(x + 2) = 2³

∴ x² + 2x = 8

∴ x² + 2x – 8 = 0

∴ (x + 4)(x – 2) = 0

∴  x + 4 = 0 or x – 2 = 0

∴ x = -4 and x = 2

x = -4 is not possible because the log of negative numbers not defined.

∴ x = 2

In the next article, we shall study to solve more problems on the laws of the logarithm to find the value of x.

Click Here for More Subtopics in Logarithms

Click Here for More Topics in Mathematics