Radius of curvature of the curve y = f(x) is given by
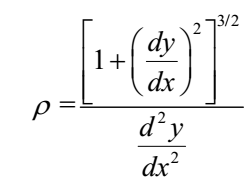
Example 01:
Find the radius of curvature of the curve y = x3 at (2, 8)
Solution:
Equation of curve is y = x3 ………. (1)
Differentiating both sides w.r.t. x
(dy/dx) = 3x2 ………………. (2)
(dy/dx) at P(2, 8) = 3(2)2 = 12
Differentiating equation (2) again w.r.t. x
d2y/dx2 = 6x
(d2y/dx2) at P(2, 8) = 6(2) = 12
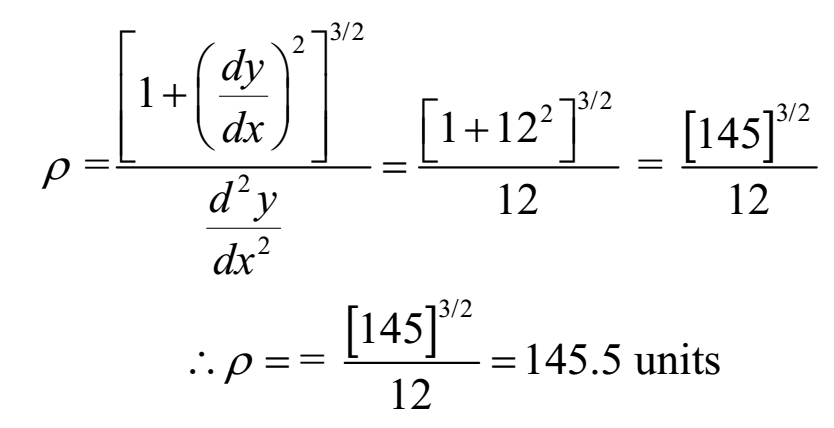
Ans: Radius of curvature of the given curve at (2, 8) is 145.5 units
Example 02:
Find the radius of curvature of the curve y = x3 at (1, 1)
Solution:
Equation of curve is y = x3 ………. (1)
Differentiating both sides w.r.t. x
(dy/dx) = 3x2 ………………. (2)
(dy/dx) at P(1,1) = 3(1)2 = 3
Differentiating equation (2) again w.r.t. x
(d2y/dx2) = 6x ………………. (2)
(d2y/dx2) at P(1,1) = 6(1) = 6
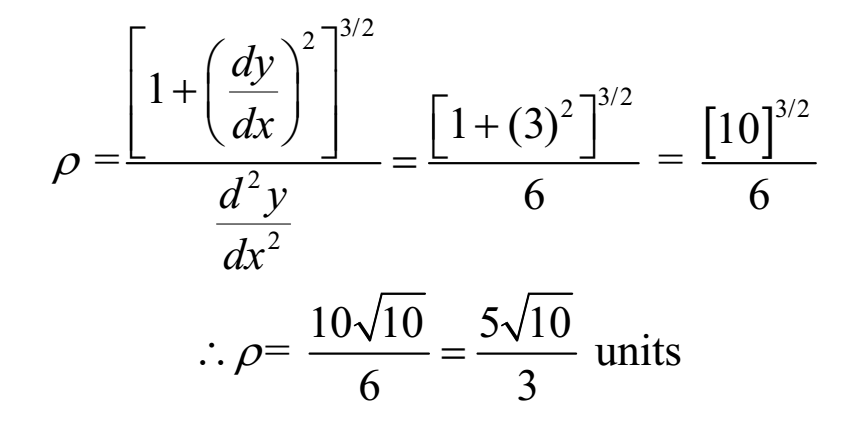
Ans: Radius of curvature of the given curve at (1, 1) is 5√10/3 units
Example 03:
Find the radius of curvature of the curve y = ex at (0, 1)
Solution:
Equation of curve is y = ex ………. (1)
Differentiating both sides w.r.t. x
(dy/dx) = ex ………………. (2)
(dy/dx) at P(1,1) = e1 = e
Differentiating equation (2) again w.r.t. x
(d2y/dx2) = ex ………………. (2)
(d2y/dx2) at P(1,1) = e1 = e

Ans: Radius of curvature of the given curve at (0, 1) is 2√2 units
Example 04:
Find the radius of curvature of the curve xy = c2 at (c, c)
Solution:
Equation of curve is xy = c2 ………. (1)
Differentiating both sides w.r.t. x
X(dy/dx) + y = 0
(dy/dx) = -y/x
(dy/dx) at P(c, c) = – c/c = – 1
Differentiating equation (2) again w.r.t. x


Ans: Radius of curvature of the given curve at (0, 1) is c√2 units
Example 05:
Find the radius of curvature of the curve y2 = 4x at (2, 2√2)
Solution:
Equation of curve is y2 = 4x ………. (1)
Differentiating both sides w.r.t. x
2y (dy/dx) = 4
(dy/dx) = 2/y ………………. (2)
(dy/dx) at P(2, 2√2) = 2/2√2 = 1/√2
Differentiating equation (2) again w.r.t. x
(dy2/dx2) = -2/y2 (dy/dx)
(dy2/dx2) = -2/y2 (2/y) = -4/y3 ………………. (3)
(d2y/dx2) at P(2, 2√2) = – 4/(2√2)3 = – 4/16√2 = – 1/4√2

Ans: Radius of curvature of the given curve at (2, 2√2) is – 6√ 3 units.
Example 06:
Find the radius of curvature at (3, – 4) to the curve x2 + y2 = 25
Solution:
Equation of curve is x2 + y2 = 25 ………. (1)
Differentiating both sides w.r.t. x
2x + 2y (dy/dx) = 0
2y (dy/dx) = – 2x
(dy/dx) = – x/y ………………. (2)
(dy/dx) at P(3, -4) = – (3/-4) = 3/4
Differentiating equation (2) again w.r.t. x


Radius of curvature of the given curve at (3, -4) is 5 units
Example – 07:
Find the radius of curvature of the curve √x + √y = 1 at (1/4, 1/4)
Solution:
Equation of curve is √x + √y = 1 ………. (1)
Differentiating both sides w.r.t. x

Differentiating equation (2) again w.r.t. x


Ans: Radius of curvature of the given curve is 1/√2 units.
Example 08:
Find the radius of curvature of the curve √x + √y = root a at (a/4, a/4)
Solution:
Equation of curve is √x + √y = 1 ………. (1)
Differentiating both sides w.r.t. x

Differentiating equation (2) again w.r.t. x


Ans: Radius of curvature of the given curve is a/√2 units.
Example 09:
Find the radius of curvature of the curve x2/3 + y2/3 = 2 at (1, 1)
Solution:
Equation of curve is x2/3 + y2/3 = 2 ………. (1)
Differentiating both sides w.r.t. x

Differentiating equation (2) again w.r.t. x


Ans: Radius of curvature of the given curve is 3√2 units.
Example 10:
Find the radius of curvature of the curve x4 + y4 = 2 at (1, 1)
Solution:
Equation of curve is x4 + y4 = 2 ………. (1)
Differentiating both sides w.r.t. x
4x3 + 4y3 (dy/dx) = 0
4y3 (dy/dx) = – 4x3
4y3 (dy/dx) = – x3/y3 ………………. (2)
(dy/dx) at P(1,1) = – 13/13= – 1
Differentiating equation (2) again w.r.t. x


Ans: Radius of curvature of the given curve at (1,1) is – √2/3 units