In this article, we shall study more examples to find the equation of normal and tangent to a curve at a given point.
Example – 12:
Find the equation of the tangent and normal to the curve x = sin θ and y = cos 2θ at θ = π/6
Solution:
The equation of the curve is x = sin θ and y = cos 2θ ………. (1)
Parameter θ = π/6
∴ x = sin π/6 = 1/2 and y = cos 2(π/6) = cos π/3 = ½
Therefore the point on the curve is P(1/2, 1/2)
Differentiating equation (1) w.r.t. x
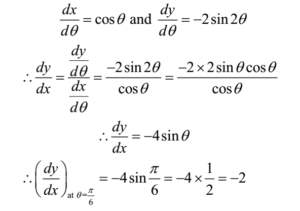
The slope of the tangent at P(1/2, 1/2) is -2 and that of normal is 1/2.
Equation of tangent:
Its slope = m = -2
It passes through P(1/2, 1/2) ≡ P(x1, y1)
By slope point form
y – y1 = m(x – x1)
∴ y – 1/2 = -2(x – 1/2)
∴ y – 1/2 = -2x + 1
∴ 2y – 1 = -4x + 2
∴ 4x + 2y – 3 = 0
Equation of normal:
By slope point form
y – y1 = m(x – x1)
∴ y – 1/2 = (1/2)(x – 1/2)
∴ 2y – 1 = x – 1/2
∴ 4y – 2 = 2x – 1
∴ 2x – 4y + 1= 0
Ans: Equation of tangent is 4x + 2y – 3 = 0 and that of normal is 2x – 4y + 1= 0
Example – 13:
Find the equation of the tangent and normal to the curve x = acos3θ and y = asin3θ at θ = π/4
Solution:
Equation of curve is x = acos3θ and y = asin3θ ………. (1)
Parameter θ = π/4
∴ x = acos3 (π/4) = a(1/√2)3 = a (1/2√2) = a/2√2
∴ y = asin3 (π/4) = a(1/√2)3 = a (1/2√2) = a/2√2
Therefore the point on the curve is P(a/2√2, a/2√2)
Differentiating equation (1) w.r.t. x
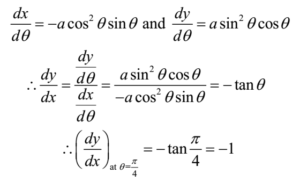
The slope of the tangent at P(a/2√2, a/2√2) is – 1 and that of normal is 1.
Equation of tangent:
Its slope = m = – 1
It passes through P(a/2√2, a/2√2) ≡ P(x1, y1)
By slope point form
y – y1 = m(x – x1)
∴ y – a/2√2 = -1(x – a/2√2)
∴ 2√2 y – a = – 2√2 x + a
∴ 2√2 x + 2√2 y – 2a = 0
∴ √2 x + √2 y –a = 0
Equation of normal:
By slope point form
y – y1 = m(x – x1)
∴ y – a/2√2 = 1(x – a/2√2)
∴ y – a/2√2 = x – a/2√2
∴ 2√2 y – a = 2√2 x – a
∴ 2√2 x – 2√2 y = 0
∴ x – y = 0
Ans: Equation of tangent is √2 x + √2 y – a = 0 and that of normal is x – y = 0
Example – 14:
Find the equation of the tangent and normal to the curve x = a sec θ and y = a tan θ at θ = π/6
Solution:
Equation of curve is x = a sec θ and y = a tan θ ………. (1)
Parameter θ = π/6
∴ x = a sec (π/6) = 2a/√3 and y = a tan (π/6) = a/√3
Therefore the point on the curve is P(2a/√3, a/√3)
Differentiating equation (1) w.r.t. x
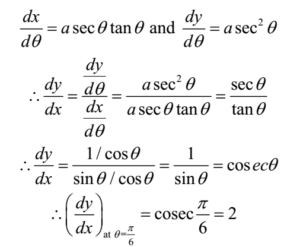
The slope of the tangent at P(2a/√3, a/√3) is 2 and that of normal is – 1/2.
Equation of tangent:
Its slope = m = 2
It passes through P(2a/√3, a/√3) ≡ P(x1, y1)
By slope point form
y – y1 = m(x – x1)
∴ y – a/√3 = 2(x – 2a/√3)
∴ y – a/√3 = 2x – 4a/√3
∴ √3 y – a = 2 √3 x – 4a
∴ 2√3 x – √3 y – 3a = 0
∴ 2x – y – √3a = 0
Equation of normal:
By slope point form
y – y1 = m(x – x1)
∴ y – a/√3 = (-1/2)(x – 2a/√3)
∴ 2y – 2a/√3= – x + 2a/√3
∴ 2√3 y – 2a = – √3 x + 2a
∴ √3 x + 2√3 y – 4a = 0
Ans: Equation of tangent is 2x – y – √3 a = 0 and that of normal is √3 x + 2√3 y – 4a = 0
Example – 15:
Find the equation of the tangent to the curve x = a(θ + sin θ) and y = a(1 + cos θ) at θ = π/2
Solution:
Equation of curve is x = a(θ + sin θ) and y = a(1 + cos θ) ………. (1)
Parameter θ = π/6
∴ x = a(θ + sin θ) = a(π/2 + sin π/2)=a(π/2 + 1) and
∴ y = a(1 + cos θ) = a(1 + cos π/2) = a(1 + 0) = a
Therefore the point on the curve is P(a(π/2 + 1), a)
Differentiating equation (1) w.r.t. x

The slope of the tangent at P(a(π/2 + 1), a) is -1 and that of normal is 1.
Equation of tangent:
Its slope = m = -1
It passes through P(a(π/2 + 1), a) ≡ P(x1, y1)
By slope point form
y – y1 = m(x – x1)
∴ y – a = -1(x – a(π/2 + 1))
∴ y – a = – x + a(π/2) + a
∴ x + y – a – a(π/2) – a = 0
∴ x – y – a(π/2) – 2a = 0
Ans: Equation of tangent is x – y – a(π/2) – 2a = 0
Example – 16:
Find the equation of tangent and normal to the curve x = 1/t and y = t – 1/t at t = 2
Solution:
Equation of curve is x = 1/t and y = t – 1/t ………. (1)
Parameter t = 2
∴ x = 1/2 and y = 2 – 1/2 = 3/2
Therefore the point on the curve is P(1/2, 3/2)
Differentiating equation (1) w.r.t. x

The slope of the tangent at P(1/2, 3/2) is -5 and that of normal is 1/5.
Equation of tangent:
Its slope = m = – 5
It passes through P(1/2, 3/2) ≡ P(x1, y1)
By slope point form
y – y1 = m(x – x1)
∴ y – 3/2 = – 5(x – 1/2)
∴ y – 3/2 = – 5x + 5/2
∴ 5x + y – 3/2 – 5/2 = 0
∴ 5x + y – 4 = 0
Equation of normal:
By slope point form
y – y1 = m(x – x1)
∴ y – 3/2 = 1/5(x – 1/2)
∴ 5y – 15/2 = x – 1/2
∴ x – 5y – 1/2 + 15/2 = 0
∴ x – 5y + 7 = 0
Ans: Equation of tangent is 5x + y – 4 = 0 and that of normal is x – 5y + 7 = 0
Example – 17:
Show that the tangent to the curve 8y = (x -2)2 at the point (-6, 8) is parallel to the tangent to the curve y = x + 3/x at point (1, 4)
Solution:
Consider the first curve 8y = (x -2)2
Differentiating both sides w.r.t. x
8 (dy/dx) = 2(x – 2) (1)
(dy/dx) = (x – 2)/4
∴ (dy/dx)at P(-6, 8) = (- 6 – 2)/4 = -8/4 = -2
Thus the slope of the tangent to curve 8y = (x -2)2
at the point (-6, 8) is – 2 ………….. (1)
Consider the second curve y = x + 3/x
Differentiating both sides w.r.t. x
(dy/dx) = 1 – 3/x2
∴ (dy/dx)at Q(1, 4) = 1- 3/12 = 1- 3 = -2
Thus slope of tangent to curve y = x + 3/x
at the point (1, 4) is – 2 ………….. (2)
From statements (1) and (2) we can see that the two slopes are equal.
Hence the two tangents are parallel to each other (proved as required)
Example – 18:
Show that the tangents to the curve x2 = 2y and 6y = 5 – 2x3 at x = 1 are perpendicular to each other.
Solution:
Consider the first curve x2 = 2y
Differentiating both sides w.r.t. x
2x = 2(dy/dx)
∴ (dy/dx) = x
∴ (dy/dx)at x = 1 = 1
Thus slope of tangent to curve x2 = 2y at x = 1 is 1 ………….. (1)
Consider the second curve 6y = 5 – 2x3
Differentiating both sides w.r.t. x
6dy/dx = -6x2
∴ (dy/dx) = -x2
∴ (dy/dx)at x = 1 = -(1)2 = -1
Thus slope of tangent to curve 6y = 5 – 2x3 at x = 1 is -1 ………….. (2)
From statements (1) and (2) we can see that the product of the two slopes is -1.
Hence the two tangents are perpendicular to each other (proved as required)
Example – 19:
Find the points on the curve y = 3x2 – 9x + 8 where the tangent is parallel to x- axis
Solution:
The tangent is parallel to x-axis hence its slope m = (dy/dx) = 0
The equation of the curve is y = 3x2 – 9x + 8 …………… (1)
Differentiating both sides w.r.t. x
(dy/dx) = 6x – 9
Thus 6x – 9 = 0
∴ 6x = 9
∴ x = 3/2
Substituting in equation (1)
y = 3(3/2)2 – 9(3/2) + 8= 3(9/4) – 27/2 + 8
∴ y = 27/4 -27/2 + 8 = -27/4 + 8 = 5/4
The point on the curve is (3/2, 5/4)
Example – 20:
Find the points on the curve y = 3x2 – 9x + 8 where the tangent makes an angle 45o with the x-axis
Solution:
The tangent makes an angle 45o with the x-axis
Slope of tangent = m = tan 45o = 1 = (dy/dx)
The equation of the curve is y = 3x2 – 9x + 8 …………… (1)
Differentiating both sides w.r.t. x
(dy/dx) = 6x – 9
Thus 6x – 9 = 1
∴ 6x = 10
∴ x = 5/3
Substituting in equation (1)
y = 3(5/3)2 – 9(5/3) + 8= 3(25/9) – 15 + 8
∴ y = 25/3 – 15 + 8 = 25/3 – 7 = 4/3
The point on the curve is (5/3, 4/3)
Example – 21:
Find the point on the curve y = √x – 3 where the tangent is perpendicular to the line 6x + 3y – 5 = 0
Solution:
Equation of given line 6x + 3y – 5 = 0
Slope of given line = – (coefficient of x/coefficient of y) = – (6/3) = – 2
As the tangent is perpendicular to given line
Slope of tangent = 1/2
Equation of curve is y = √x – 3
Differentiating both sides w.r.t. x

squaring both sides
1 = x – 3
∴ x = 4
Substituting in equation (1)
y = √4 – 3 = √1 = ±1
The points on the curve are (4, 1) and (4, -1)
Example – 22:
Find the coordinates of the point on the curve y = x – 4/x, where the tangent at that point is parallel to the line y = 2x.
Solution:
Equation of given line y = 2x
Slope of given line = 2
Now the tangent is parallel to the given line
Slope of tangent = m = 2 = (dy/dx)
Equation of the curve is y = x – 4/x
Differentiating both sides w.r.t.x
(dy/dx) = 1 – 4(- 1/x2) = 1 + 4/x2
∴ 1 + 4/x2 = 2
∴ 4/x2 = 1
∴ x2 = 4
∴ x = ± 2
When x = 2
y = 2 – 4/2 = 2 – 2 = 0
Hence the point is (2, 0)
When x = -2
y = – 2 – 4/(-2) = – 2 + 2 = 0
Hence the point is (- 2, 0)
The required points are (2, 0) and (-2, 0)
Example – 23:
If the line x + y = 0 touches the curve 2y2 = ax2 + b at (1, -1) find a and b
Solution:
Equation of tangent is x + y = 0
Slope of tangent = – (coefficient of x/coefficient of y) = – (1/1) = -1
Equation of curve is 2y2 = ax2 + b
Differentiating both sides w.r.t. x
4y (dy/dx) = 2ax
∴ (dy/dx)=ax/2y
∴ (dy/dx)at P(1, -1) = a(1)/2(-1) = – a/2
– a/2 = -1
∴ a = 2
Point (1, -1) lies on the curve 2y2 = ax2 + b
2(-1)2 = 2(1)2 + b
∴ 2 = 2 + b
∴ b = 0
Ans: a = 2 and b = 0
Example – 24:
For the curve y = 3x – 2x2, find the equation of the tangent whose slope is – 1.
Solution:
Slope of tangent = -1
Equation of curve is y = 3x – 2x2 ………. (1)
Differentiating both sides w.r.t. x
(dy/dx) = 3 – 4x
∴ 3 – 4x = -1
∴ 4 = 4x
∴ x = 1
Substituting in equation (1)
y = 3(1) – 2(1)2 = 3 – 2 = 1
The tangent touches the curve at (1, 1) ≡ P(x1, y1) and its slope = m = -1
By slope point form
y – y1 = m(x – x1)
∴ y – 1 = – 1(x – 1)
∴ y – 1 = – x + 1
∴ x + y – 2 = 0
Ans: The equation of tangent is x + y – 2 = 0
Example – 25:
Find equations of tangents and normal to the curve y = 6 – x2, where the normal is parallel to the cline x – 4y + 3 = 0
Solution:
Equation of given line x – 4y + 3 = 0
Slope of given line = – (coefficient of x/coefficient of y) = – (1/-4) = 1/4
As the normal is perpendicular to given line
Slope of normal = 1/4
Slope of tangent = – 4
The equation of curve isy = 6 – x2
Differentiating both sides w.r.t. x
(dy/dx) = – 2x = – 4
x = 2
Substituting in equation of curve
y = 6 – 22 = 6 – 4 = 2
The tangent touches the curve at (2, 2)
Equation of tangent:
Its slope = m = – 4
It passes through P(2, 2) ≡ P(x1, y1)
By slope point form
y – y1 = m(x – x1)
∴ y – 2 = – 4(x – 2)
∴ y – 2 = – 4x + 8
∴ 4x + y – 10 = 0
Equation of normal:
Its slope = m = 1/4
It passes through P(2, 2) ≡ P(x1, y1)
By slope point form
y – y1 = m(x – x1)
∴ y – 2 = 1/4(x – 2)
∴ 4y – 8 = x – 2
∴ x – 4y + 6 = 0
Ans: Equation of tangent is 4x + y – 10 = 0 and that of normal is x – 4y + 6 = 0
Example – 26:
If the line y = 4x -5 touches the curve y2 = ax3 + b at the point (2, 3) show that 7a + 2b = 0
Solution:
Equation of tangent is 4x – y -5 = 0
Slope of the tangent = – (coefficient of x/coefficient of y) = – (4/-1) = 4 = (dy/dx)
Equation of curve is
y2 = ax3 + b
Differentiating both sides w.r.t. x
2y(dy/dx) = 3ax2
∴ (dy/dx) = 3ax2/2y
∴ (dy/dx) at(2, 3) = 3a(2)2/ 2(3)= 2a
Thus slope of tangent to the curve at (2, 3) is 2a
2a = 4
∴ a = 2
Now point (2, 3) lies on the curve y2 = ax3 + b
32 = 2(2)3 + b
∴ 9 = 16 + b
∴ b = 9 – 16 = -7
To prove that 7a + 2b = 0
L.H.S. = 7a + 2b = 7(2) + 2(-7) = 14 – 14 = 0 = R.H.S.
∴ 7a + 2b = 0 (Proved as required)