Equations of Tangents and Normals

In this article, we shall study the use of the concept of differentiation to find slope, equation of tangent, and normal.

Example – 01:

Find the equation of the tangent and normal to the curve y = 3x² – x + 1 at point P(1, 3)

Solution:

Equation of curve is y = 3x² – x + 1    ………… (1)

Differentiating equation (1) w.r.t. x

(dy/dx) = 6x – 1

∴  (dy/dx)_{at P(1, 3)} = 6(1) – 1 = 6 – 1 = 5

The slope of the tangent at P(1, 3) is 5 and that of normal is – 1/5.

Equation of tangent:

Its slope = m = 5

It passes through P(1, 3) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 3 = 5(x – 1)

∴  y – 3 = 5x – 5

∴  5x – y – 2 = 0

Equation of normal:

Its slope = m = – 1/5

It passes through P(1, 3) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 3 = (- 1/5)(x – 1)

∴  5y – 15 = -x + 1

∴  x + 5y -15 – 1 = 0

∴  x + 5y – 16 = 0

Ans: Equation of tangent is 5x – y – 2 = 0 and that of normal is x + 5y – 16 = 0

Example – 02:

Find the equation of the tangent and normal to the curve y = x² + 4x + 1 = 0 at point P(-1, -2)

Solution:

Equation of curve is y = x² + 4x + 1    ………… (1)

Differentiating equation (1) w.r.t. x

(dy/dx) = 2x + 4

∴  (dy/dx)_{at P(-1, -2)} = 2(-1) + 4 = -2 + 4 = 2

The slope of the tangent at P(-1, -2) is 2 and that of normal is – 1/2.

Equation of tangent:

Its slope = m = 2

It passes through P(-1, -2) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y + 2 = 2(x + 1)

∴  y + 2 = 2x + 2

∴  2x – y = 0

Equation of normal:

Its slope = m = -1/2

It passes through P(-1, -2) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y + 2 = (- 1/2)(x + 1)

∴  2y + 4  = -x – 1

∴  x + 2y + 5= 0

Ans: Equation of tangent is 2x – y = 0 and that of normal is x + 2y + 5= 0

Example – 03:

Find the equation of the tangent and normal to the curve 2x² + 3y² – 5 = 0 at point P(1, 1)

Solution:

Equation of curve is 2x² + 3y² – 5 = 0     ………… (1)

Differentiating equation (1) w.r.t. x

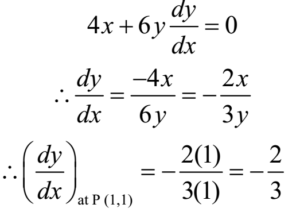
The slope of the tangent at P(1, 1) is – 2/3 and that of normal is 3/2.

Equation of tangent:

Its slope = m = – 2/3

It passes through P(1, 1) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 1 =(- 2/3)(x – 1)

∴  3y – 3 = -2x + 2

∴  2x + 3y – 5 = 0

Equation of normal:

Its slope = m = 3/2

It passes through P(1, 1) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 1 =(3/2)(x – 1)

∴  2y – 2 = 3x – 3

∴  3x – 2y – 1 = 0

Ans: Equation of tangent is 2x + 3y – 5 = 0 and that of normal is 3x – 2y – 1 = 0

Example – 04:

Find the equation of the tangent and normal to the curve x² + y³ + xy = 3 at point P(1, 1)

Solution:

Equation of curve is x² + y³ + xy = 3      ………… (1)

Differentiating equation (1) w.r.t. x

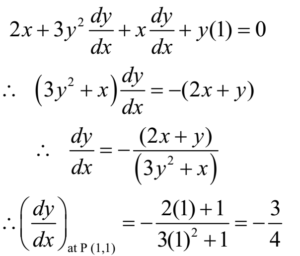
The slope of the tangent at P(1, 1) is – 3/4 and that of normal is 4/3.

Equation of tangent:

Its slope = m = – 4/3

It passes through P(1, 1) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 1 =(- 3/4)(x – 1)

∴  4y – 4 = -3x + 3

∴  3x + 4y – 7 = 0

Equation of normal:

Its slope = m = 3/4

It passes through P(1, 1) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 1 =(4/3)(x – 1)

∴  3y – 3 = 4x – 4

∴  4x – 3y – 1 = 0

Ans: Equation of tangent is 3x + 4y – 7 = 0 and that of normal is 4x – 3y – 1 = 0

Example – 05:

Find the equation of the tangent and normal to the curve xy = c² at point P(ct, c/t). Where t is a parameter

Solution:

Equation of curve is xy = c²     ………… (1)

Differentiating equation (1) w.r.t. x

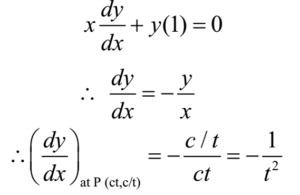
The slope of the tangent at P(ct, c/t) is – 1/t² and that of normal is t².

Equation of tangent:

Its slope = m = – 1/t²

It passes through P(ct, c/t) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – c/t =(- 1/t²)(x – ct)

∴  t² (y – c/t) = – x + ct

∴  y t² – ct = – x + ct

∴  x + y t² – 2ct = 0

Equation of normal:

Its slope = m = t²

It passes through P(ct, c/t) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – c/t = t²(x – ct)

∴  yt – c  = t³(x – ct)

∴  yt – c  = x t³ – c t⁴

∴  t³x – yt + c – c t⁴ = 0

Ans: Equation of tangent is x + y t² – 2ct = 0 and that of normal is t³x – yt + c – c t⁴ = 0

Example – 06:

Find the equation of the tangent and normal to the curve √x – √y = 1 at P(9, 4)

Solution:

Equation of curve is √x – √y = 1     ………… (1)

Differentiating equation (1) w.r.t. x

The slope of the tangent at P(9, 4) is 2/3 and that of normal is -3/2.

Equation of tangent:

Its slope = m = 2/3

It passes through P(9, 4) ≡ P(x₁, y₁)\

By slope point form

y – y₁ = m(x – x₁)

∴  y – 4 =(2/3)(x – 9)

∴  3y – 12 = 2x – 18

∴  2x – 3y – 6 = 0

Equation of normal:

By slope point form

y – y₁ = m(x – x₁)

∴  y – 4 =(- 3/2)(x – 9)

∴  2y – 8 = – 3x + 27

∴  3x + 2y – 35 = 0

Ans: Equation of tangent is 2x – 3y – 6 = 0 and that of normal is 3x + 2y – 35 = 0

Example – 07:

Find the equation of the tangent and normal to the curve y = x³ – x² – 1 at a point whose abscissa is -2.

Solution:

Equation of curve is y = x³ – x² – 1   ………… (1)

Let P be the point whose abscissa (x-coordinate) is -2

Substituting in equation (1)

y = x³ – x² – 1 = (-2)³ – (-2)² – 1 = – 8 – 4 – 1 = -13

Hence coordinates of point P are (-2, -13)

Differentiating equation (1) w.r.t. x

(dy/dx) = 3x² – 2x

∴  (dy/dx)_{at P(-2, -13)} = 3(-2)² – 2(-2) = 12 + 4 = 16

The slope of the tangent at P(-2, -13) is 16 and that of normal is – 1/16.

Equation of tangent:

Its slope = m = 16

It passes through P(-2, -13) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y + 13 = 16 (x + 2)

∴  y + 13 = 16x + 32

∴  16x – y +32 -13 = 0

∴  16x – y + 19 = 0

Equation of normal:

Its slope = m = 1- 1/6

It passes through P(-2, -13) ≡ P(x₁, y₁)

slope point form

y – y₁ = m(x – x₁)

∴  y + 13 = (-1/16) (x + 2)

∴  16y + 208 = – x – 2

∴  x + 16y + 208 + 2 = 0

∴  x + 16y + 210 = 0

Ans: Equation of tangent is 16x – y + 19 = 0 and that of normal is x + 16y + 210 = 0

Example – 08:

Find the equation of the tangent and normal to the curve y = x² + 4x at a point whose ordinate is -3.

Solution:

Equation of curve is y = x² + 4x         ………… (1)

Let P be the point whose ordinate (y-coordinate) is -3

Substituting in equation (1)

y = x² + 4x = – 3

∴  x² + 4x + 3 = 0

∴  (x + 3)(x + 1) = 0

∴  x + 3 = 0 or/and x + 1 = 0

∴  x = -3 or/and x = -1

Hence the points are P(-3, -3) and Q (-1, -3)

Differentiating equation (1) w.r.t. x

(dy/dx) = 2x + 4

Let us consider point P(-3, -3)

(dy/dx)_{at P(-3, -3)} = 2(-3) + 4 = – 6 + 4 = – 2

The slopes of the f tangent at P(-3, -3) is -2 and that of normal is 1/2.

• Equation of tangent:

Its slope = m = -2

It passes through P(-3, -3) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y + 3 = -2 (x + 3)

∴  y + 3 = – 2x – 6

∴  2x + y + 9 = 0

• Equation of normal:

Its slope = m = 1/2 It passes through P(-3, -3) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y + 3 = (1/2)(x + 3)

∴  2y + 6 = x + 3

∴  x – 2y – 3= 0

Let us consider point P(-1, -3)

(dy/dx)_{at P(-1, -3)} = 2(-2) + 4

The slope of the tangent at P(-1, -3) is 2 and that of normal is – 1/2.

• Equation of tangent:

Its slope = m = 2

It passes through P(-1, -3) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y + 3 = 2 (x + 1)

∴  y + 3 =  2x + 2

∴  2x – y – 1 = 0

• Equation of normal:

Its slope = m = – 1/2

It passes through P(-1, -3) ≡ P(x₁, y₁)

By slope point form

∴  y – y₁ = m(x – x₁)

∴  y + 3 = (-1/2)(x + 1)

∴  2y + 6 = – x – 1

∴  x + 2y + 7 = 0

Ans: At point (-3, -3) equation of tangent is 2x + y + 9 = 0 and that of normal is x – 2y – 3= 0

At point (-1, -3) equation of tangent is 2x – y – 1 = 0 and that of normal is x + 2y + 7 = 0

Example – 09:

Find the equation of the tangent and normal to the curve y = x² – 5x at a point where the curve meets the x-axis.

Solution:

The equation of the curve is y = x² – 5x  …………….. (1)

Let P be the point at which the curve meets x-axis (y = 0).

Substituting y = 0 in equation (1)

0 = x² – 5x

∴  x(x – 5) = 0

∴  x = 0 or x = 5

Hence the curve cuts x-axis at P(0, 0) and Q(5, 0)

Differentiating equation (1) w.r.t. x

(dy/dx) = 2x – 5

Consider point P(0, 0)

(dy/dx)_{at P(0, 0)} = 2(0) – 5 = -5

The slope of the tangent at P(0, 0) is – 5 and that of normal is 1/5.

• Equation of tangent:

Its slope = m = – 5

It passes through P(0, 0) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 0 = -5 (x – 0)

∴  y = – 5x

∴  5x + y = 0

• Equation of normal:

Its slope = m = 1/5

It passes through P(0, 0) ≡ P(x₁, y₁)

By slope point form

∴  y – y₁ = m(x – x₁)

∴  y – 0 = (1/5) (x – 0)

∴  5y = x

∴  x – 5y = 0

Consider point P(5, 0)

(dy/dx)_{at P(0, 0)} = 2(5) – 5 = 5

The slope of the tangent at P(0, 0) is 5 and that of normal is – 1/5.

• Equation of tangent:

Its slope = m =  5

It passes through P(5, 0) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 0 = 5 (x – 5)

∴  y =  5x – 25

∴  5x – y – 25 = 0

• Equation of normal:

Its slope = m =  – 1/5

It passes through P(5, 0) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 0 = (-1/5) (x – 5)

∴  5y = – x + 5

∴  x + 5y – 5 = 0

Ans: At point (0, 0) equation of tangent is 5x + y = 0 and that of normal is x – 5y = 0

At point (5, 0) equation of tangent is 5x – y – 25 = 0 and that of normal is x + 5y – 5 = 0

Example – 10:

Find the equation of the tangent and normal to the curve y = x² + 4x at the point where it cuts the y-axis

Solution:

Equation of curve is y = x² + 4x    ………… (1)

Let P be the point at which the curve cuts y-axis (x = 0).

Substituting x = 0 in equation (1)

y = 0² – 5(0) = 0

Hence the curve cuts x-axis at P(0, 0)

Differentiating equation (1) w.r.t. x

(dy/dx) = 2x + 4

(dy/dx)_{at P(0, 0)} = 2(0) + 4 = 0 + 4 = 4

The slope of the tangent at P(0, 0) is 4 and that of normal is – 1/4.

Equation of tangent:

Its Slope = m = 4

It passes through P(0, 0) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 0 = 4(x – 0)

∴  y = 4x

∴  4x – y = 0

Equation of normal:

Its Slope = m = -1/4

It passes through P(0, 0) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 0 = (-1/4) (x – 0)

∴  4y = – x

∴  x + 4y = 0

Example – 11:

Find the equation of the tangent and normal to the curve y = √2 sin (2x + π/4) at x = π/4

Solution:

Equation of curve is y = √2 sin (2x + π/4)         ………… (1)

Substituting x = π/4 in equation (1)

y = √2 sin (2(π/4) + π/4) = √2 sin (π/2 + π/4) =√2 cos π/4 = √2 x (1/√2 )= 1

Therefore the coordinates of point P are (π/4, 1)

Differentiating equation (1) w.r.t. x

(dy/dx) = √2 cos (2x + π/4). 2

∴  (dy/dx) = 2√2 cos (2x + π/4)

∴  (dy/dx)_{at P(π/4, 1)} = 2√2 cos (2(π/4) + π/4)

∴  (dy/dx)_{at P(π/4, 1)} = 2√2 cos (π/2 + π/4)

∴  (dy/dx)_{at P(π/4, 1)} = – 2√2 sin (π/4)

∴  (dy/dx)_{at P(π/4, 1)} = – 2√2 x (1/√2 ) = – 2

The slope of the tangent at P(9, 4) is -2 and that of normal is 1/2.

Equation of tangent:

Its slope = m = -2

It passes through P(π/4, 1) ≡ P(x₁, y₁)

By slope point form

y – y₁ = m(x – x₁)

∴  y – 1 = -2(x – π/4)

∴  y – 1 = -2x + π/2

∴  2x + Y – 1 – π/2 = 0

Equation of normal:

Its slope = m = 1/2

It passes through P(π/4, 1) ≡ P(x₁, y₁)

By slope point form

 y  – y₁ = m(x – x₁)

∴  y – 1 = (1/2)(x – π/4)

∴  2y – 2 = x – π/4

∴  x – 2y + 2 – π/4 = 0

Ans: Equation of tangent is 2x + Y – 1 – π/2 = 0 and that of normal is x – 2y + 2 – π/4 = 0