In this article, we shall find the maximum and minimum value of the given function.
Example – 01:
If x + y = 3 show that the maximum value of x2 y is 4
Solution:
Given x + y = 3
hence y = 3 – x
∴ x2 y = x2(3 – x) = 3x2 – x3
Let ƒ(x) = 3x2 – x3 ………….. (1)
Differentiating equation (1) w.r.t. x
ƒ’(x) = 6x – 3x2 ………….. (2)
Differentiating equation (2) w.r.t. x
ƒ’’(x) = 6 – 6x ………….. (3)
For maximum or minimum value ƒ’(x) = 0
6x – 3x2 = 0
∴ 3x(2 – x) = 0
∴ x = 0 or/and 2- x = 0
∴ x = 0 or/and x = 2
Let us consider x = 0
ƒ’’(0) =6 – 6(0) = 6 – 0 = 6 > 0
Hence the function is increasing at x = 0 and has minimum value at x = 0
Let us consider x = 3
ƒ’’(2) = 6 – 6(2) = 6 – 12 = -6 < 0
Hence the function is decreasing at x = 2 and has maximum value at x = 2
Substituting x = 2 in equation (1)
Maximum value = ƒ(2) = 3(2)2 – (2)3 = 12 – 8 = 4
Thus the maximum value is 4 (Proved as required)
Example – 02:
show that f(x) = xx is minimum when x = 1/e
Solution:
Let ƒ(x) = xx ………….. (1)
Differentiating equation (1) w.r.t. x
ƒ’(x) = xx(1 + logx)
Differentiating equation (2) w.r.t. x
ƒ’'(x) = xx(0 + 1/x) + (1 + logx)xx(1 + logx)
ƒ’'(x) = xx/x + xx(1 + logx)2
ƒ’'(x) = (1/x + 1(1 + logx)2) ………….. (3)
For maximum or minimum value ƒ’(x) = 0
xx(1 + logx) = 0
∴ xx = 0 or/and (1 + logx) = 0
xx = 0 implies x = 0 makes term logx resundant
Hence x = 0 is not possible
∴ (1 + logx) = 0
∴ log x = -1
∴ x = e-1
∴ x = 1/e
ƒ’’(1/e) = (1/(1/e) + 1(1 + log(1/e))2)
ƒ’’(1/e) = (e + 1(1 – loge)2) = (e + 0) = e > 0
Hence the function is increasing at x = 1/e and has minimum value at x = 1/e (Proved as required)
Example – 03:
show that f(x) = (logx)/x (x ≠ 0) is maximum at x = e
Solution:

For maximum or minimum value ƒ’(x) = 0
(1 – logx)/x2 = 0
∴ (1 – logx) = 0
∴ log x = 1
∴ x = e1
∴ x = e
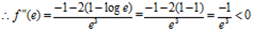
Hence the function is decreasing at x = e and has maximum value at x = e (Proved as required)
Example – 04:
Find the maximum and minimum values of x2.ex.
Solution:
Let ƒ(x) = x2.ex ………….. (1)
Differentiating equation (1) w.r.t. x
ƒ’(x) = x2.ex + ex. 2x
ƒ’(x) = x2.ex + 2 x ex………….. (2)
Differentiating equation (2) w.r.t. x
ƒ’’(x) = x2.ex + ex. 2x + 2(x ex + ex(1))
ƒ’’(x) = x2.ex + 2x ex + 2x ex + 2ex
ƒ’’(x) = ex(x2 + 2x + 2x + 2)
ƒ’’(x) = ex(x2 + 4x + 2)………….. (3)
For maximum or minimum value ƒ’(x) = 0
x2.ex + 2 x ex = 0
∴ x.ex ( x + 2) = 0
ex ≠ 0
∴ x = 0 or/and x + 2 = 0
∴ x = 0 or/and x = – 2
Let us consider x = 0
ƒ’’(0) = e0(02 + 4(0) + 2) = 1(0 + 0 + 2) = 2 > 0
Hence the function is increasing at x =0 and has minimum value at x = 0
Substituting x = 0 in equation (1)
Minimum value = ƒ(2) = 02.e0 = 0
Thus point of minimum is (0, 0)
Let us consider x = – 2
ƒ’’(-2) = e-2((-2)2 + 4(-2) + 2) = e-2(4 – 8 + 2) = – 2/e2 < 0
Hence the function is decreasing at x = – 2 and has maximum value at x = -2
Substituting x = – 2 in equation (1)
Maximum value = ƒ(-2) = (-2)2.e-2 = 4/e2
Thus point of maximum is (- 2, 4/e2)
Ans: The maximum value is 4/e2 at x = -2 and
minimum value is -0 at x = 0
Example – 05:
Find extreme values of ƒ(x) = a sin x + b cos x
Solution:
Let ƒ(x) = ƒ(x) = a sin x + b cos x ………….. (1)
Differentiating equation (1) w.r.t. x
ƒ’(x) = ƒ(x) = a cosx – b sin x ………….. (2)
Differentiating equation (2) w.r.t. x
ƒ’’(x) = – a sin x – b cos x = – ƒ(x) ………….. (3)
For maximum or minimum value ƒ’(x) = 0
a cosx – b sin x = 0
a cosx = b sin x
Squaring both sides
a2 cos2x = b2 sin2 x
a2 (1 – sin2x) = b2 sin2 x
a2 – a2sin2x)= b2 sin2 x
a2 = a2sin2x + b2 sin2 x
a2 = (a2 + b2)sin2 x
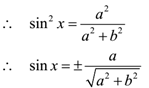



Hence the function is increasing and has a minimum value

Hence the function is increasing and has a minimum value
