Science > Mathematics > Pair of Straight Lines > Combined Equation of Lines When Inclinations are Given
In this article, we shall study to find a combined equation of pair of lines when the inclinations of lines are given.
Algorithm:
- If θ is the inclination of a line, then its slope is given by m = tan θ.
- Find slopes m1 and m2 of the two lines.
- Use y = mx form to find equations of the two lines.
- Write equations of lines in the form u = 0 and v = 0.
- Find u.v = 0.
- Simplify the L.H.S. of the joint equation.
Example 01:
- Find the combined equation of the lines passing through the origin and making an angle of 30° with the positive direction of the x-axis
- Solution:
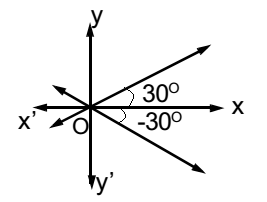
Slope of the first line = m1 = tan 30° = 1/√3
The equation the first line is y = m1 x
y = 1/√3 x
√3 y = x
x – √3 y = 0 …………. (1)
Slope of the second line = m2 = tan (-30°)= – tan 30° = -1/√3
The equation the second line is y = m2 x
y =- 1/√3x
√3 y = – x
x + √3 y = 0 …………. (2)
Their joint equation is (x – √3 y) (x + √3 y) = 0
x² – 3y² = 0
This is the required combined equation.
Example 02 :
- Find the combined equation of the lines passing through the origin and making an angle of 45° with the positive direction of the x-axis
- Solution:
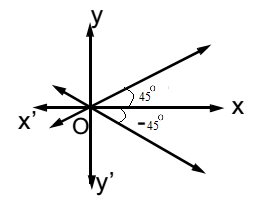
Slope of the first line = m1 = tan 45° = 1
The equation the first line is y = m1 x
y = 1.x
x – y = 0 …………. (1)
Slope of the second line = m2 = tan (-45°)= – tan 45° = -1
The equation the second line is y = m2 x
y = – 1 x
x + y = 0 …………. (2)
Their joint equation is (x – y) (x + y) = 0
x² – y² = 0
This is the required combined equation.
Example 03:
- Find the combined equation of the lines passing through the origin and making an angle of 60° with the positive direction of the x-axis.
- Solution:

Slope of the first line = m1 = tan 60° = √3
The equation the first line is y = m1 x
y = √3x
√3 x – y = 0 …………. (1)
Slope of the second line = m2 = tan (-60°)= – tan 60° = -√3
The equation the second line is y = m2 x
y =- √3x
√3 x + y = 0 …………. (2)
Their joint equation is (√3 x – y) (√3 x + y) = 0
3x² – y² = 0
This is the required combined equation.
Example 04:
- Find the combined equation of the lines passing through the origin and making an angle of 60° with the y-axis
- Solution:

Slope of the first line = m1 = tan 30° = 1/√3
The equation the first line is y = m1 x
y = 1/√3x
√3 y = x
x – √3 y = 0 …………. (1)
Slope of the second line = m2 = tan (150°)= tan(180° – 30°) = -tan 30° = -1/√3
The equation the second line is y = m2 x
y =- 1/√3x
√3 y = – x
x + √3 y = 0 …………. (2)
Their joint equation is (x – √3 y) (x + √3 y) = 0
x² – 3y² = 0
This is the required combined equation.
Example 05:
- Find the joint equation of a pair of lines through the origin having and having inclination 30° and 150°.
- Solution:
Slope of the first line = m1 = tan 30° = 1/√3
The equation the first line is y = m1 x
y = 1/√3x
√3 y = x
x – √3 y = 0 …………. (1)
Slope of the second line = m2 = tan (150°)= tan(180° – 30°) = -tan 30° = -1/√3
The equation the second line is y = m2 x
y =- 1/√3x
√3 y = – x
x + √3 y = 0 …………. (2)
Their joint equation is (x – √3 y) (x + √3 y) = 0
x² – 3y² = 0
This is the required combined equation.
Example 06:
- Find the joint equation of a pair of lines through the origin having and having inclination 60° and 120°
- Solution:
Slope of the first line = m1 = tan 60° = √3
The equation the first line is y = m1 x
y = √3x
√3 x – y = 0 …………. (1)
Slope of the second line = m2 = tan (120°)= tan (180° – 60°) = – tan 60° = -√3
The equation the second line is y = m2 x
y =- √3x
√3 x + y = 0 …………. (2)
Their joint equation is (√3 x – y) (√3 x + y) = 0
3x² – y² = 0
This is the required combined equation.
Example 07:
Find the joint equation of a pair of lines through the origin having and having inclination π/3 and 5π/3.
Solution:
Slope of the first line = m1 = tan π/3 = √3
The equation the first line is y = m1 x
y = √3x
√3 x – y = 0 …………. (1)
Slope of the second line = m2 = tan (5π/3)= tan (2π – π/3) = – tan π/3 = -√3
The equation the second line is y = m2 x
y =- √3x
√3 x + y = 0 …………. (2)
Their joint equation is (√3 x – y) (√3 x + y) = 0
3x² – y² = 0
This is the required combined equation.
Example 08:
- Find the joint equation of the straight lines through the origin which forms the equilateral triangle with the straight line x = 1.
- Solution:

Let OA and OB be two lines such that triangle OAB is an equilateral triangle.
Equation of AB is x = 1 and AB, is parallel to the y-axis.
Now triangle OAB is an equilateral triangle,
by symmetry, m ∠ MOA = m ∠MOB = 30°
Slope of OA = m1 = tan(-30°) = – tan 30° = – 1/√3 and
Slope of OB = m2 = tan( 30°) = 1/√3
Equation of OA is passing through the origin, is
y = m1x. i.e. y = – 1/√3 x
∴ √3 y = – x
∴ x + √3 y = 0 …….. (1)
As OB is also passing through the origin, the form of the equation of OB is
y = m2x. i.e. y = 1/√3 x
∴ √3 y = x
∴ x – √3 y = 0 …….. (2)
Hence, the combined equation of the pair OA and OB is
(x + √3 y)(x – √3 y ) = 0
∴ x 2 – 3y 2 = 0.
This is the required combined equation.
Note: The joint equation of the straight lines through the origin which forms the equilateral triangle with any straight line x = k is always x 2 – 3y 2 = 0.
Example 09:
- Find the joint equation of the straight lines through the origin which forms the equilateral triangle with the straight line y = 2.
- Solution:

Let OA and OB be two lines such that the triangle OAB is an equilateral triangle.
The equation of AB is y = 2 and AB is parallel to the x-axis.
Now since triangle OAB is an equilateral triangle,
m ∠ XOA = 60° and m ∠ XOB = 120°
∴ Slope of OA = tan 60° = √3 and
∴ slope of OB = tan 120° = – √3
As OA is passing through the origin, the form of equation of OA is
y = m1x. i.e. y = √3 x
∴ √3 x – y = 0 ………. (1)
As OB is also passing through the origin, the form of equation of OB is y = mx.
y = m2x. i.e. y = – √3 x
∴ √3 x + y = 0 ………. (2)
Hence their combined equation is
( √3 x – y)( √3 x + y) = 0
∴ 3x2 – y2 = 0.
This is the required combined equation.
Note: The joint equation of the straight lines through the origin which forms the equilateral triangle with any straight line y = k is always 3x2 – y2 = 0.