Science > Mathematics > Pair of Straight Lines > Combined Equation of Lines when Separate Equations are Given
In this article, we shall study to find a combined equation of pair of lines when a separate equation of each line is given.
Algorithm:
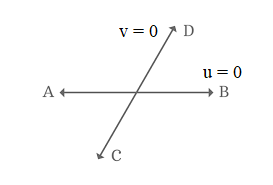
- Write equations of lines in the form u = 0 and v = 0.
- Find u.v = 0.
- Simplify the L.H.S. of the joint equation.
Example 01:
- Obtain the joint equation of the co-ordinate axes.
- Solution:
Equation of the x-axis is y = 0 .
Equation of the y-axis is x = 0
The joint equation of the two co-ordinate axis is x y = 0
Example 02:
- Find the joint equation of the two lines whose separate equations are 3x – 2y = 0 and 4x + y = 0.
- Solution:
Equation of the first line is 3x -2y = 0
Equation of the second line is 4x + y= 0
Thus the joint equation of a line is given by
(3x – 2y)(4x + y) = 0
∴ 3x (4x + y) – 2y (4x + y) = 0
∴ 12x² + 3xy – 8xy – 2y² = 0
∴ 12x² – 5xy – 2y² = 0
This is the required combined equation.
Example 03:
- Find the combined equation of the two lines whose separate equations are 3x + 4y = 0 and 2x = 3y
- Solution:
Equation of the first line is 3x + 4y = 0
Equation of the second line is 2x = 3y i.e 2x – 3y = 0
Thus the joint equation of a line is given by
(3x + 4y)(2x – 3y ) = 0
∴ 3x (2x – 3y) + 4y (2x – 3y ) = 0
∴ 6x² – 9xy + 8xy – 12y² = 0
∴ 6x² – xy – 12y² = 0
This is the required combined equation.
Example 04:
- Find the combined equation of the lines whose separate equations are 2x + y = 0 and 3x – 5y = 0.
- Solution:
Given equations of lines are 2x + y = 0 and 3x – 5y = 0
(2x + y )(3x – 5y) = 0
∴ 2x(3x – 5y) + y(3x – 5y) = 0
∴ 6x² – 10xy + 3xy – 5y² = 0
∴ 6x² – 7xy – 5y² = 0
This is the required combined equation.
Example 05:
- Find the combined equation of the lines whose separate equations are 3x – 2y + 1 = 0 and 4x – 3y + 5 = 0
- Solution:
Given equations of lines are 3x – 2y + 1 = 0 and 4x – 3y + 5 = 0
(3x – 2y + 1)(4x – 3y + 5) = 0
3x(4x – 3y + 5) – 2y(4x – 3y + 5) + 1(4x – 3y + 5) =
∴ 12x² – 9xy + 15x – 8xy + 6y² – 10y + 4x – 3y + 5 = 0
∴ 12x² – 17 xy + 6y² + 19x – 13y + 5 = 0
This is the required combined equation.
Example 06:
- Find the combined equation of the lines whose separate equations are x + y = 3 and 2x + y – 1 = 0.
- Solution:
Given equations of lines are x + y – 3 = 0 and 2x + y – 1 = 0
(x + y – 3)(2x + y – 1) = 0
x(2x + y – 1) + y(2x + y – 1) – 3(2x + y – 1) = 0
∴ 2x² + xy – x + 2xy + y² – y – 6x – 3y + 3 = 0
∴ 2x² + 3xy + y² – 7x – 4y + 3 = 0
This is the required combined equation.
Example 07:
- Find the combined equation of the lines whose separate equations are 3x + 2y – 1 = 0 and x + 3y – 2 = 0.
- Solution:
Given equations of lines are 3x + 2y -1 = 0 and x + 3y -2 = 0.
(3x + 2y -1 )(x + 3y -2) = 0
3x(x + 3y -2) + 2y(x + 3y -2) – 1(x + 3y -2) = 0
∴ 3x² + 9xy – 6x + 2xy + 6y² – 4y – x – 3y + 2 = 0
∴ 3x² + 11xy + 6y² – 7x – 7y + 2 = 0
This is the required combined equation.
Example 08:
- Find the combined equation of the lines whose separate equations are 2x + y = 0 and 3x – 5y = 0.
- Solution:
Given equations of lines are 2x+y = 0 and 3x-5y = 0
(2x+y )(3x-5y) = 0
∴ 2x(3x-5y) + y(3x-5y) = 0
∴ 6x² – 10xy + 3xy – 5y² = 0
∴ 6x² – 7xy – 5y² = 0
This is the required combined equation.
Example 09:
- Find the combined equation of the lines whose separate equations are x + 2y – 1 = 0 and 2x – 3y + 2 = 0.
- Solution:
Given equations of lines are x + 2y – 1 = 0 and 2x – 3y + 2 = 0.
(x + 2y – 1 )(2x – 3y + 2) = 0
∴ x(2x – 3y + 2) + 2y(2x – 3y + 2) – 1(2x – 3y + 2) = 0
∴ 2x² – 3xy + 2x + 4xy – 6y² + 4y – 2x + 3y – 2 = 0
∴ 2x² + xy – 6y² + 7y – 2 = 0
This is the required combined equation.