Condition That Line is Represented by Homogeneous Equation

Science > Mathematics > Pair of Straight Lines > Condition That Line is Represented by Homogeneous Equation

In this article, we shall study problems to find the condition when one of the lines represented by a homogeneous equation is given.

ALGORITHM :

• Write the auxiliary equation of joint equation.
• Find the slope of given line m.
• Substitute value of m in auxillary equation.
• Simplify and get the condition.

Example – 01:

• If the joint equation of lines is ax² + 2hxy  + by² = 0. Find the condition that the line 5x + 3y = 0 is one of them.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

One of the line is 5x + 3y = 0. Its slope is – 5/3

Now – 5/3 must be one of the roots of the auxiliary equation (1),

Substituting m = – 5/3 in equation (1)

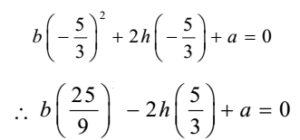
Multiplying both sides of the equation by 9

25 b -15 h + 9a = 0

9a + 25 b -15 h  = 0

This is the required condition.

Example – 02:

• If the joint equation of lines is  ax² + 2hxy  + by² = 0. Find the condition that the line 3x – y = 0 is one of them.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

One of the line is 3x – y = 0. Its slope is – 3/-1 = 3

Now 3 must be one of the roots of the auxiliary equation (1),

b(3)² + 2h(3) + a = 0

∴   9b + 6h + a = 0

∴   a + 9b + 6h = 0

This is the required condition.

Example – 03:

• If the joint equation of lines is ax² + 2hxy  + by² = 0. the line 4x – 3y = 0 coincides with one of them. Show that   16 b + 24 h + 9a = 0.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

One of the line is 4x – 3y = 0. Its slope is – 4/-3 = 4/3

Now 3 must be one of the roots of the auxiliary equation (1),

b(4/3)² + 2h(4/3) + a = 0

∴  b(16/9) + 2h(4/3) + a = 0

Multiplying both sides of the equation by 9

16b + 24 h + 9a = 0, Proved as required.

Example – 04:

• Find the condition that one of the line represented by ax² + 2hxy  + by² = 0 is y = mx
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

One of the line is y = mx . Its slope is m

Now m must be one of the roots of the auxiliary equation (1),

b(m)² + 2h(m) + a = 0

∴  bm² + 2hm + a = 0

This is the required condition..

Example – 05:

• Find the condition that one of the line represented by ax² + 2hxy  + by² = 0 is px + qy = 0.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

One of the line is px + qy = 0. Its slope is – p/q

Now – p/q must be one of the roots of the auxiliary equation (1),

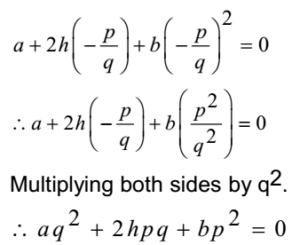
This is the required condition

Example – 06:

• Find the condition that one of the line represented by ax² 2hxy  + by² = 0. is 3x – 2y = 0
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

One of the line is 3x – 2y = 0. Its slope is – 3/-2 = 3/2

Now 3/2 must be one of the roots of the auxiliary equation (1),

b(3/2)² + 2h(3/2) + a = 0

∴  b(9/4) + 2h(3/2) + a = 0

Multiplying both sides of the equation by 4

9b + 12 h + 4a = 0

This is the required condition

 Example – 07:

• Find the condition that the line 4x + 5y = 0 coincides with one of the line represented by ax² + 2hxy  + by² = 0. OR  If the line 4x + 5y = 0 coincides with one of the line epresented by ax² + 2hxy  + by² = 0, prove that 25a – 40h + 16 b = 0.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

One of the line is 4x + 5y = 0. Its slope is – 4/5

Now – 4/5 must be one of the roots of the auxiliary equation (1),

b(-4/5)² + 2h(-4/5) + a = 0

∴  b(16/25) + 2h(-4/5) + a = 0

Multiplying both sides of the equation by 25

16b – 40 h + 25a = 0

25a – 40h + 16 b = 0. Proved as required

Example – 08:

• If the joint equation of lines is ax² + 2hxy  + by² = 0. Find the condition that the line 3x + 4y = 7 is perpendicular to one of them.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

Given line is 3x + 4y = 7. Its slope is – 3/4

As one of the lines is perpendicular to given line

Hence slope of one of the line represented by joint equation is 4/3

Now 4/3 must be one of the roots of the auxiliary equation (1),

b(4/3)² + 2h(4/3) + a = 0

∴  b(16/9) + 2h(4/3) + a = 0

Multiplying both sides of the equation by 9

16b + 24h + 9a = 0

9a + 16b + 24h = 0

This is the required condition

Example – 09:

• If the joint equation of lines is ax² + 2hxy  + by² = 0. Find the condition that the line x + 2y = 0 is perpendicular to one of them.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

Given line is x + 2y = 0. Its slope is – 1/2

As one of the lines is perpendicular to given line

Hence slope of one of the line represented by joint equation is 2

Now 2 must be one of the roots of the auxiliary equation (1),

b(2)² + 2h(2) + a = 0

4b + 4h + a = 0

a + 4b + 4h = 0

This is the required condition

Example – 10:

• If the joint equation of lines is ax² + 2hxy  + by² = 0. Find the condition that the line 3x + y = 0 is perpendicular to one of them.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

Given line is 3x + y = 0. Its slope is – 3/1 = -3

As one of the lines is perpendicular to given line

Hence slope of one of the line represented by joint equation is 1/3

Now 1/3 must be one of the roots of the auxiliary equation (1),

b(1/3)² + 2h(1/3) + a = 0

b(1/9) + 2h(1/3) + a = 0

Multiplying both sides by 9

b + 6h + 9a = 0

9a + b + 6h = 0

This is the required condition

Example – 11:

• If the joint equation of lines is ax² + 2hxy  + by² = 0. Find the condition that the line px + qy = 0 is perpendicular to one of them.
• Solution:

Given joint equation of lines is ax² + 2hxy  + by² = 0.

Its auxiliary equation is

bm² + 2hm + a = 0  ……… (1)

Given line is px + qy = 0. Its slope is – p/q

As one of the lines is perpendicular to given line

Hence slope of one of the line represented by joint equation is q/p

Now q/p must be one of the roots of the auxiliary equation (1),

b(q/p)² + 2h(q/p) + a = 0

b(q²/p²) + 2h(q/p) + a = 0

Multiplying both sides by p²

bq² + 2pqh + ap² = 0

ap² + bq² + 2pqh = 0

This is the required condition

Science > Mathematics > Pair of Straight Lines > Condition That Line is Represented by Homogeneous Equation