Distance Formula

In this article, we shall study to find the distance between two points using the distance formula when the coordinates of the two points are given.

Example 01:

• Find the distance between the following pairs of points :
• (2, 3), (4, 1)

Let A(2, 3) ≡ (x₁, y₁) and B(4, 1) ≡ (x₂, y₂) be the points

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  AB² = (4 – 2)² + (1 – 3)²  = (2)² + (-2)² = 4 + 4 = 8

∴  AB =√8  = 2√2 unit

Ans: The distance between given points is 2√2 unit

• (– 5, 7), (– 1, 3)

Let A(-5, 7) ≡ (x₁, y₁) and B(-1, 3) ≡ (x₂, y₂) be the points

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  AB² = (-1 + 5)² + (3 – 7)²  = (4)² + (-4)² = 16 + 16 = 32

∴  AB =√32  = 4√2 unit

Ans: The distance between given points is 4√2 unit

• (6, 8), (– 9, – 12)

Let A(6, 8) ≡ (x₁, y₁) and B(-9, -12) ≡ (x₂, y₂) be the points

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  AB² = (- 9 – 6)² + (-12 – 8)²  = (-15)² + (-20)² = 225 + 400 = 625

∴  AB =√625  = 25 unit

Ans: The distance between given points is 25 unit

• (-6, -1), (– 6, 11)

Let A(-6, -1) ≡ (x₁, y₁) and B(-6, 11) ≡ (x₂, y₂) be the points

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  AB² = (- 6 + 6)² + (11 + 1)²  = (0)² + (12)² = 0 + 144 = 144

∴  AB =√144  = 12 unit

Ans: The distance between given points is 12 unit

• (a, b), (– a, – b)

Let A(a, b) ≡ (x₁, y₁) and B(-a, -b) ≡ (x₂, y₂) be the points

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  AB² = (- a – a)² + (-b – b)²  = (- 2a)² + (- 2b)² = 4a² + 4b² = 4(a² + 4b²)

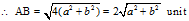
• (0, 0), (36, 15)

Let A(0, 0) ≡ (x₁, y₁) and B(36, 15) ≡ (x₂, y₂) be the points

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  AB² = (36 – 0)² + (15 – 0)²  = (36)² + (15)² = 1296 + 225 = 1521

∴  AB =√1521  = 39 unit

Alternate Direct Method

One of the given point is origin O. Let A(36, 15) ≡ (x, y)

∴  OA² = x² + y² = (36)² + (15)²  = 1296 + 225 = 1521

∴  OA =√1521  = 39 unit

Ans: The distance between given points is 39 unit

Example 02:

• Using distance formula show that following sets of points are collinear
• A(0,4), B(2,10) and C(3,13)

Given points are A(0,4), B(2,10) and C(3,13)

Using distance formula

AB² = (2 – 0)² + (10 – 4)² = (2)² + (6)² = 4 + 36 = 40

∴  AB  = √40  =  2√10  unit …………….. (1)

BC² = (3 – 2)² + (13 – 10)² = (1)² + (3)² = 1 + 9 = 10

∴  BC  = √10   unit  …………….. (2)

AC² = (3 – 0)² + (13 – 4)² = (3)² + (9)² = 9 + 81 = 90

∴  AC  = √90  =  3√10  unit …………….. (3)

From equations (1), (2) and (3) we have

AC = AB + BC

∴ A – B – C

Hence points A, B and C are collinear

• P(5, 0), Q(10, -3) and R(-5, 6)

Given points are P(5, 0), Q(10, -3) and R(-5, 6)

Using distance formula

PQ² = (10 – 5)² + (-3 – 0)² = (5)² + (-3)² = 25 + 9 = 34

∴  PQ  = √34   unit   …………….. (1)

QR² = (-5 – 10)² + (6 + 3)² = (-15)² + (9)² = 225 + 81 = 306

∴  QR  = √306  =  3√34   unit …………….. (2)

PR² = (-5 – 5)² + (6 – 0)² = (-10)² + (6)² = 100+ 36 = 136

∴  PR  = √136  =  2√34   unit …………….. (3)

From equations (1), (2) and (3) we have

QR = PQ + PR

∴ Q – P – R

Hence points P, Q and R are collinear

• L(2, 5), M(5, 7) and N(8, 9)

Given points are L(2, 5), M(5, 7) and N(8, 9)

Using distance formula

LM² = (5 – 2)² + (7 – 5)² = (3)² + (2)² = 9 + 4 = 13

∴  LM  = √13   unit   …………….. (1)

MN² = (8 – 5)² + (9 – 7)² = (3)² + (2)² = 9 + 4 = 13

∴  MN  = √13  unit …………….. (2)

LN² = (8 – 2)² + (9 – 5)² = (6)² + (4)² = 36+ 16 = 52

∴  LN  = √52  =  2√13   unit …………….. (3)

From equations (1), (2) and (3) we have

LN = LM + MN

∴ L – M – N

Hence points L, M and N are collinear

• D(5, 1), E(1, -1) and F(11, 4)

Given points are D(5, 1), E(1, -1) and F(11, 4)

Using distance formula

DE² = (1 – 5)² + (-1 – 1)² = (-4)² + (-2)² = 16 + 4 = 20

∴  DE  = √20  =  2√5   unit   …………….. (1)

EF² = (11 – 1)² + (4 + 1)² = (10)² + (5)² = 100 + 25 = 125

∴  EF  = √125 =  5√5  unit …………….. (2)

DF² = (11 – 5)² + (4 – 1)² = (6)² + (3)² = 36+ 9 = 45

∴  DF  = √45  =  3√5  unit …………….. (3)

From equations (1), (2) and (3) we have

EF = DE + DF

∴ E – D – F

Hence points D, E and F are collinear

• A(1, 5), B(2, 3) and C(– 2, – 11)

Given points are A(1, 5), B(2, 3) and C(-2, -11)

Using distance formula

AB² = (2 – 1)² + (3 – 5)² = (1)² + (-2)² = 1 + 4 = 5

∴  AB  = √5   unit …………….. (1)

BC² = (-2 – 2)² + (-11 – 3)² = (-4)² + (-14)² = 16 + 196 = 212

∴  BC  = √212    unit  …………….. (2)

AC² = (-2 – 1)² + (-11 – 5)² = (-3)² + (-16)² = 9 + 256 = 265

∴  AC  = √265    unit …………….. (3)

From equations (1), (2) and (3) we have

AC ≠ AB + BC

Hence points A, B and C are not collinear

Example 03:

• Ashima, Bharti, and Camella are seated at A(3, 1), B(6, 4), and C(8, 6) respectively. Do you think they are seated in a line?

Given points are A(3, 1), B(6, 4) and C(8, 6)

Using distance formula

AB² = (6 – 3)² + (4 – 1)² = (3)² + (3)² = 9 + 9 = 18

∴  AB  = √18  = 3√2 unit …………….. (1)

BC² = (8 – 6)² + (6 – 4)² = (2)² + (2)² = 4 + 4 = 8

∴  BC  = √8  = 2√2   unit  …………….. (2)

AC² = (8 – 3)² + (6 – 1)² = (5)² + (5)² = 25 + 25 = 50

∴  AC  = √50   = 5√2  unit …………….. (3)

From equations (1), (2) and (3) we have

AC = AB + BC

∴ A – B – C

Hence points A, B and C are collinear.

Thus Ashima, Bharti and Camella are seated in a line

Example 04:

• The distance between the points (0, 0) and (x, 3) is 5. Find x.

Let A(0, 0) ≡ (x₁, y₁) and B(x, 3) ≡ (x₂, y₂) be the points.

Thus AB = 5

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  5² = (x – 0)² + (3 – 0)²  = x² + 9

∴   25 = x² + 9

∴  x² = 16

∴  x = ± 4

Example 05:

• The distance between the points (a, 5) and (0, -3) is 4√5  unit. Find a.

Let A(a, 5) ≡ (x₁, y₁) and B(0, -3) ≡ (x₂, y₂) be the points.

Thus AB = 4√5

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  (4√5)² = (0 – a)² + (-3 – 5)²  = (-a)² + (-8)² = a² + 64

∴  80 =  a² + 64

∴  a² = 16

∴  a = ± 4

Example 06:

• The distance between the points (8, -7) and (-4, a) is 13. Find a.

Let A(8, -7) ≡ (x₁, y₁) and B(-4, a) ≡ (x₂, y₂) be the points.

Thus AB = 5

By distance formula

AB² = (x₂ – x₁)² + (y₂ – y₁)²

∴  13² = (- 4 – 8)² + (a + 7)²  = (-12)² + a² + 14a + 49

∴  169 =  144 + a² + 14a + 49

∴  a² + 14a + 197 – 169 = 0

∴  a² + 14a + 24 = 0

∴  (a + 12)(a + 2) = 0

∴  a + 12 = 0 or a + 2 = 0

∴  a = -12 and a = -2

Example 07:

• Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.

Given P(2, -3) ≡ (x₁, y₁) and Q(10, y) ≡ (x₂, y₂) be the points.

Thus PQ = 10 units

By distance formula

PQ² = (x₂ – x₁)² + (y₂ – y₁)²

∴  10² = (10 – 2)² + (y + 3)²  = (8)² + y² + 6y + 9

∴  100 = 64 + y² + 6y + 9

∴  36 =  y² + 6y + 9

∴  y² + 6y + 9 – 36 = 0

∴  y² + 6y + – 27 = 0

∴  (y + 9)(y – 3) = 0

∴  y + 9 = 0 or y – 3 = 0

∴  y = -9 and y = 3

Example 08:

• Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).

Let P(2, –5) and Q(–2, 9) be the given points.

Let the point on the x-axis be A(a, 0)

Given PA = QA

PA² = QA²

Using distance formula

(a – 2)² + (0 + 5)² = (a + 2)² + (0 – 9)²

∴  a² – 4a + 4 + 25  = a² + 4a + 4 + 81

∴   – 4a + 25  = + 4a + 81

∴   – 8a =  56

∴  a = – 7

Hence the required point is (-7, 0)

Example 09:

• Find a point on the y-axis which is equidistant from points A(6, 5) and B(– 4, 3).

A(6, 5) and B(– 4, 3) are given points.

Let the point on the y-axis be P(0, b)

Given PA = PB

PA² = PB²

Using distance formula

(0 – 6)² + (b – 5)² = (0 + 4)² + (b – 3)²

∴  36 + b² – 10 b + 25  = 16 + b² – 6b + 9

∴  36  – 10 b + 25  = 16  – 6b + 9

 ∴  – 4b =  25 – 61 = -36

∴  b = 9

Hence the required point is (0, 9)

Example 10:

• Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4)

Let P(3, 6) and Q(–3, 4) be the given points.

Given point A(x, y)

Given PA = QA

PA² = QA²

Using distance formula

(x – 3)² + (y – 6)² = (x + 3)² + (y – 4)²

∴  x² – 6x + 9 + y² – 12y + 36  = x² + 6x + 9 + y² – 8y + 16

∴  x² – 6x + 9 + y² – 12y + 36  – x² – 6x – 9 – y² + 8y – 16 = 0

∴   – 12x – 4y + 20  = 0

∴  3x + y – 5 = 0

Hence the requiredrelation is 3x + y – 5 = 0

Example 11:

• Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).

Let P(7, 1) and Q(3, 5) be the given points.

Given point A(x, y)

Given PA = QA

PA² = QA²

Using distance formula

(x – 7)² + (y – 1)² = (x – 3)² + (y – 5)²

∴  x² – 14x + 49 + y² – 2y + 1  = x² – 6x + 9 + y² – 10y + 25

∴  x² – 14x + 49 + y² – 2y + 1  – x² + 6x – 9 – y² + 10y – 25 = 0

∴   – 8x + 8y + 16  = 0

∴  x – y + 2 = 0

Hence the requiredrelation is x – y + 2 = 0

Example 12:

• If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also, find the distances QR and PR.

Given P(5, -3) and R(x, 6) be the given points.

Given point Q(0, 1)

Given PQ = RQ

PQ² = RQ²

Using distance formula

(5 – 0)² + (-3 – 1)² = (x – 0)² + (6 – 1)²

∴  (5)² + (-4)² = (x)² + (5)²

∴  25 + 16 = x² + 25

∴  x²  = 16

∴  x = ± 4

When R(4, -3)

QR² = (4 – 0)² + (-3 – 1)² = (4)² + (-4)² = 16 + 16 = 32

∴  QR  = √32  =  4√2   unit   …………….. (1)

PR² = (4 – 5)² + (-3 + 3)² = (-1)² + (0)² = 1 + 0 = 1

∴  PR  = √1  =  1   unit   …………….. (1)

When R(-4, -3)

QR² = (-4 – 0)² + (-3 – 1)² = (-4)² + (-4)² = 16 + 16 = 32

∴  QR  = √32  =  4√2   unit   …………….. (1)

PR² = (-4 – 5)² + (-3 + 3)² = (-9)² + (0)² = 81 + 0 = 81

∴  PR  = √81  =  9   unit   …………….. (1)

Example 13:

• If P (6, -1), Q(1, 3), and R(x, 8) are the points and PQ = QR,  find the values of x.

Given P(6, -1) and R(x, 8) be the given points.

Given point Q(1, 3)

Given PQ = RQ

PQ² = RQ²

Using distance formula

(1 – 6)² + (3 + 1)² = (1 – x)² + (3 – 8)²

∴  (-5)² + (-4)² = x² – 2x + 1 + (-5)²

∴  25 + 16 = x² – 2x + 1 +25

∴  x²  – 2x + 1 – 16 = 0

∴  x²  – 2x + – 15 = 0

∴  (x + 3)(x – 5) = 0

∴ x + 3 = 0 and x – 5 = 0

∴ x = – 3 and x = 5