Equation of Circle (Centre Radius Form)

A circle is defined as the locus of all the points in a plane, which are at a fixed distance from a fixed point. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle. The radius of a circle is denoted by the letter ‘r’ or ‘R’. In this article, we shall study, the equation of a circle in the centre radius form.

Standard Equation of Circle:

By distance formula

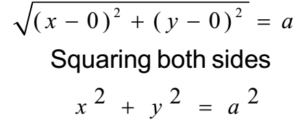
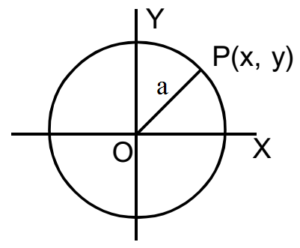
Let P(x, y) be any point on a circle having centre at O(0, 0) and radius ‘a’.
Then, OP = radius of a circle = a
By distance formula
As this contains less number of constants, the equation is called the standard equation of a circle.

Centre Radius Form:

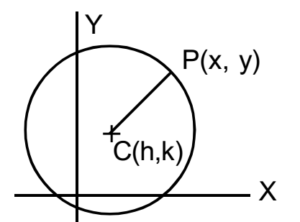
By distance formula

Let P(x, y) be any point on a circle having centre at C(h, k) and radius ‘r’.
Then, CP = radius of a circle = r
By distance formula
This form of the equation of a circle is called centre radius form.

Equation of Circle When Centre and Radius are Given

Algorithm:

1. Write given centre ≡ (h, k) and given radius = r
2. Use centre radius form (x – h)² + (y – k)² = r²
3. Simplify the equation and write it in standard form ax² + by² + 2gx + 2fy + c = 0

Example – 01:

• Find the equation of circle having centre at (2, -3) and radius 5.
• Solution:

Given centre (2, -3) ≡ (h, k) and radius = r = 5

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x – 2)² + (y + 3)² = 5²

∴  x² – 4x + 4 + y² + 6y + 9 = 25

∴  x² + y² – 4x + 6y + 13 – 25 = 0

∴  x² + y² – 4x + 6y – 12 = 0

Ans: The required equation of circle is x² + y² – 4x + 6y – 12 = 0

Example – 02:

• Find equation of circle having centre at origin and radius 4.
• Solution:

Given centre (0, 0) ≡ (h, k) and radius = r = 4

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x – 0)² + (y + 0)² = 4²

∴  x²  + y² = 16

Ans: The required equation of circle is x² + y²  = 16

Example – 03:

• Find the equation of circle having centre at (3, -2) and radius 5.
• Solution:

Given centre (3, -2) ≡ (h, k) and radius = r = 5

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x – 3)² + (y + 2)² = 5²

∴  x² – 6x + 9 + y² + 4y + 4 = 25

∴  x² + y² – 6x + 4y + 13 – 25 = 0

∴  x² + y² – 6x + 4y – 12 = 0

Ans: The required equation of circle is x² + y² – 6x + 4y – 12 = 0

Example – 04:

• Find the equation of circle having centre at (-3, -2) and radius 6.
• Solution:

Given centre (-3, -2) ≡ (h, k) and radius = r = 6

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x + 3)² + (y + 2)² = 6²

∴  x² + 6x + 9 + y² + 4y + 4 = 36

∴  x² + y² + 6x + 4y + 13 – 36 = 0

∴  x² + y² + 6x + 4y – 23 = 0

Ans: The required equation of circle is x² + y² + 6x + 4y  – 23 = 0

Example – 05:

• Find the equation of circle having centre at (a cosα, a sinα) and radius a.
• Solution:

Given centre (a cosα, a sinα) ≡ (h, k) and radius = r = 6

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

(x – a cosα)² + (y – a sinα)² = a²

∴  x² – 2xa cosα + a² cos²α + y² – 2ya sinα + a² sin²α = a²

∴  x² + y²  – 2ax cosα  – 2ay sinα + a² cos²α  + a² sin²α = a²

∴  x² + y²  – 2ax cosα  – 2ay sinα + a² (cos²α  + sin²α) – a²  = 0

∴  x² + y²  – 2ax cosα  – 2ay sinα + a² (1) – a²  = 0

∴  x² + y²  – 2acosα.x  – 2a sinα.y = 0

Ans: The required equation of circle is x² + y²  – 2acosα.x  – 2a sinα.y = 0

Example – 06:

• Find the equation of circle having centre at (a, b) and radius  √a²+b²
• Solution:

Given centre (a, b) ≡ (h, k) and radius = r = √a²+b² 

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x – a)² + (y – b)² = (√a²+b²  )²

∴  x² – 2ax + a² + y² – 2by + b² = a² + b²

∴  x² + y² – 2ax – 2by + a²  + b² – a² – b² = 0

∴  x² + y² – 2ax – 2by  = 0

Ans: The required equation of circle is x² + y² – 2ax – 2by  = 0

Equation of Circle When Centre and Point on the Circle are Given:

Algorithm:

1. Write given centre C ≡ (h, k) and given point say P (x, y)
2. Use distance formula to find CP represent it as radius = r
3. Use centre radius form (x – h)² + (y – k)² = r²
4. Simplify the equation and write it in standard form ax² + by² + 2gx + 2fy + c = 0

Example 07:

• Find the equation of circle having centre at (-3, 1) and passing through (5, 2)
• Solution:

Given centre C(-3, 1) ≡ (h, k) and  point on circle P(5, 2)

By distance formula

CP² = (5 + 3)² + (2 – 1)² = 64 + 1 = 65

∴  CP = √65

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x + 3)² + (y – 1)² = (√65)²

∴  x² + 6x + 9 + y² – 2y + 1 = 65

∴  x² + y² + 6x – 2y + 10 – 65 = 0

∴  x² + y² + 6x – 2y – 55 = 0

Ans: The required equation of circle is x² + y² + 6x – 2y – 55 = 0

Example 08:

• Find the equation of circle having centre at (2, -1) and passing through (3, 6)
• Solution:

Given centre C(2, -1) ≡ (h, k) and  point on circle P(3, 6)

By distance formula

CP² = (3 – 2)² + (6 + 1)² =1 + 49 = 50

∴  CP = √50

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x – 2)² + (y + 1)² = (√50)²

∴  x² – 4x + 4 + y² + 2y + 1 = 50

∴  x² + y² – 4x + 2y + 5 – 50 = 0

∴  x² + y² – 4x + 2y – 45 = 0

Ans: The required equation of circle is x² + y² – 4x + 2y – 45 = 0

Example 09:

• Find the equation of circle having centre at (2, -3) and passing through P(-3, 5)
• Solution:

Given centre C(2, – 3) ≡ (h, k) and  point on circle (-3, 5)

By distance formula

CP² = (-3 – 2)² + (5 + 3)² = 25 + 68 = 89

∴  CP = √89

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x – 2)² + (y + 3)² = (√89)²

∴  x² – 4x + 4 + y² + 6y + 9 = 89

∴  x² + y² – 4x + 6y + 13 – 89 = 0

∴  x² + y² – 4x + 6y – 76 = 0

Ans: The required equation of circle is x² + y² – 4x + 6y – 76 = 0

Example 10:

• Find equation of circle passing through (-3, 2) and having centre at the point of intersection of lines x – 2y = 4 and 2x + 5y + 1 = 0
• Solution:

Solving the equations x – 2y = 4 and 2x + 5y + 1 = 0 we get x = 2 and y = -1

Thus centre C(2, – 1) ≡ (h, k) and  point on circle P(-3, 2)

By distance formula

CP² = (-3 – 2)² + (2 + 1)² = 25 + 9 = 34

∴  CP = √34

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x – 2)² + (y + 1)² = (√34)²

∴  x² – 4x + 4 + y² + 2y + 1 = 34

∴  x² + y² – 4x + 2y + 5 – 34 = 0

∴  x² + y² – 4x + 2y – 29 = 0

Ans: The required equation of circle is x² + y² – 4x + 2y – 29 = 0

Example 11:

• Find equation of circle passing through intersection of x + 3y = 0 and 2x – 7y = 0 and having centre at the point of intersection of lines x + y + 1 = 0 and x – 2y + 4 = 0
• Solution:

Solving the equations x + 3y = 0 and 2x – 7y = 0 we get x = 0 and y = 0

Hence the circle passes through O(0, 0)

Solving the equations x + y + 1 = 0 and x – 2y + 4 = 0 we get x = -2 and y = 1

Hence the centre of circle is C(-2, 1)

Thus centre C(-2, 1) ≡ (h, k) and  point on circle O(0, 0)

By distance formula

CO² = (0 + 2)² + (0 – 1)² = 4 + 1 = 5

∴  CO = √5

By centre radius form, the equation of circle is given by

(x – h)² + (y – k)² = r²

∴  (x + 2)² + (y – 1)² = (√5)²

∴  x² + 4x + 4 + y² – 2y + 1 = 5

∴  x² + y² + 4x – 2y + 5 – 5 = 0

∴  x² + y² + 4x – 2y = 0

Ans: The required equation of circle is x² + y² + 4x – 2y = 0

Find equation of a circle having centre at (- 4, 0) and radius 5. Ans: x2 + y2 + 8x – 34 = 0
6. Find equation of a circle having centre at (7, 2) and radius 3. Ans: x2 + y2 – 14x – 4y + 44 = 0
7. Find equation of a circle having centre at (- 5, 1) and radius 2. Ans: x2 + y2 + 10x – 2y + 14 = 0
8. Find equation of a circle having centre at (1, -1) and passing through (3, 2) (M – 78)
Ans: x2 + y2 – 2x + 2y – 11 = 0
9. Find equation of a circle having centre at (2, -1) and passing through (5, 3) (O – 81)
Ans: x2 + y2 – 4x + 2y – 20 = 0.
10. Find equation of a circle having centre at (2, -3) and passing through (-1, 2) (M – 98)
Ans: x2 + y2 – 4x + 6y – 21 = 0
11. Find equation of a circle having centre at (1, -2) and passing through intersection of lines 3x + y = 14 and 2x + 5y = 18. Ans: x2 + y2 – 2x + 4y – 20 = 0
12. Find equation of a circle having centre at (- 4, 3) and Y – axis is tangent to it. (O – 78)
Ans: x2 + y2 + 8x – 6y + 9 = 0
13. Find equation of a circle having centre at (2, – 6) and touching X – axis.
Ans: x2 + y2 – 4x+ 12y + 4 = 0
14. Find equation of a circle having centre at (2, 3) and touching X – axis.
Ans: x2 + y2 – 4x – 6y + 4 = 0
15. Find equation of a circle having centre at (7, – 2) and touching X – axis.
Ans: x2 + y2 – 14x + 4y + 49 = 0
16. Find equation of a circle which touches X – axis at (-1, 0) and have radius 5.
Ans: