Equation of Locus: Set – I

Science > Mathematics > Coordinate Geometry > Locus > Equation of Locus

In this article, we shall study the concept of locus and to find the equation of the locus.

Locus: A set of points satisfying some geometrical condition or conditions is called as the locus

For example, a circle is a locus of all the points in the plane which are equidistant from the point in the plane.

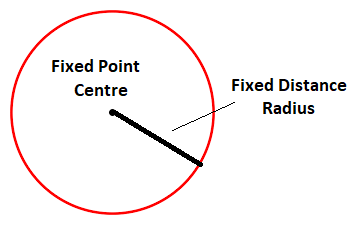
Equation of Locus: The equation of locus is an equation which is satisfied by all the points satisfying given the geometrical condition in the problem

Steps Involved in Finding Equation of Locus:

1. Assume the locus point P(x, y)
2. Write  given geometrical condition
3. Use distance, section, centroid, and other formulae as per condition
4. Substitute in geometrical condition. Simplify to get the equation of locus

Example – 01:

Find the locus of a point P such that its ordinate is 5.

Solution:

Let P(x. y) be the point on the locus

Given ordinate of P is  5 i.e. y = 5

Hence required equation of the locus of point P is y = 5.

Example – 02:

Find the locus of a point P such that its abscissa is 3.

Solution:

Let P(x. y) be the point on the locus

Given abscissa of P  is  3 i.e. x = 3

Hence required equation of the locus of point P is y = 3

Example – 03:

Find the locus of a point P such that its ordinate is equal to the abscissa.

Solution:

Let P(x. y) be the point on the locus

Given ordinate of P is equal to the abscissa

Hence required equation of the locus of point P is y = x  or x – y = 0

Example – 04:

Find the locus of a point P such that its ordinate exceeds 5 times its abscissa by 9

Solution:

Let P(x. y) be the point on the locus

Given ordinate of P exceeds 5 times its abscissa by 9

Hence required equation of the locus of point P is y = 5x + 9.

Example – 05:

Find the locus of a point P such that its abscissa exceeds 2 times its abscissa by 3

Solution:

Let P(x. y) be the point on the locus

Given abscissa of P exceeds 2 times its abscissa by 3

Hence required equation of the locus of point P is x = 2y + 3.

Example – 06:

Find the locus of a point P such that the sum of its coordinates is 15

Solution:

Let P(x. y) be the point on the locus

Given the sum of its coordinates is 15

Hence required equation of the locus of point P is x + y = 15

Example – 07:

Find the locus of a point P such that the sum of its coordinates is 10

Solution:

Let P(x. y) be the point on the locus

Given the sum of  its coordinates is 10

Hence required  inequality of the locus of point P is x + y = 10

Example – 08:

Find the locus of a point P such that the sum of its coordinates is less than 10

Solution:

Let P(x. y) be the point on the locus

Given the sum of its coordinates is less than 10

Hence required  inequality of the locus of point P is x + y < 10

Example – 09:

Find the locus of a point P such that the sum of its coordinates is greater than 5

Solution:

Let P(x. y) be the point on the locus

Given the sum of its coordinates is greater than 5

Hence required  inequality of the locus of point P is x + y > 5

Example – 10:

Find the locus of a point P such that the sum of squares of  its coordinates is 25

Solution:

Let P(x. y) be the point on the locus

Given the sum of squares of  its coordinates is 25

Hence required equation of the locus of point P is x² + y² = 25

Example – 11:

Find the locus of a point P such that the sum of square its coordinates is 9

Solution:

Let P(x. y) be the point on the locus

Given the sum of square of its coordinates is 9

Hence required  inequality of the locus of point P is x² + y² = 9

Example – 12:

Find the locus of a point P such that twice the ordinate of P exceeds thrice its abscissa by 4.

Solution:

Let P(x. y) be the point on the locus

Given twice the ordinate of P exceeds thrice its abscissa by 4.

Hence required equation of the locus of point P is 2y = 3x + 4

Example – 13:

Find the locus of a point P such that the distance of P from x-axis equal to 10 times its distance from the y-axis.

Solution:

Let P(x. y) be the point on the locus

Distance from x-axis = y

Distance from y-axis = x

Given the distance of P from x-axis equal to 10 times its distance from y-axis

Hence required equation of the locus of point P is y = 10x

Example – 14:

Find the locus of a point P such that the distance of P from x-axis equal to its distance from the y-axis.

Solution:

Let P(x. y) be the point on the locus

Distance from x-axis = y

Distance from y-axis = x

Given the distance of P from x-axis equal to its distance from y-axis

Hence required equation of the locus of point P is y = x

Example – 15:

Find the locus of a point P such that the distance of P from origin equals 5 times its distance from the point (3, -2)

Solution:

Let P(x. y) be the point on the locus, Let O(0, 0) be the origin and A(3, -2) be the point

Given OP = 5 PA

∴ OP² = 25 PA²

∴ (x – 0)²  + (y – 0)²  = 25[(x – 3)²  + (y + 2)²]

∴ x²  + y²  = 25[x² – 6x + 9  + y² + 4y + 4]

∴ x²  + y²  = 25x² – 150x + 225  + 25y² + 100y + 100

∴  25x² – 150x + 225  + 25y² + 100y + 100 – x²  – y²  = 0

∴  24x² + 24y² – 150x + 100y + 325  = 0

Hence required equation of the locus  is 24x² + 24y² – 150x + 100y + 325  = 0

Example – 16:

Find the equation of locus of a point which is equidistant from the points (2, 3) and (-4, 5)

Solution:

Let P(x. y) be the point on the locus, Let A(2, 3) and B(-4, 5) be the given points

Given PA = PB

∴ PA² = PB²

∴ (x – 2)²  + (y – 3)²  = (x + 4)²  + (y – 5)²

∴ x²  – 4x + 4 + y²  -6y + 9 = x² + 8x + 16  + y² – 10y + 25

∴ x²  – 4x + 4 + y²  -6y + 9 – x² – 8x – 16  – y² + 10y – 25 = 0

∴ – 12x   + 4y  -28 = 0

∴ 3x   – y  + 7 = 0

Hence required equation of the locus  is 3x   – y  + 7 = 0

Example – 17:

Find the equation of locus of a point which is equidistant from the points (1, 2) and (3, 4)

Solution:

Let P(x. y) be the point on the locus, Let A(1, 2) and B(3, 4) be the given points

Given PA = PB

∴ PA² = PB²

∴ (x – 1)²  + (y – 2)²  = (x – 3)²  + (y – 4)²

∴ x²  – 2x + 1 + y²  – 4y + 4 = x² – 6x + 9  + y² – 8y + 16

∴ x²  – 2x + 1 + y²  -4y + 4 – x² + 6x – 9  – y² + 8y – 16 = 0

∴ – 2x + 1 -4y + 4 + 6x – 9 + 8y – 16 = 0

∴ 4x   + 4y  – 20 = 0

∴ x   + y  – 5 = 0

Hence required equation of the locus  is x   + y  – 5 = 0

Example – 18:

Find the equation of locus of a point which is equidistant from the points (2, 3) and (5, 7)

Solution:

Let P(x. y) be the point on the locus, Let A(2, 3) and B(5, 7) be the given points

Given PA = PB

∴ PA² = PB²

∴ (x – 2)²  + (y – 3)²  = (x – 5)²  + (y – 7)²

∴ x²  – 4x + 4 + y²  – 6y + 9 = x² – 10x + 25  + y² – 14y + 49

∴ x²  – 4x + 4 + y²  – 6y + 9 – x² + 10x – 25  – y² + 14y – 49 = 0

∴ 6x  +   8y  – 61 = 0

Hence required equation of the locus  is 6x  +   8y  – 61 = 0

Example – 19:

A(2, 3), B(-2, 5) are given points. Find the equation of locus of point P, such that PA = 2PB.

Solution:

Let P(x. y) be the point on the locus, Given A(2, 3) and B(-2, 5) be the given points

Given PA = 2 PB

∴ PA² = 4 PB²

∴ (x – 2)²  + (y – 3)²  = 4[(x + 2)²  + (y – 5)²]

∴ x²  – 4x + 4 + y²  – 6y + 9 = 4[ x² + 4x + 4  + y² – 10y + 25]

∴ x²  – 4x + 4 + y²  – 6y + 9 = 4 x² + 16x + 16  + 4y² – 40y + 100

∴  4 x² + 16x + 16  + 4y² – 40y + 100 – x²  + 4x – 4 – y²  + 6y – 9 = 0

∴  3 x² + 3y² + 20x – 34y + 103 = 0

Hence required equation of the locus  is 3 x² + 3y² + 20x – 34y + 103 = 0

Example – 20:

A(2, 3), B(-2, 1) are given points. Find the equation of locus of point P, such that AP² = 3 BP².

Solution:

Let P(x. y) be the point on the locus, Given A(2, 3) and B(-2, 1) be the given points

Given AP² = 3 BP²

∴ (x – 2)²  + (y – 3)²  = 3[(x + 2)²  + (y – 1)²]

∴ x²  – 4x + 4 + y²  – 6y + 9 = 3[ x² + 4x + 4  + y² – 2y + 1]

∴ x²  – 4x + 4 + y²  – 6y + 9 = 3x² + 12x + 12  + 3y² – 6y + 3

∴ 3x² + 12x + 12  + 3y² – 6y + 3 –  x²  + 4x – 4 – y²  + 6y – 9 = 0

∴ 2x² + 2y² + 16x + 2 = 0

∴ x² + y² + 8x + 1 = 0

Hence required equation of the locus  is x² + y² + 8x + 1 = 0

Example – 21:

A(3, 1), B(4, -5) are given points. Find the equation of locus of point P, such that AP²+ BP² = 50.

Solution:

Let P(x. y) be the point on the locus, Given A(3, 1) and B(4, -5) be the given points

Given AP²+ BP² = 50.

∴ (x – 3)²  + (y – 1)²  +  (x – 4)²  + (y + 5)² = 50

∴  x²  – 6x + 9 + y²  – 2y + 1 +  x² – 8x + 16  + y² + 10y + 25 = 50

∴  2x² + 2y² – 14x  + 8y + 51= 50

∴  2x² + 2y² – 14x  + 8y + 1 = 0

Hence required equation of the locus  is 2x² + 2y² – 14x  + 8y + 1 = 0

Example – 22:

A(-3, 2), B(1, -4) are given points. Find the equation of locus of point P, such that 3PA = 2 PB

Solution:

Let P(x. y) be the point on the locus, Given A(-3, 2) and B(1, -4) be the given points

Given 3 PA = 2 PB

∴ 9 PA²= 4 PB²

∴9[ (x + 3)²  + (y – 2)²]  =  4[(x – 1)²  + (y + 4)²]

∴ 9( x²  + 6x + 9 + y²  – 4y + 4) = 4(x² – 2x + 1  + y² + 8y + 16)

∴ 9 x²  + 54x + 81 + 9y²  – 36y +36 = 4x² – 8x + 4  + 4y² + 32y + 64

∴ 9 x²  + 54x + 81 + 9y²  – 36y +36 – 4x² + 8x – 4  – 4y² – 32y – 64 = 0

∴ 5x²  + 5y²  + 62x  – 68y +49 = 0

Hence required equation of the locus  is 5x²  + 5y²  + 62x  – 68y +49 = 0

Example – 23:

Find the equation perpendicular bisector of segment joining points (-5, 2) and (-1, 5)

Solution:

Let P(x. y) be the point on the locus, Let A(-5, 2) and B(-1, 5) be the given points

Perpendicular bisector of a line segment is locus of all the points

in the plane whci is equidistant from the endpoints of the segment

Hence PA = PB

∴ PA² = PB²

∴ (x + 5)²  + (y – 2)²  = (x + 1)²  + (y – 5)²

∴ x²  + 10x + 25 + y²  -4y + 4 = x² + 2x + 1 + y² – 10y + 25

∴ x²  + 10x + 25 + y²  -4y + 4 – x² – 2x – 1 – y² + 10y – 25 = 0

∴ 8x  + 6y + 3 = 0

Hence required equation of the locus (perpendicular bisector) is 3x   – y  + 7 = 0

Example – 24:

A(4, 5), B(-2, 7) are given points. Find the equation of locus of point P, such that 2PA = PB

Solution:

Let P(x. y) be the point on the locus, Given A(4, 5) and B(-2, 7) be the given points

Given 2PA = PB

∴ 4 PA²= PB²

∴4[ (x -4 )²  + (y – 5)²]  =  (x + 2)²  + (y – 7)²

∴ 4( x²  – 8x + 16 + y²  – 10y + 25) = x² + 4x + 4  + y² – 14y + 49

∴ 4x²  – 32x +64 + 4y²  – 40y + 100 = x² + 4x + 4  + y² – 14y + 49

∴ 4x²  – 32x +64 + 4y²  – 40y + 100 – x² – 4x – 4  – y² + 14y – 49 = 0

∴ 3x²  + 3y²  – 36x  – 26 y +111 = 0

Hence required equation of the locus  is 3x²  + 3y²  – 36x  – 26 y + 111 = 0

Example – 25:

Find the equation of locus of points whose distance from the point (2, -3) is twice its distance from (1, 2).

Solution:

Let P(x. y) be the point on the locus, Given A(2, -3) and B(1, 2) be the given points

Given PA = 2 PB

∴ PA²= 4 PB²

∴ (x – 2 )²  + (y + 3)²  = 4[ (x – 1)²  + (y – 2)²]

∴  x²  – 4x + 4 + y²  + 6y + 9 = 4[x² – 2x + 1  + y² – 4y + 4]

∴  x²  – 4x + 4 + y²  + 6y + 9 = 4x² – 8x + 4  + 4y² – 16y + 16

∴  4x² – 8x + 4  + 4y² – 16y + 16 –  x² + 4x – 4 – y²  – 6y – 9 = 0

∴ 3x²  + 3y²  – 4x  – 22 y + 7 = 0

Hence required equation of the locus  is 3x²  + 3y²  – 4x  – 22 y + 7 = 0

Example – 26:

Find the equation of locus of a point such that, the difference of square of its distances from the points (5, 0) and (2, 3) is 10.

Solution:

Let P(x. y) be the point on the locus, Given A(5, 0) and B(2, 3) be the given points

Given  PA² – PB² = 10

∴ [(x – 5 )²  + (y – 0)² ] –  [(x – 2)²  + (y – 3)²] = 10

∴ ( x²  – 10x + 25 + y²) – (x² – 4x + 4  + y² – 6y + 9) = 10

∴ x²  – 10x + 25 + y² – x² + 4x – 4  – y² + 6y – 9 – 10 = 0

∴  – 6x + 6y + 2 = 0

∴  3x – 3y – 1 = 0

Hence required equation of the locus  is 3x – 3y – 1 = 0

Example – 27:

Find the equation of locus of a point such that, the sum of the square of its distances from the points (2, -3) and (-1, -2) is 15.

Solution:

Let P(x. y) be the point on the locus, Given A(2, -3) and B(-1, -2) be the given points

Given  PA² + PB² = 15

∴ [(x – 2 )²  + (y + 3)² ] +  [(x + 1)²  + (y + 2)²] = 15

∴ x²  – 4x + 4 + y² + 6y + 9 + x² + 2x + 1  + y² + 4y +4 – 15 = 0

∴ 2x² + 2y²  – 2x +10y +  3 = 0

Hence required equation of the locus  is 2x² + 2y²  – 2x +10y +  3 = 0

Example – 28:

A(5, -6), B(-1, 2) and C(4, -3) are three given points. Find the equation of locus of points P such that PA² + PC² = AB².

Solution:

Let P(x. y) be the point on the locus, Given A(5, -6), B(-1, 2) and C(4, -3) be the given points

Given  PA² + PC² = AB²

∴ [(x – 5 )²  + (y + 6)² ] +  [(x – 4)²  + (y + 3)²] = (-1 – 5)² + (2 + 6)²

∴ x²  – 10x + 25 + y² + 12y + 36 + x² – 8x + 16  + y² + 6y +9 = 36 + 64

∴ 2x²  + 2 y² – 18x + 18 y – 14 = 0

∴ x²  + y² – 9x + 9y – 7 = 0

Hence required equation of the locus  is x²  + y² – 9x + 9y – 7 = 0

Example – 29:

A(5, -6), B(-1, 2) and C(4, -3) are three given points. Find the equation of locus of points P such that PA² – PB² = 12.

Solution:

Let P(x. y) be the point on the locus, Given A(5, -6), B(-1, 2) and C(4, -3) be the given points

Given  PA² – PB² = 12

∴ [(x – 5 )²  + (y + 6)² ] –  [(x + 1)²  + (y – 2)²] =12

∴ (x²  – 10x + 25 + y² + 12y + 36) – (x² + 2x + 1  + y² – 4y + 4) = 12

∴ x²  – 10x + 25 + y² + 12y + 36 – x² – 2x –  1  – y² + 4y – 4 – 12 = 0

∴ – 12x  + 16y  + 44 = 0

∴ 3x  – 4y  – 11 = 0

Hence required equation of the locus  is 3x  – 4y  – 11 = 0

Example – 30 :

Find the equation of locus of a point such that its distance from the origin is three times its distance from the x-axis.

Solution:

Let P(x. y) be the point on the locus, O(0. 0) be the origin

Distance of point from x-axis = y

Given: OP = 3y

∴ OP² = 9y²

∴ [(x – 0 )²  + (y – 0)² ] = 9y²

∴ x ²  + y ²  = 9y²

∴ x ²  –  8y ²  = 0

Hence required equation of the locus  is x ²  –  8y ²  = 0

Science > Mathematics > Coordinate Geometry > Locus > Equation of Locus