Science > Mathematics > Coordinate Geometry > Straight Lines > Intercepts of Line on the Axes
In this article, we shall study the concept of intercepts of line on coordinate axes.
If a straight line intercepts X-axis at the point A and Y-axis at point B, then the x-coordinate of A and y-coordinate of B are called x-intercept and y-intercept of the line on the axes respectively.
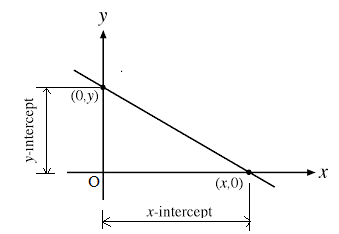
Generally, x-intercept is represented by letter ‘a’ and y-intercept is represented by letter ‘b’.
Example 01:
Find slopes and intercepts of the following lines.
- 3x + 4y = 12
Solution:
Equation of line is 3x + 4y – 12 = 0
Slope of line = – (coefficient of x/coefficient of y)
∴ Slope of line = – (3/4) = – 3/4
To find x-intercept of line substitute y = o in the equation of line
∴ 3x + 4 (0) -12 = 0
∴ 3x = 12
∴ x = 4
To find y-intercept of line substitute x = 0 in the equation of line
∴ 3(0) + 4 y -12 = 0
∴ 4y = 12
∴ y = 3
Ans: Slope of line = – 3/4, x-intercept = 4, and y-intercept = 3
- 2x + 3y = 6
Solution:
Equation of line is 2x + 3y – 6 = 0
Slope of line = – (coefficient of x/coefficient of y)
∴ Slope of line = – (2/3) = – 2/3
To find x-intercept of line substitute y = o in the equation of line
∴ 2x + 3(0) – 6 = 0
∴ 2x = 6
∴ x = 3
To find y-intercept of line substitute x = 0 in the equation of line
∴ 2(0) + 3y – 6 = 0
∴ 3y = 6
∴ y = 2
Ans: Slope of line = – 2/3, x-intercept = 3, and y-intercept = 2
- Y = 3x – 4
Solution:
Equation of line is 3x –y – 4 = 0
Slope of line = – (coefficient of x/coefficient of y)
∴ Slope of line = – (3/-1) = 3
To find x-intercept of line substitute y = o in the equation of line
∴ 3x – (0) – 4 = 0
∴ 3x = 4
∴ x = 4/3
To find y-intercept of line substitute x = o in the equation of line
∴ 3(0) – y -4 = 0
∴ – y = 12
∴ y = – 4
Ans: Slope of line = 3, x-intercept = 4/3, and y-intercept = – 4
- x/4 – y/3 = 2
Solution:
Equation of line is x/4 – y/3 = 2
Multiplying throughout by 12
∴ 3x – 4y = 24
∴ 3x – 4y – 24 = 0
Slope of line = – (coefficient of x/coefficient of y)
∴ Slope of line = – (3/-4) = 3/4
To find x-intercept of line substitute y = o in the equation of line
∴ 3x – 4(0) – 24 = 0
∴ 3x = 24
∴ x = 8
To find the y-intercept of line substitute x = o in the equation of line
∴ 3(0) – 4y – 24 = 0
∴ – 4y = 24
∴ y = – 6
Ans: Slope of line = 3/4, x-intercept = 8, and y-intercept = – 6
- x/2 – y/3 = 1/4
Solution:
Equation of line is x/2 – y/3 = 1/4
Multiplying throughout by 12
∴ 6x – 4y = 3
∴ 6x – 4y – 3 = 0
Slope of line = – (coefficient of x/coefficient of y)
∴ Slope of line = – (6/-4) = 3/2
To find x-intercept of line substitute y = o in the equation of line
∴ 6x – 4(0) – 3 = 0
∴ 6x = 3
∴ x = 1/2
To find y-intercept of line substitute x = o in the equation of line
∴ 6(0) – 4y – 3 = 0
∴ – 4y = 3
∴ y = – 3/4
Ans: Slope of line = 3/2, x-intercept = 1/2, and y-intercept = – 3/4
- 2x/3 + y/4 = 5
Solution:
Equation of line is 2x/3 + y/4 = 5
Multiplying throughout by 12
∴ 8x + 3y = 60
∴ 8x + 3y – 60 = 0
Slope of line = – (coefficient of x/coefficient of y)
∴ Slope of line = – (8/3) = – 8/3
To find x-intercept of line substitute y = o in the equation of line
∴ 8x + 3(0) – 60 = 0
∴ 8x = 60
∴ x = 60/8 = 15/2
To find y-intercept of line substitute x = o in the equation of line
∴ 8(0) + 3y – 60 = 0
∴ 3y = 60
∴ y = 20
Ans: Slope of line = – 8/3, x-intercept = 15/2, and y-intercept = 20
Example – 02:
Find the Slope of a line which makes equal intercepts on the axes.
Solution:
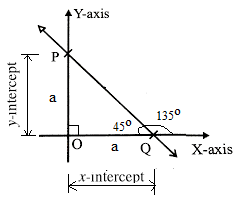
Let line PQ makes an equal intercepts on both the axes.
Thus in right-angled DPOQ, side OP = side OQ
Thus ΔPOQ is right angled isosceles triangle.
Thus m ∠ PQO = 45o
Thus line PQ makes an angle of 135o with the positive direction of x-axis
θ = 135o
Slope of line PQ = m = tan θ = tan 135o = -1
Thus the slope of a line making equal intercepts on coordinate axes is -1
Example – 03:
Find the Slope of a line which makes equal intercepts but of opposite signs on the axes.
Solution:

Let line PQ makes an equal but opposite in signs intercepts on both the axes.
Thus in right-angled DPOQ, side OP = side OQ
Thus DPOQ is right angled isosceles triangle.
Thus m ∠ PQO = 45o
Thus line PQ makes an angle of 45o with the positive direction of x-axis
θ = 45o
Slope of line PQ = m = tan θ = tan 45o = 1
Thus the slope of a line making equal but opposite in signs intercepts on coordinate axes is 1