Science > Mathematics > Pair of Straight Lines > Joint Equation of Lines When Lines are Parallel to Axes
In this article, we shall study to find a combined or joint equation of pair of lines when lines are parallel to coordinate axes.
Algorithm:
- When line passes through (h, k) and is parallel to co-ordinate axes are given. Equations of lines are x = h and y = k
- Write equations of lines in the form u = 0 and v = 0.
- Find u.v = 0.
- Simplify the L.H.S. of the joint equation.
Example 01:
- Find the joint equation of a pair of lines which passes through (1, 2) and parallel to co-ordinate axes.
- Solution:
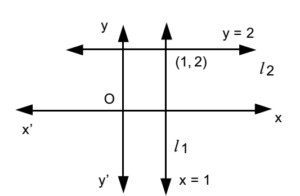
Let l1 and l2 be the two lines.
Equation of l1 passing through (1, 2) and parallel to y-axis is x = 1
∴ x – 1 = 0 …………. (1)
Equation of l2 passing through (1, 2) and parallel to x-axis is y = 2
∴ y – 2 = 0 …………. (2)
The required joint equation is
(x – 1)(y – 2) = 0
∴ xy – 2x – y + 2 = 0
This is the required combined equation.
Example 02:
- Find the joint equation of a pair of lines which passes through (-3, 4) and parallel to co-ordinate axes.
- Solution:
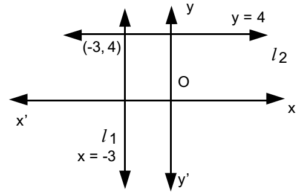
Let l1 and l2 be the two lines.
Equation of l1 passing through (-3, 4) and parallel to y – axis is x = -3
∴ x + 3 = 0 …………. (1)
Equation of l2 passing through (-3, 4) and parallel to x – axis is y = 4
∴ y – 4 = 0 …………. (2)
The required joint equation is
(x + 3)(y – 4) = 0
∴ xy – 4x + 3y – 12 = 0
This is the required combined equation.
Example 03:
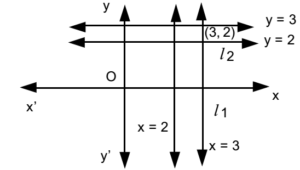
- Find the joint equation of a pair of lines which passes through (3, 2) and parallel to the lines x = 2 and y = 3.
- Solution:

Let l1 and l2 be the two lines.
Equation of l1 passing through (3, 2) and parallel to x = 2 is x = 3
∴ x – 3 = 0 …………. (1)
Equation of l2 passing through (3, 2) and parallel to y = 3 is y = 2
∴ y – 2 = 0 …………. (2)
The required joint equation is
(x – 3)(y – 2) = 0
∴ xy – 2x – 3y + 6 = 0
This is the required combined equation.
Example 04:
- Find the joint equation of a pair of lines which passes through (2, 3) and parallel to co-ordinate axes.
- Solution:

Let l1 and l2 be the two lines.
Equation of l1 passing through (1, 2) and parallel to y – axis is x = 2
∴ x – 2 = 0 …………. (1)
Equation of l2 passing through (1, 2) and parallel to x – axis is y = 3
∴ y – 3 = 0 …………. (2)
The required joint equation is
(x – 2)(y – 3) = 0
∴ xy – 3x – 2y + 6 = 0
This is the required combined equation.
Example 05:
- Find the joint equation of a pair of lines which are at a distance of 9 units from the y-axis and parallel to it.
- Solution:

Let l1 and l2 be the two lines.
Equation of l1 which is at a distance of 9 from y – axis and parallel to it is x = – 9 i.e. x + 9 = 0 …. (1)
Equation of l2 which is at a distance of 9 from y – axis and parallel to it is x = 9 i.e. x – 9 = 0 …… (1)
The required joint equation is
(x + 9)(x – 9) = 0
∴ x2 – 81 = 0
This is the required combined equation.
Example 06:
- Find the joint equation of a pair of lines which are at a distance of 5 units from the x-axis and parallel to it.
- Solution:

Let l1 and l2 be the two lines.
Equation of l1 which is at a distance of 5 from x – axis and parallel to it is y = 5i.e. y – 5 = 0 ……… (1)
Equation of l2 which is at a distance of 5 from x – axis and parallel to it is y = -5 i.e. y + 5 = 0 …… (2)
The required joint equation is
(y – 5)(y + 5) = 0
∴ y2 – 25 = 0
This is the required combined equation.